Construction / Practical Geometry (basics) : Fundamental Elements of Practical Geometry

maths > construction-basics

Fundamental Elements of Practical Geometry

what you'll learn...

overview

The four fundamental elements of Practical Geometry are explained.

  1. Constructing co-linear points.

  2. Constructing equi-distant points

  3. Constructing equi-angular points

  4. Constructing parallel points.

Constructing a Line

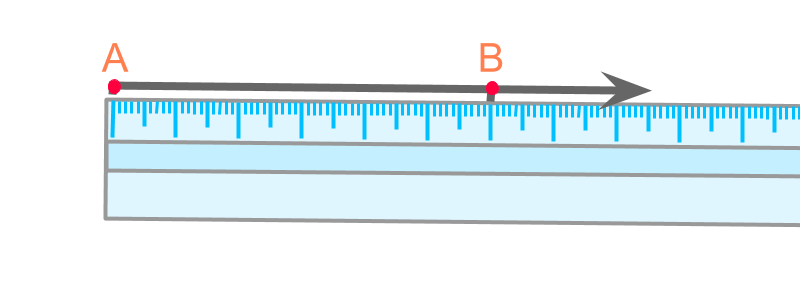
A ruler helps to construct a line through two points.

The points on a line are called "collinear points".

The word "collinear" means: of lying in the same line.

"co" means "together; jointly" ; and "linear" means "line".

summary

Constructing a Line through two Points: Connect two points using a ruler or a scale and extend in both the directions.

Constructing an Arc

A "compass" helps to construct an arc at a distance $5$ $5$ cm from point $A$ $A$ .

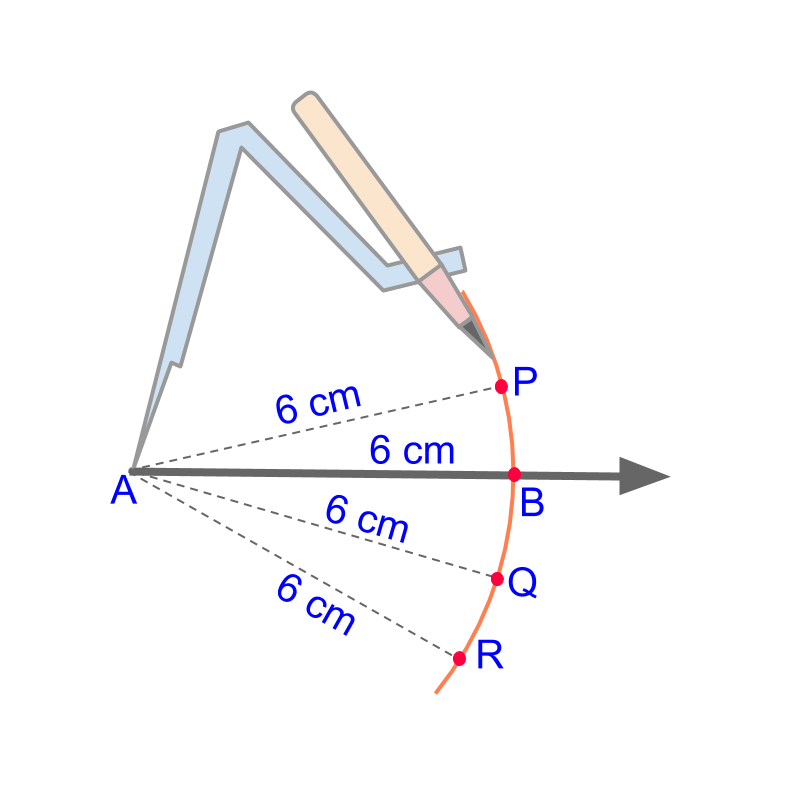
The points on an arc are called "equidistant points".

The word "equidistant" means: at equal distance.

The points $P$ $P$ , $B$ $B$ , $Q$ $Q$ , and $R$ $R$ are at the equal distant from the point $A$ $A$ .

summary

Constructing an arc : Measure the distance using a compass and mark the arc at the distance from the point.

Constructing an Angle

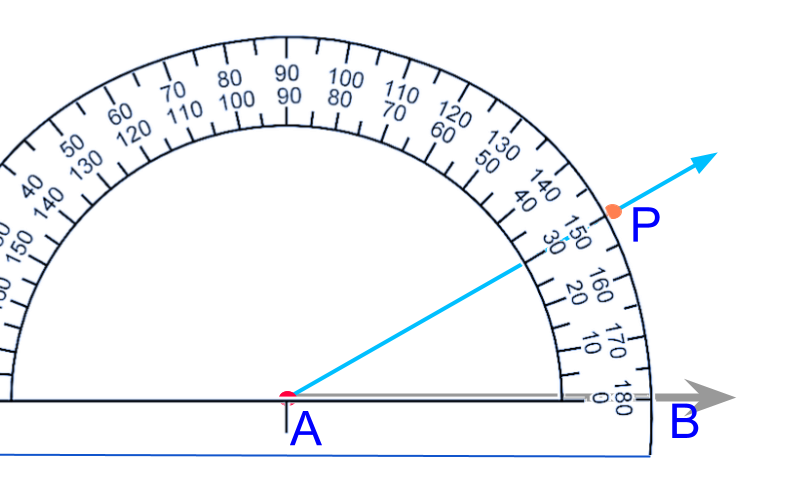
A protractor helps to mark an angle of a given measure.

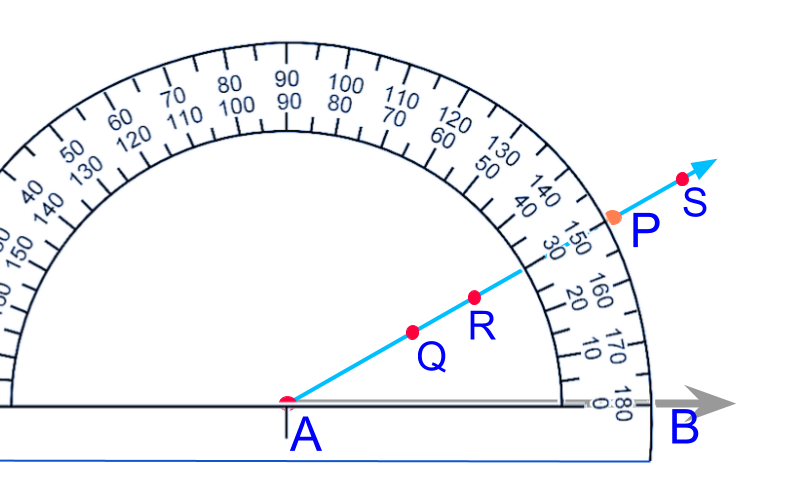
The points on the ray at an angle to $bar(AB)$ are called equiangular points to the line.

The word "equiangular" means: having equal angle.

summary

Constructing a given Angle : Using a protractor measure the given angle and extend the ray.

Constructing a Parallel to a given line

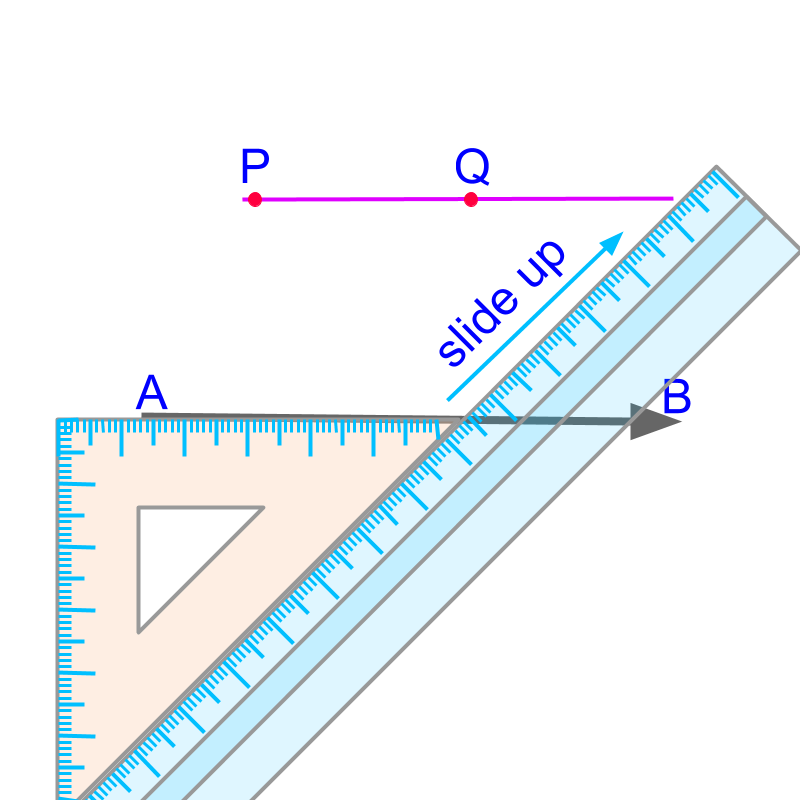
Set-squares or set-triangles help to construct a parallel to a given line.

The word "parallel" means: lines having same distance continuously between them.

summary

Constructing a Parallel : Set a leg of the set-square on a line and slide the set-square along its diagonal. The parallel can be constructed on the leg.

fundamental elements

In practical geometry, we study about constructing

• line segments,

• angles

that make different plane-figures like triangles, rectangles, quadrilaterals, etc. The following are the fundamental elements to practical geometry.

   constructing a line (collinear points),

   Constructing an arc (equidistant points),

   Constructing an angle or (equiangular points), and

   Constructing a parallel (parallel points)

The fundamental elements of practical geometry are

  1. constructing a straight line using a ruler (which are points collinear to two points).

  2. measuring a distance using a compass and marking an arc (which are points equidistant to the center).

  3. measuring an angle using a protractor and marking a ray with the angle (which are points equiangular to the initial point)

  4. constructing a parallel using set squares (which are points on a line parallel to a given line)

In the course of the lessons, the secondary elements and the end-applications will be explained. For example, bisecting a line or constructing a parallel line using a compass are some examples of secondary elements. The primary elements are used to construct the secondary elements.

And, constructing a square using the length of a diagonal or constructing a parallelogram are some examples of end-applications. These constructions use combination of primary and secondary elements.

summary

Fundamental Elements of Practical Geometry :

  1. Constructing a line connecting $2$ points using a scale or ruler: Constructing co-linear points.

  2. Constructing an arc of given radius with a compass : Constructing equi-distant points

  3. Constructing an angle of given measure with a protractor : Constructing equi-angular points

  4. Constructing a parallel at a given distance to a line : Constructing parallel points.

Outline