
what you'll learn...
overview
In this page, constructing the following using a compass are explained.
• 60∘60∘ angle
• 30∘30∘ angle
• 120∘120∘ angle
• 15∘15∘ angle
• 90∘90∘ angle
Constructing 60∘ angle using Compass
We know that, Angles in a equilateral triangle are 60∘. This geometrical property helps to construct 60∘ angle using a compass.
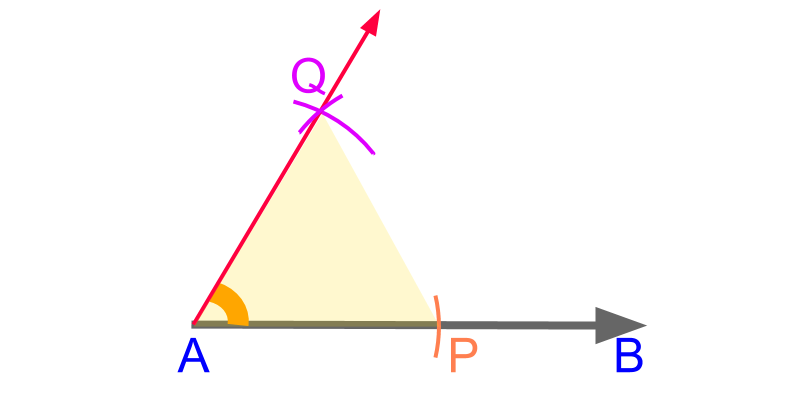
To construct an angle measuring 60∘ at point A on line ¯AB, construct a equilateral triangle as given below.
• With an arbitrary distance measure on compass, mark point P from point A on line ¯AB.
• With the same distance measure on compass, construct two arcs from points A and P. The arcs cut at point Q.
Since the distance measure on compass is identical, points A, P, and Q make an equilateral triangle. The line ¯AQ is extended and ∠PAQ is 60∘
Constructing 60∘ angle using a Compass : Construct an equilateral triangle and the angle 60∘ is constructed at the vertex.
Constructing 30∘ angle using Compass
To construct 30∘ angle using a compass, we use the property that 30∘ is half of 60∘.
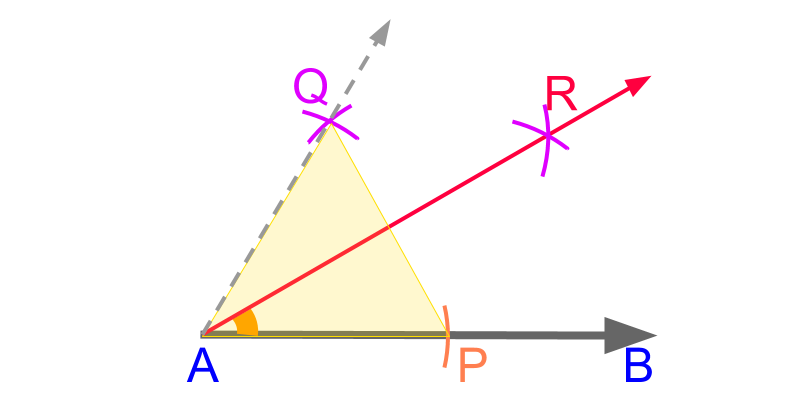
We have learned constructing 60∘ and bisecting an angle using a compass. Combine these two to construct 30∘ angle.
• With an arbitrary distance-measure on compass, mark point P from point A on line ¯AB.
• With the same distance measure on compass, construct two arcs from points A and P. The arcs cut at point Q. ¯AQ makes 60∘ with the ¯AP.
• With an arbitrary distance-measure on compass, construct two arcs from points P and Q. These arcs cut at point R. The line ¯AR bisects the angle ∠PAQ.
The angle 30∘ is constructed as ∠PAR.
Constructing 30∘ angle using a Compass : Construct an equilateral triangle and the angle 60∘ is constructed at the vertex. Bisect the angle.
Constructing 120∘ angle using Compass
To construct 120∘ angle using a compass, we use the property that 120∘ is double of 60∘.
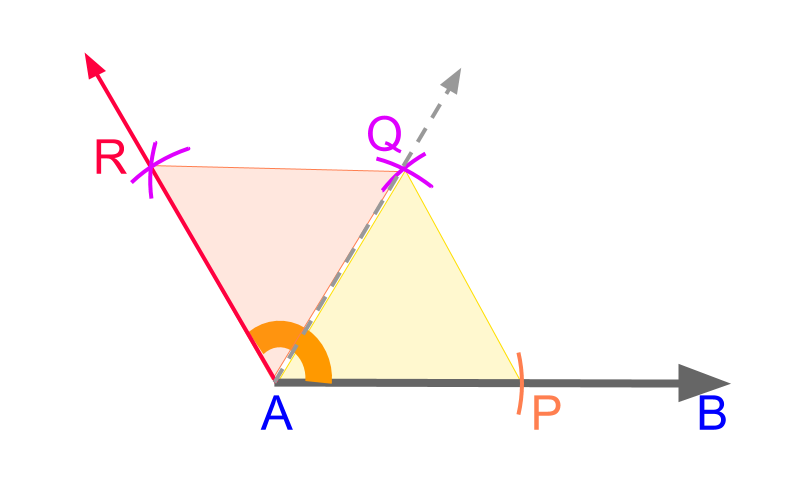
Constructing 60∘ angle twice-over to construct 120∘
• With an arbitrary distance-measure on compass, mark point P from point A on line ¯AB.
• With the same distance measure on compass, construct two arcs from points A and P. The arcs cut at point Q. ¯AQ makes 60∘ with the ¯AP.
• With the same distance measure on compass, construct two arcs from points A and Q. The arcs cut at point R. ¯AR makes 120∘ with the ¯AP.
The angle 120∘ is constructed as ∠PAR.
Constructing 120∘ angle using a Compass : Construct an equilateral triangle and another equilateral triangle on the side of the constructed one.
Constructing 15∘ angle using Compass
To construct 15∘ angle using a compass, we use the property that 15∘ is half of 30∘.
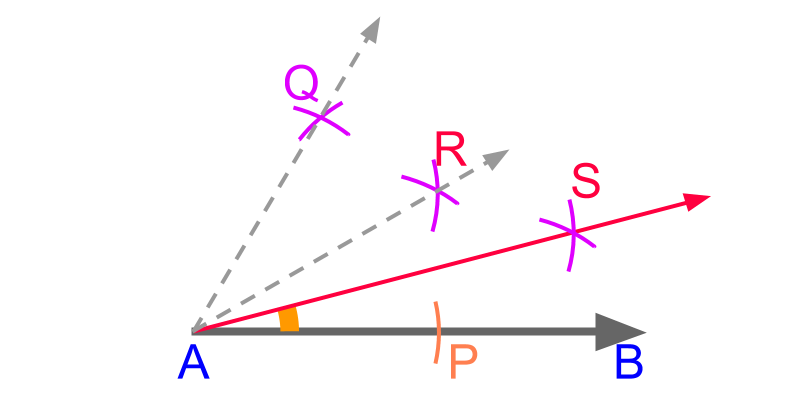
We have learned constructing 60∘ and bisecting an angle using a compass. Combine these two to construct 15∘ angle.
• With an arbitrary distance-measure on compass, mark point P from point A on line ¯AB.
• With the same distance measure on compass, construct two arcs from points A and P. The arcs cut at point Q. ¯AQ makes 60∘ with the ¯AP.
• With an arbitrary distance-measure on compass, construct two arcs from points P and Q. These arcs cut at point R. The line ¯AR bisects the angle ∠PAQ.
• With an arbitrary distance-measure on compass, construct two arcs from points P and R. These arcs cut at point S. The line ¯AS bisects the angle ∠PAS.
The angle 15∘ is constructed as ∠PAS.
Constructing 15∘ angle using a Compass : Construct an equilateral triangle and the angle 60∘ is constructed at the vertex. Bisect the angle twice.
Constructing 90∘ angle using Compass
To construct 90∘ angle using a compass, we use the property that 90∘ is sum of 60∘ and 30∘.

Constructing 90∘ with two 60∘ is illustrated
• With an arbitrary distance-measure on compass, mark point P from point A on line ¯AB.
• With the same distance measure on compass, construct two arcs from points A and P. The arcs cut at point Q. ¯AQ makes 60∘ with the ¯AP.
• With the same distance measure on compass, construct two arcs from points A and Q. The arcs cut at point R. ¯AR makes 120∘ with the ¯AP.
• With an arbitrary distance-measure on compass, construct two arcs from points Q and R. These arcs cut at point S. The line ¯AS bisects the angle ∠QAR.
The angle 90∘ is constructed as ∠PAS.
Constructing 90∘ angle using a compass : Construct two equilateral triangles and bisect the second one to construct 90∘ angle.
summary
Constructing 60∘ angle using a Compass : Construct an equilateral triangle and the angle 60∘ is constructed at the vertex.
Constructing 30∘ angle using a Compass : Construct an equilateral triangle and the angle 60∘ is constructed at the vertex. Bisect the angle.
Constructing 120∘ angle using a Compass : Construct an equilateral triangle and another equilateral triangle on the side of the constructed one.
Constructing 15∘ angle using a Compass : Construct an equilateral triangle and the angle 60∘ is constructed at the vertex. Bisect the angle twice.
Constructing 90∘ angle using a compass : Construct two equilateral triangles and bisect the second one to construct 90∘ angle.
Outline
The outline of material to learn "Construction / Practical Geometry at 6-8th Grade level" is as follows.
Note: click here for detailed outline of "constructions / practical geometry".
• Four Fundamenatl elements
→ Geometrical Instruments
→ Practical Geometry Fundamentals
• Basic Shapes
→ Copying Line and Circle
• Basic Consustruction
→ Construction of Perpendicular Bisector
→ Construction of Standard Angles
→ Construction of Triangles
• Quadrilateral Forms
→ Understanding Quadrilaterals
→ Construction of Quadrilaterals
→ Construction of Parallelograms
→ Construction of Rhombus
→ Construction of Trapezium
→ Construction of Kite
→ Construction of Rectangle
→ Construction of Square