Construction / Practical Geometry (basics) : Construction of Rectangles

maths > construction-basics

Construction of Rectangles

what you'll learn...

overview

In this page, constructing rectangles is explained. It is outlined as follows.

• Properties of rectangles is explained

• The number of independent parameters in a rectangle is $1$ $1$

• For a given parameter, construction of rectangles is approached as combination of triangles (sss, sas, asa, rhs, sal) and using the properties of rectangles.

understanding rectangle

A rectangle is a parallelogram with all interior angles $90^{\circ}$ $90^@$

A quadrilateral is defined by $5$ $5$ parameters. A Parallelogram is defined by $3$ $3$ parameters. And for a rectangle, the following properties provide additional dependency of parameters.

• all interior angles are $90^{\circ}$ $90^@$

• diagonals are equal and bisect

• opposite sides are parallel and equal

• two angles on diagonals are supplementary.

These properties cause one parameter to be dependent on other parameters and so, a rectangle is defined by $2$ $2$ parameters.

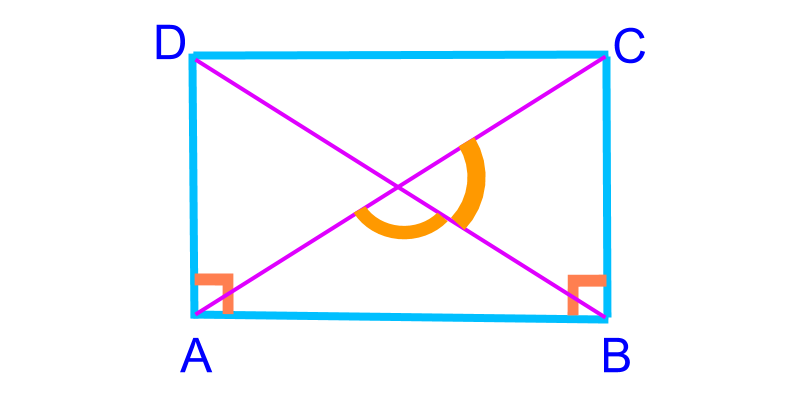
To construct a rectangle, $2$ sides ( $bar(AB)$ , $bar(BC)$ ) are given. This is illustrated in the figure. To construct, consider this as two SAS triangles $ABC$ and $ABD$ .

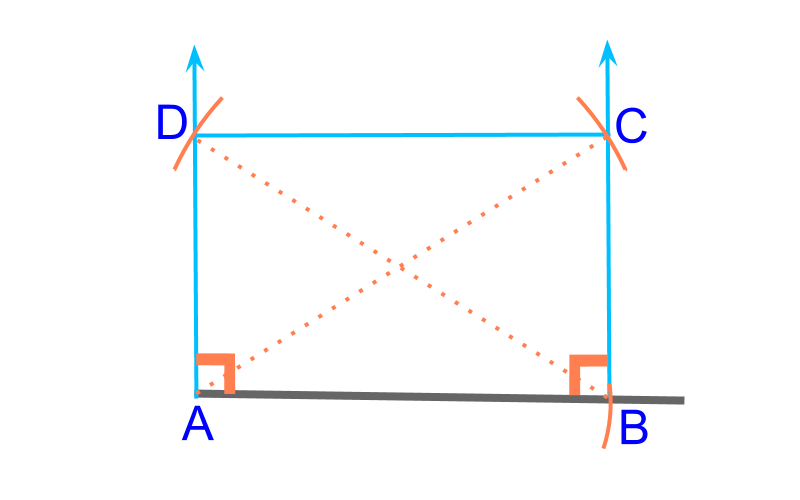
rectangle construction a side and the diagonal

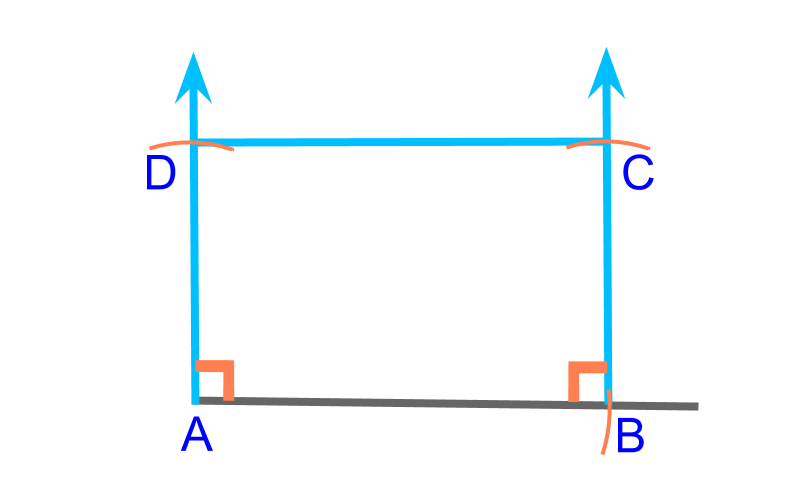
To construct a rectangle, a side ( $bar(AB)$ ) and the diagonal ( $bar(AC)$ ) are given. This is illustrated in the figure. To construct, consider this as two RHS triangles $ABC$ and $ABD$ .

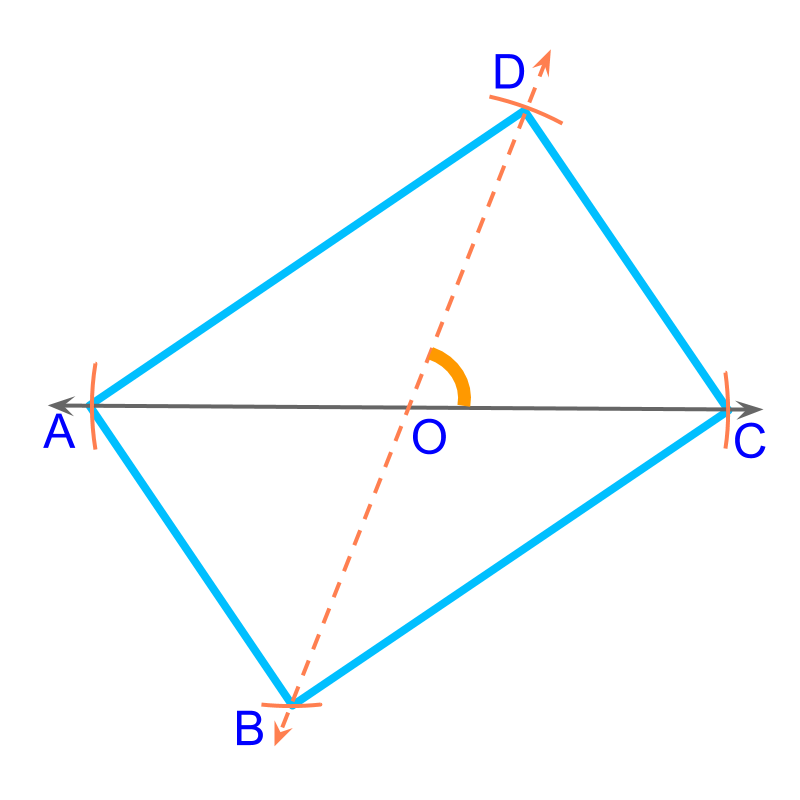
To construct a rectangle, the diagonal ( $bar(AC)$ ) and the angle between them ( $/_DOC$ ) are given. This is illustrated in the figure.

To construct the specified rectangle, "Consider this as two SAS triangle $COD$ and $AOB$ ". Note: Use the property that diagonals bisect and mark the vertices at half diagonals.

summary

Construction of Rectangles :

Properties of rectangle

• all interior angles are $90^@$

• diagonals are equal and bisect

• opposite sides are parallel and equal

The formulations of questions

• $2$ sides

• $1$ side and the diagonal

• the diagonal and an angle between the diagonals

use properties to figure out dependent parameters and look for triangles

Outline