Calculus - Limit : Understanding limits with the graph of the function

maths > calculus-limits

Understanding limits with the graph of the function

what you'll learn...

Understanding Limits with Graph of the function

» Values of Function at $x = a$ $x=a$
limit x=a     → Evaluated at input $f (x) ∣_{x = a}$ $f(x)|_(x=a)$ or $f (a)$ $f(a)$

    → Left-hand-limit $lim x \to a - f (x)$ $lim_(x->a-) f(x)$

    → Right-hand-limit $lim x \to a + f (x)$ $lim_(x->a+) f(x)$

In the previous pages, limit is defined in algebraic form.

In this topic, the function is considered as a graph in a 2D coordinate plane and the meaning of limit is explained.

example

The value of $f (x) = \frac{x^{2} - 1}{x - 1}$ $f(x) = color(deepskyblue)(x^2-1)/color(coral)(x-1)$ when $x=1$ is $0/0$ .

On substituting $x=1$ , we get $f(1)= 0/0$ .

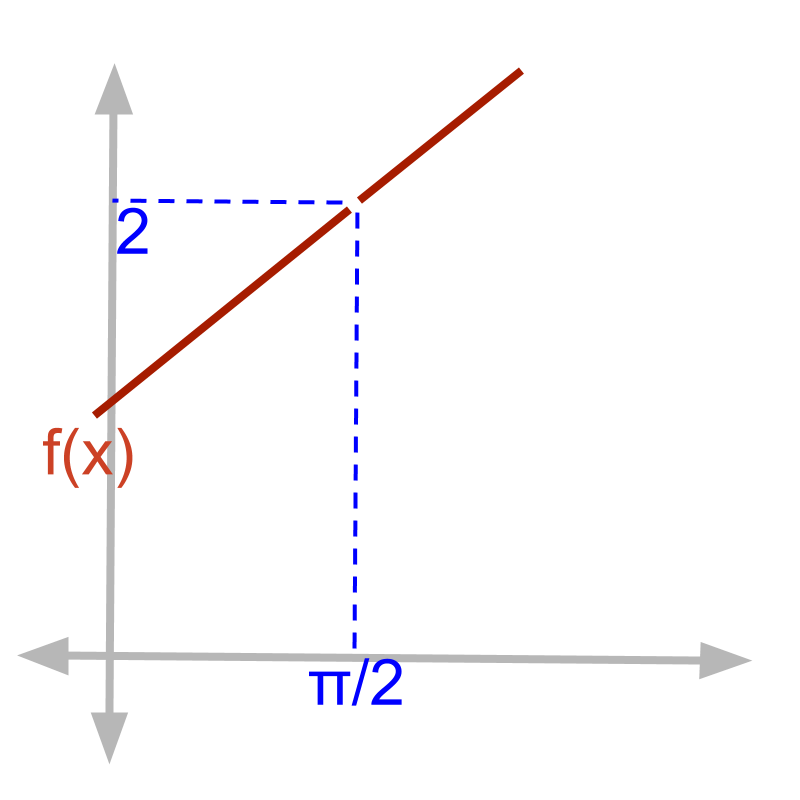
The plot of $f(x) = color(deepskyblue)(x^2-1)/color(coral)(x-1)$ is shown.

At $x=1$ , the graph breaks and the function does not evaluate to a real number.

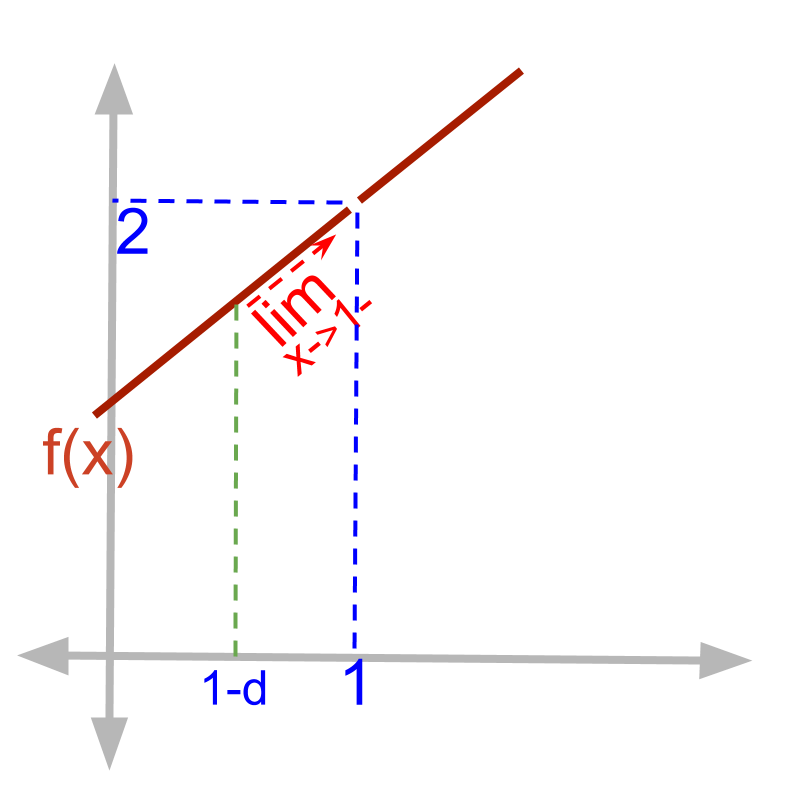
Left-hand-limit of $f(x) = color(deepskyblue)(x^2-1)/color(coral)(x-1)$ is shown.

At $x=1-delta$ , dotted vertical line is shown.

Applying limit is moving the vertical line towards $x=1$ and making $delta~=0$ . This is shown as $lim_(x->1-)$ in the figure.

$lim_(x->1-)f(x)$
$quad quad = color(deepskyblue)((1-delta)^2-1)/color(coral)((1-delta)-1)$
$quad quad = color(deepskyblue)(1-2delta+delta^2-1)/color(coral)(1-delta-1)$
$quad quad = color(deepskyblue)(-delta(2-delta)) /color(coral)(-delta)$
$quad quad = 2-delta$
$quad quad = 2$ (substituting $delta=0$ )

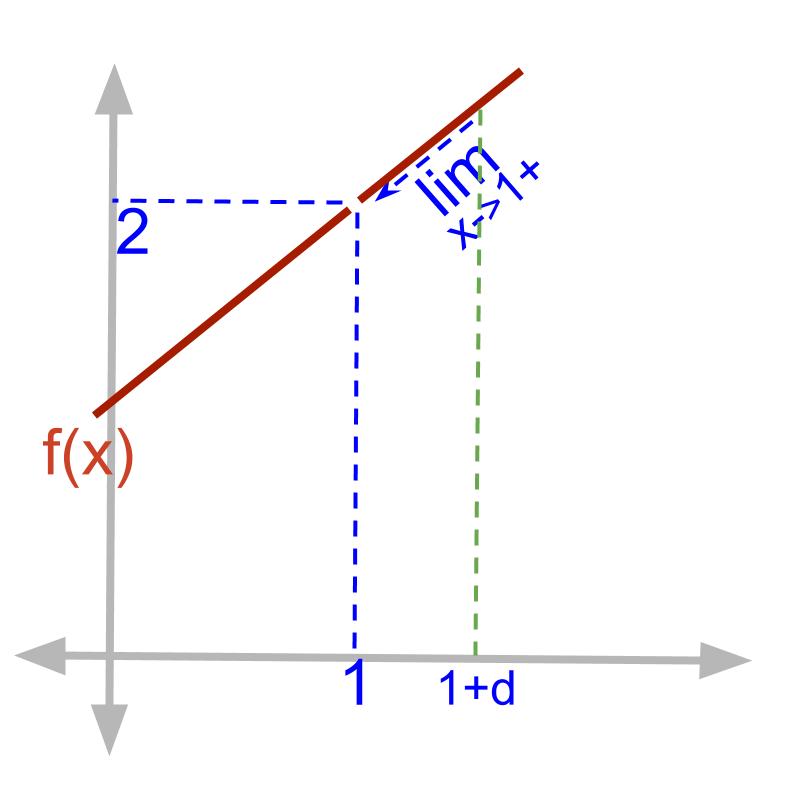
Right-hand-limit of $f(x) = color(deepskyblue)(x^2-1)/color(coral)(x-1)$ is shown.

At $x=1+delta$ , dotted vertical line is shown.

Applying limit is moving the vertical line towards $x=1$ and making $delta~=0$ . This is shown as $lim_(x->1+)$ in the figure.

$lim_(x->1+)f(x)$
$quad quad = color(deepskyblue)((1+delta)^2-1)/color(coral)((1+delta)-1)$
$quad quad = color(deepskyblue)(1+2delta+delta^2-1)/color(coral)(1+delta-1)$
$quad quad = color(deepskyblue)(delta(2+delta)) /color(coral)(delta)$
$quad quad = 2+delta$
$quad quad = 2$ (substituting $delta=0$ )

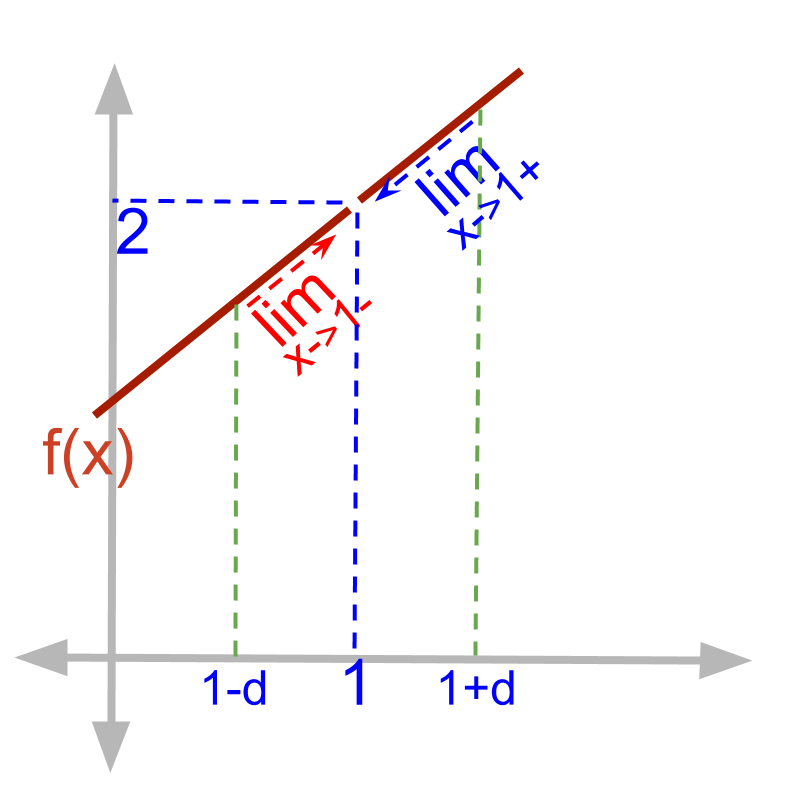
Both the limits of $f(x) = color(deepskyblue)(x^2-1)/color(coral)(x-1)$ is shown.

The right-hand-limit and left-hand-limits converge to $2$ .

Limit of a function at $x=a$ is understood as the value of function at $x=a$ , left side of that : $x=a-delta$ , and right side of that : $x=a+delta$

summary

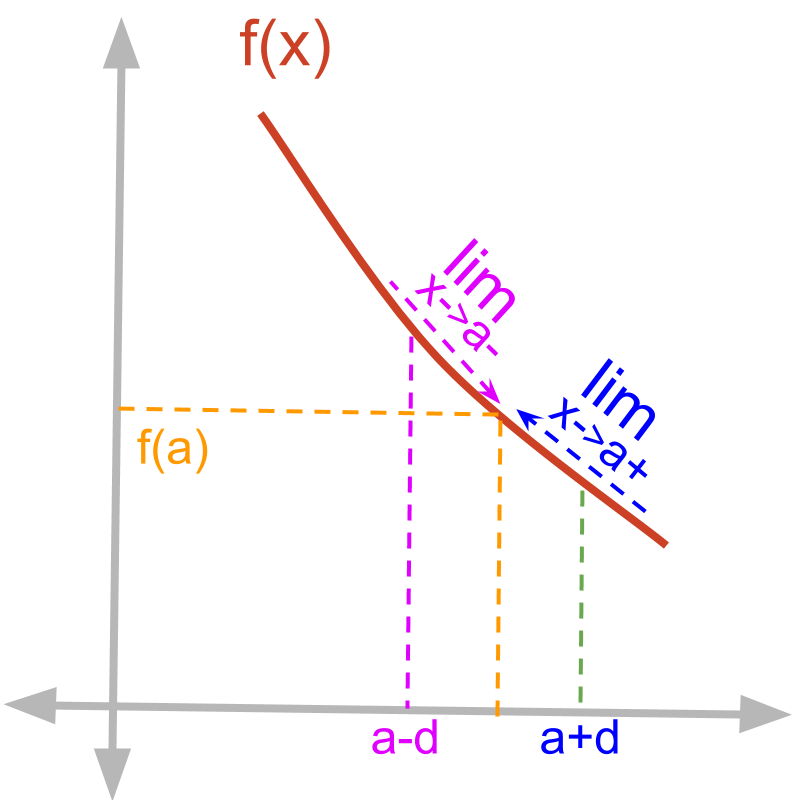
Limits of a function at $x=a$ are illustrated in the figure.

• Evaluated at input $f(x)|_(x=a)$ or $f(a)$
• Left-hand-limit $lim_(x->a-) f(x)$
• Right-hand-limit $lim_(x->a+) f(x)$

Outline

The outline of material to learn "limits (calculus)" is as follows.

Note : click here for detailed outline of Limits(Calculus).

→ Indeterminate and Undefined

→ Indeterminate value in Functions

→ Expected Value

→ Continuity

→ Definition by Limits

→ Geometrical Explanation for Limits

→ Limit with Numerator and Denominator

→ Limits of Ratios - Examples

→ L'hospital Rule

→ Examining a function

→ Algebra of Limits

→ Limit of a Polynomial

→ Limit of Ratio of Zeros

→ Limit of ratio of infinities

→ limit of Binomial

→ Limit of Non-algebraic Functions