Calculus - Limit : Understanding Limits : Examples

maths > calculus-limits

Understanding Limits : Examples

what you'll learn...

Limits by Numerator and Denominator

Slopes of the numerator and denominator at the point $x = a$ $x=a$ decide the limits of $f (x)$ $f(x)$ at $x = a$ $x=a$ .
» eg: $f (x) = \frac{2 x - 4}{x - 2}$ $f(x) = color(deepskyblue)(2x-4)/color(coral)(x-2)$
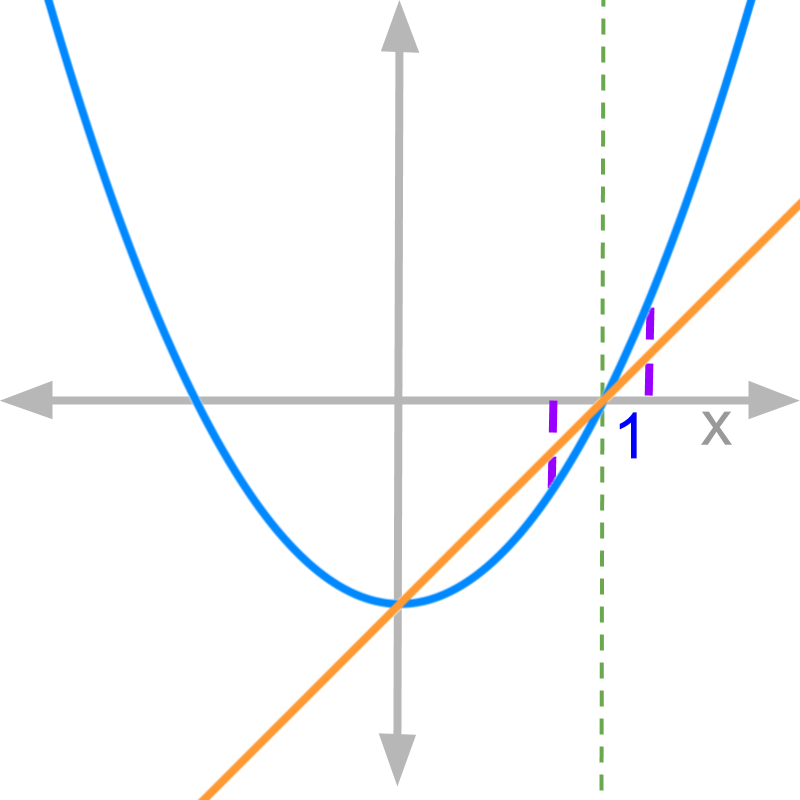limit x=a     → slope of numerator at $x = 2$ $x=2$ is $2$ $2$

    → slope of denominator at $x = 2$ $x=2$ is $1$

    → Both LHL and RHL limits $=2/1 = 2$

linear slopes

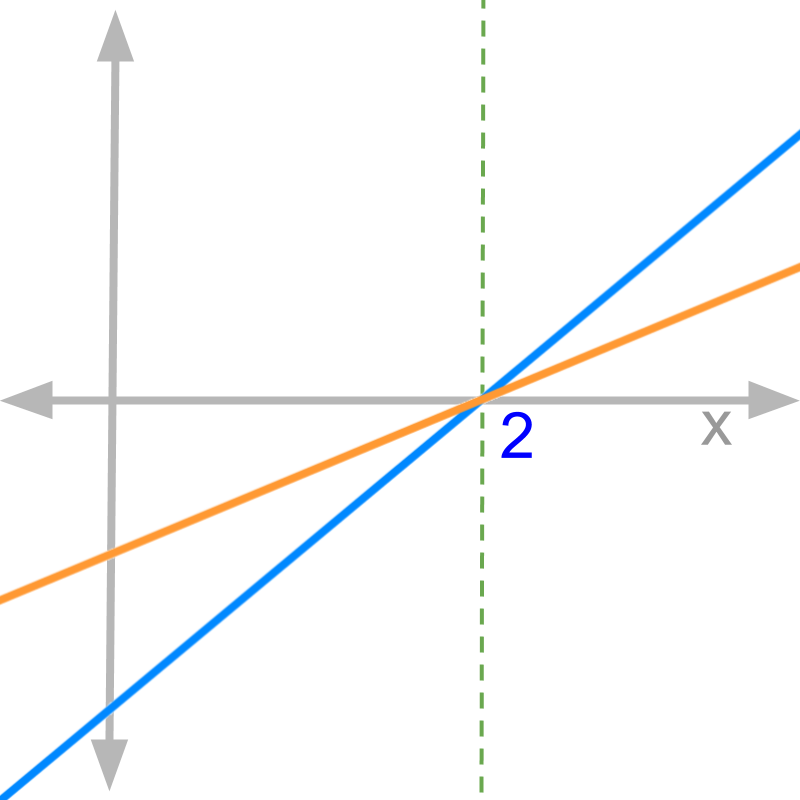
Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ .

The value of $lim_(x->2) f(x)>1$ . This is because, the slope of numerator is greater than the denominator.

The function given is $f(x) = color(deepskyblue)(2x-4)/color(coral)(x-2)$ . The slope of the numerator is $2$ and slope of the denominator is $1$ .

Left-hand-limit $x=2-delta$ of
$color(deepskyblue)(2x-4)/color(coral)(x-2)$
$quad quad = color(deepskyblue)(2(2-delta)-4)/color(coral)(2-delta-2)$
$quad quad = color(deepskyblue)(4-2delta-4)/color(coral)(-delta)$
$quad quad = color(deepskyblue)(-2delta)/color(coral)(-delta)$
$quad quad = 2$

Similarly, the right-hand-limit can be worked out to $2$ .

negative slope

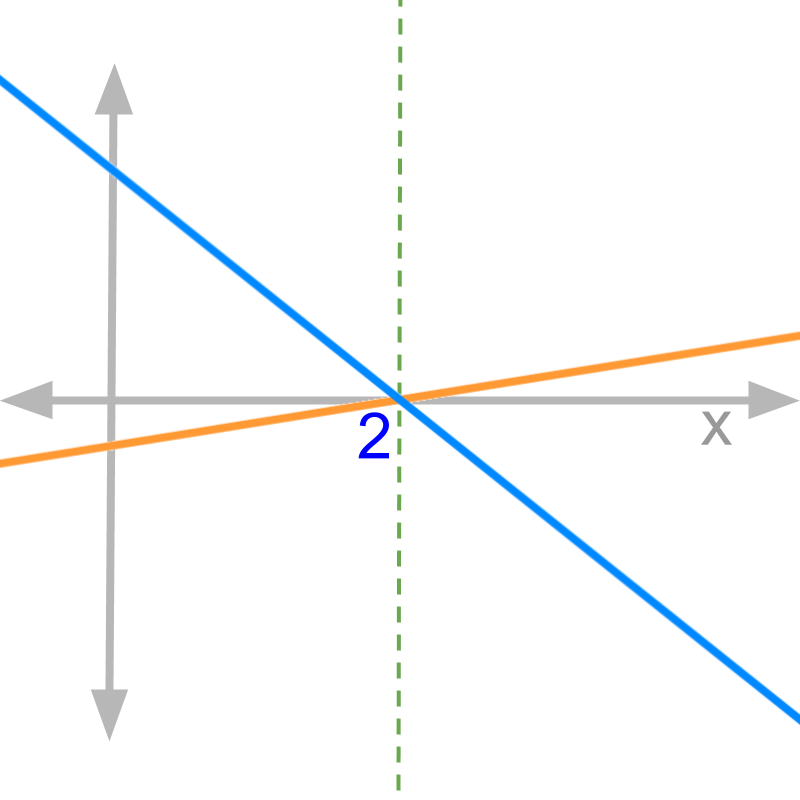
Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ .

The value of $lim_(x->2) f(x) < -1$ . This is because, the slope of the numerator is negative and decreasing steeper than the denominator.

The function given is $f(x) = color(deepskyblue)(6-3x)/color(coral)(.5x-1)$ . The slope of the numerator is $-3$ and the slope of the denominator is $0.5$ .

Right-hand-limit $x=2+delta$
$color(deepskyblue)(6-3(2+delta))/color(coral)(0.5(2+delta)-1)$
$quad quad = color(deepskyblue)(-3delta)/color(coral)(0.5delta)$
$quad quad = -6$

Similarly, left hand limit can be worked out as $-6$ .

same slopes

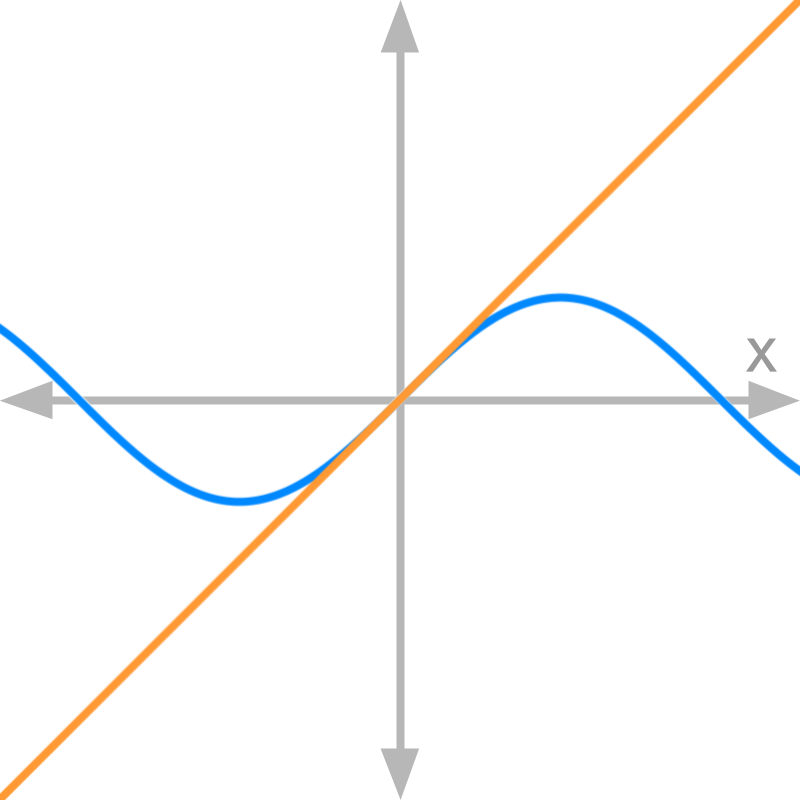
Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ .

The value of $lim_(x->0) f(x) = 1$ . This is because, the slope of the numerator equals that of the denominator at the given point.

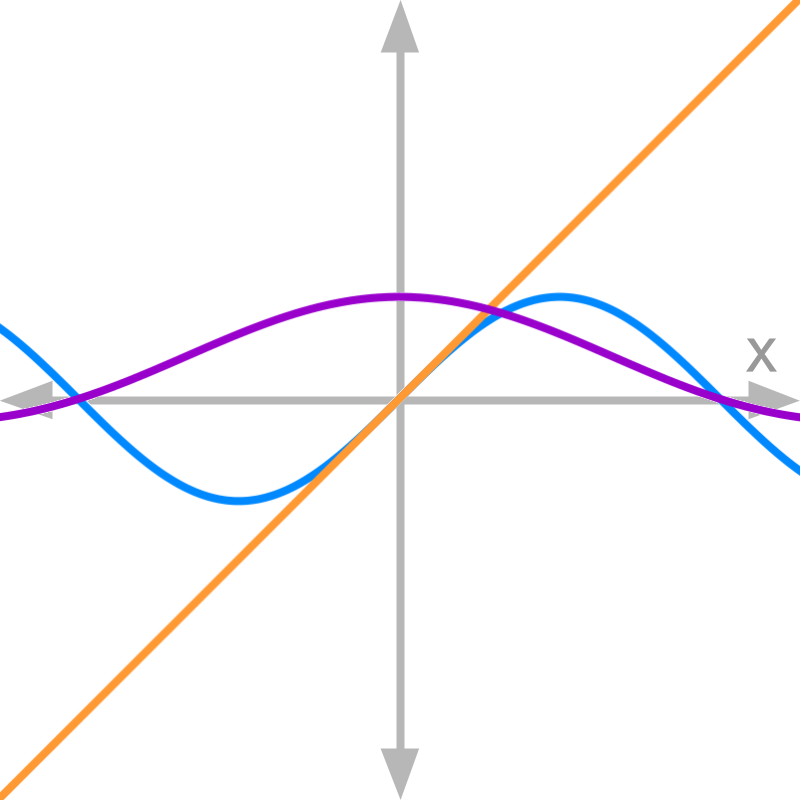
Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ (in purple).

The function given is $color(purple)(f(x)) = color(deepskyblue)(sin x)/color(coral)(x)$ . At $x=0$ the slope of the numerator is $1$ and slope of the denominator is $1$ .

Proof for limit of this function is explained later.

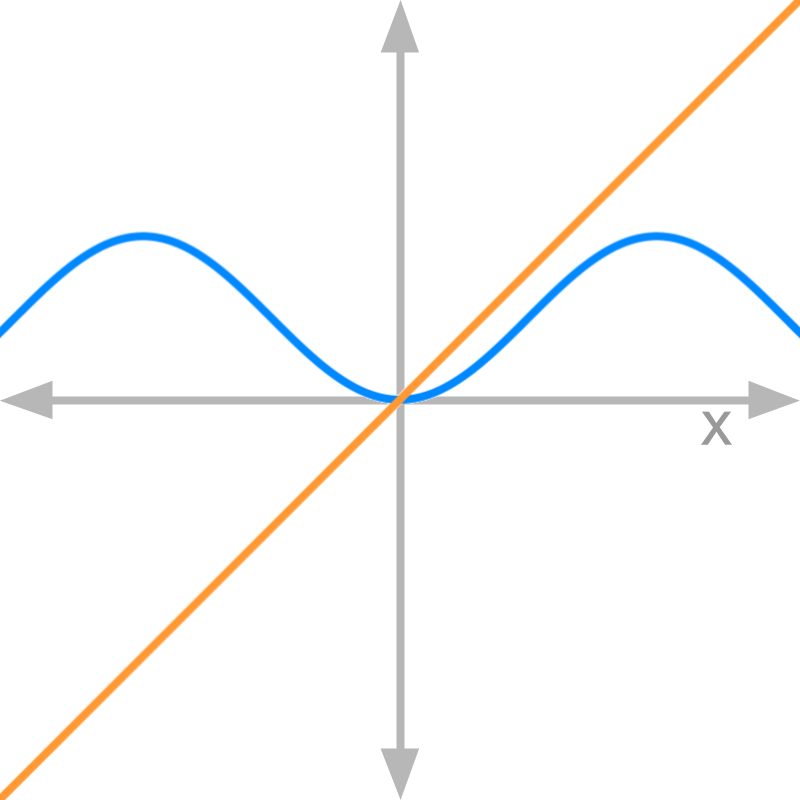
Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ .

The value of $lim_(x->0) f(x)=0$ . This is because, the slope of the numerator is $0$ and that of the denominator is $1$ .

slope = 0

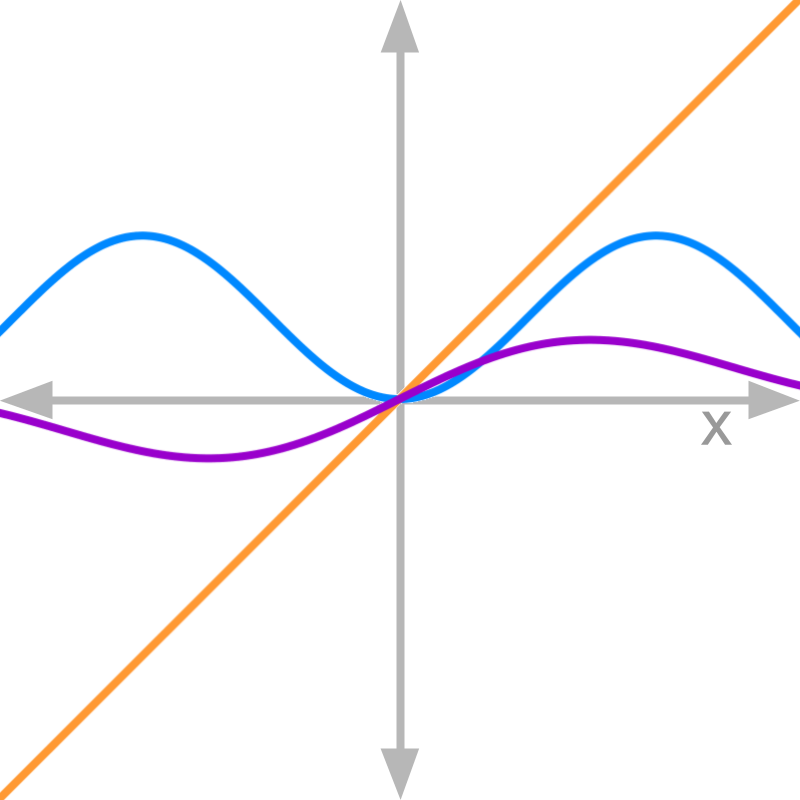
Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ (in purple).

The function given is $f(x) = color(deepskyblue)(1- cos x)/color(coral)(x)$ . The slope of the numerator is $0$ and the slope of the denominator is $1$ .

Proof for limit of this function is explained later.

don't analyse with limit

Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ .

The value of $lim_(x->0+) f(x)=oo$ . This function is not a candidate to analyze numerator and denominator, as the function does not evaluate to $0/0$ form.

don't limit

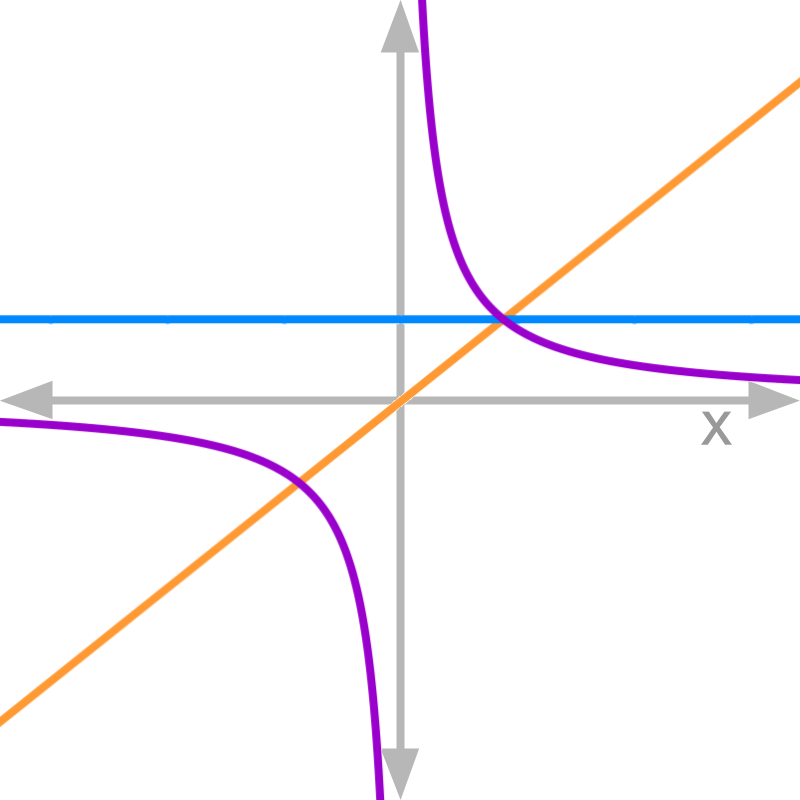
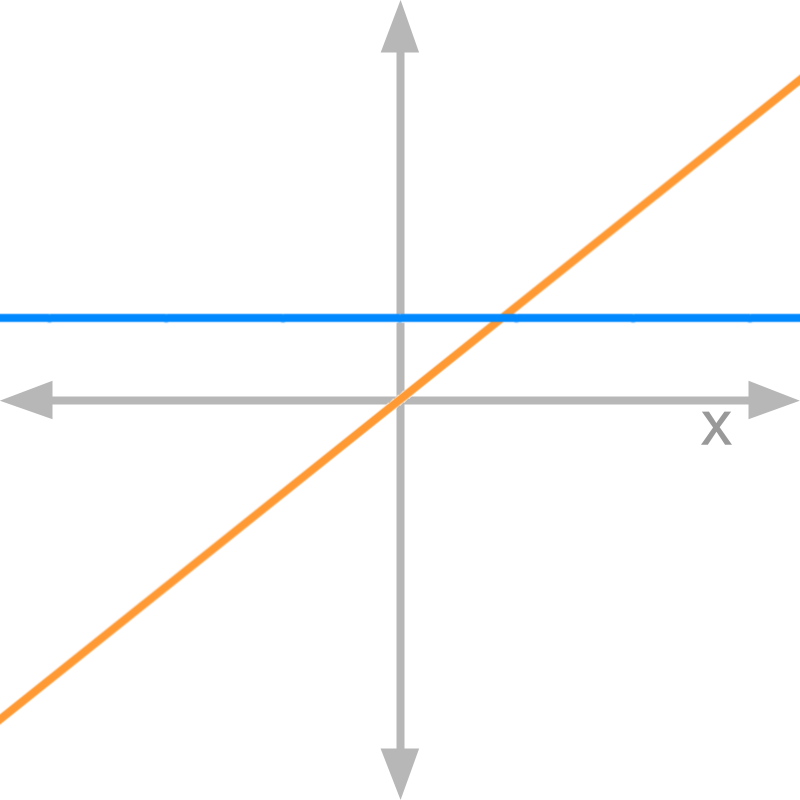
Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ (in purple).

The function given is $f(x) = color(deepskyblue)(1)/color(coral)(x)$ .
This function does not satisfy the pre-condition that numerator and denominator has to evaluate to $0$ . So the analysis by comparing slopes is not applicable.

example

Consider the graphs of numerator (in blue) and denominator (in orange) of function $f(x)$ .

The answer is ' $0$ '. The slope of numerator is $0$ and that of the denominator is $1$ .

summary

Slopes of the numerator and denominator at the point $x=a$ decide the limits of $f(x)$ at $x=a$ .
» eg: $f(x) = color(deepskyblue)(2x-4)/color(coral)(x-2)$
limit x=a     → slope of numerator at $x=2$ is $2$

    → slope of denominator at $x=2$ is $1$

    → Both LHL and RHL limits $=2/1 = 2$

Outline

The outline of material to learn "limits (calculus)" is as follows.

Note : click here for detailed outline of Limits(Calculus).

→ Indeterminate and Undefined

→ Indeterminate value in Functions

→ Expected Value

→ Continuity

→ Definition by Limits

→ Geometrical Explanation for Limits

→ Limit with Numerator and Denominator

→ Limits of Ratios - Examples

→ L'hospital Rule

→ Examining a function

→ Algebra of Limits

→ Limit of a Polynomial

→ Limit of Ratio of Zeros

→ Limit of ratio of infinities

→ limit of Binomial

→ Limit of Non-algebraic Functions