
what you'll learn...
Examining Function at an input Value
» A function f(x) at x=a is
→ continuous: if f(a) = LHL = RHL
→ defined by value: if f(a) is a real number
→ defined by limit: if f(a)=00 and LHL = RHL
→ not defined: if LHL ≠ RHL and f(a)∉ℝ
Limit of a Continuous Function
» A function f(x) at x=a is
 → continuous: if f(a) = LHL = RHL
→ continuous: if f(a) = LHL = RHL
Limit of a defined Function
» A function f(x) at x=a is
 → defined by limit: if f(a)=00 and LHL = RHL
→ defined by limit: if f(a)=00 and LHL = RHL
Limit of Piecewise function
» A function f(x) at x=a is
 → not continuous and not defined: if LHL ≠ RHL
→ not continuous and not defined: if LHL ≠ RHL
Limit of Function with abrupt change
» A function f(x) at x=a is
→ continuous: if f(a) = LHL = RHL
Limit of Functions that are not defined
» A function f(x) at x=a is
→ not defined: if LHL ≠ RHL and f(a)∉ℝ
check nature of function at a point
To decide if a function f(x) is defined at an input value x=a, the following are examined.
f(x)∣x=a
limx→a-f(x)
limx→a+f(x)
It is important to note that the L'Hospital's rule is applicable only if the limit exists. The discussion in this topic is about finding if the limit exists or not. So the L'Hospital's rule is not used in finding the limits.
When a function is examined at an input value, the possible deductions one can make about the function at that input value are
Function is continuous.
Function is not continuous but defined.
Function is not continuous and not defined.
Whether a function is continuous or defined or not defined is determined by examining
• value at the input value,
• left-hand-limit at the input value, and
• right-hand-limit at the input value.
summary
Describing a function: A function f(x) is evaluated for three values to describe at an input value x=a
•
f(a)
•
limx→a-f(x)
•
limx→a+f(x)
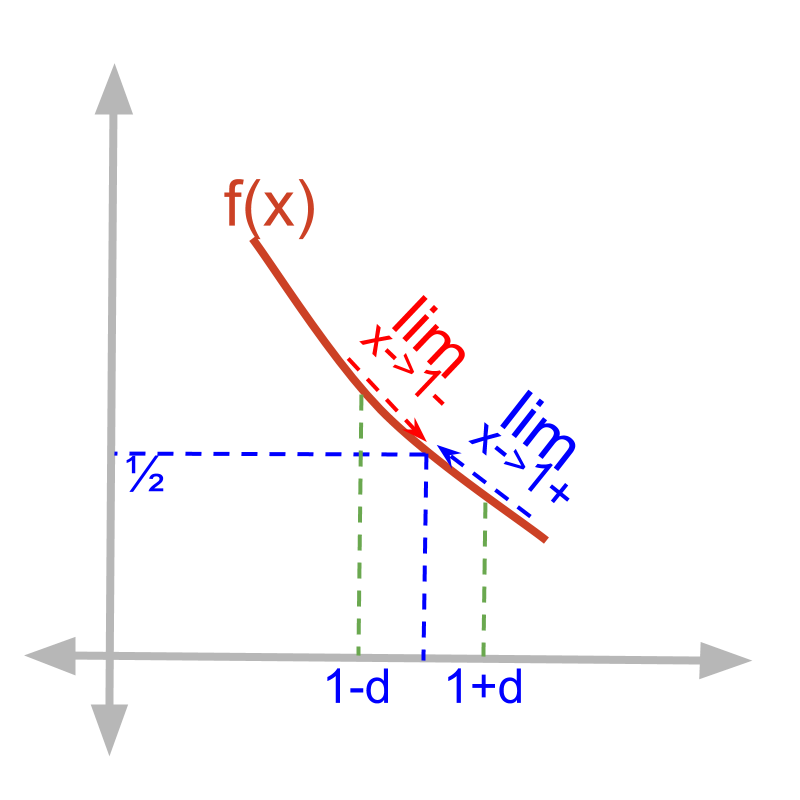
limit of continuous functions

Consider f(x)=1x2+1
f(x)∣x=1
Substitute x=1
=11+1
=12
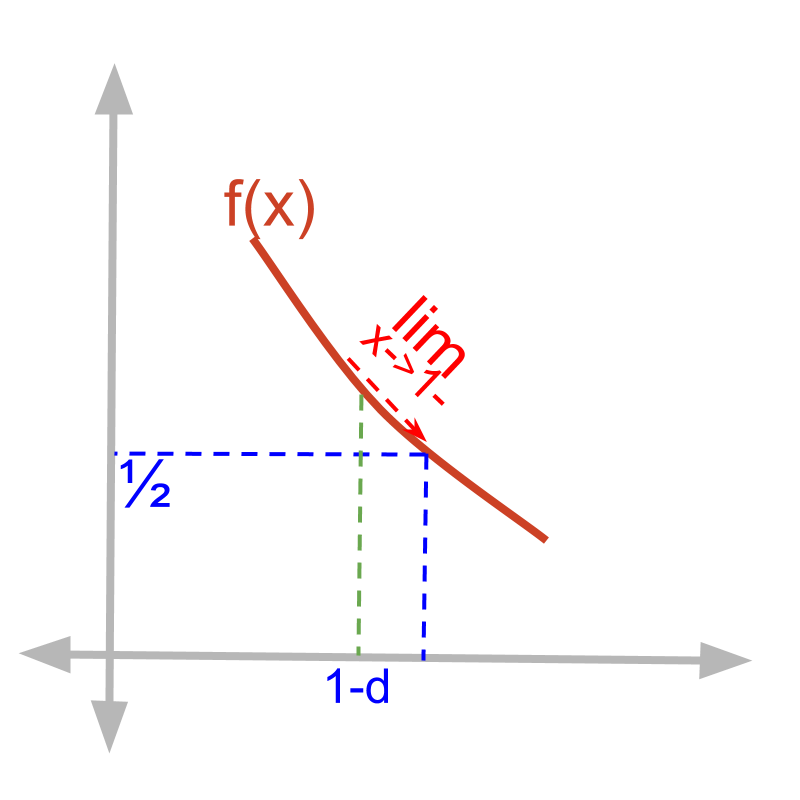
Given function f(x)=1x2+1.
The left-hand-limit limx→1-f(x)
=1(1-δ)2+1
=11-2δ+δ2+1
=12-2δ+δ2
=12 (substituting δ=0)
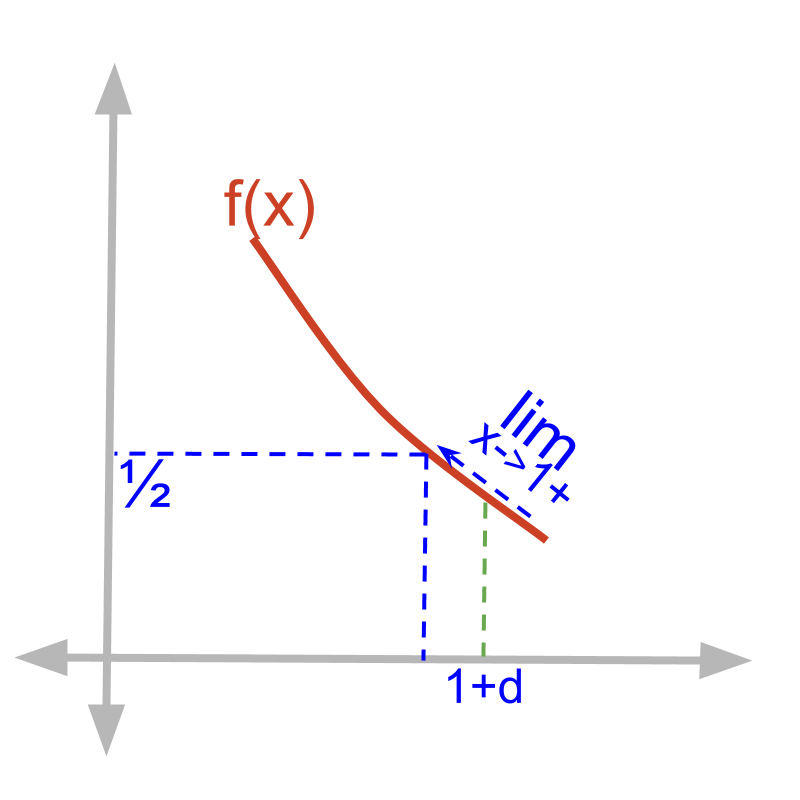
Given function f(x)=1x2+1.
The right-hand-limit limx→1+f(x)
=1(1+δ)2+1
=11+2δ+δ2+1
=12+2δ+δ2
=12 (substituting δ=0)

Given function f(x)=1x2+1.
• f(1)=12
• limx→1-f(x)=12
• limx→1+f(x)=12
The function is continuous at x=1.
Note: Though, as part of the topic, the functions that are discontinuous or indeterminate or non-differentiable are mainly handled, finding limits is not only for those kind of functions. Any function at any point can be evaluated for limits.
Function is continuous if all three values (1) function evaluated at the point, (2) left-hand-limit at the point and (3) right-hand-limit at the point are equal.
example
Given function f(x)=sinx, is it continuous at input values x=0,π2,π?
The answer is 'Continuous at all three input values'. This is a trivial problem as there is no
summary
Function is continuous: if f(a) =limx→a-f(x) =limx→a+f(x), then the function is continuous at x=a.
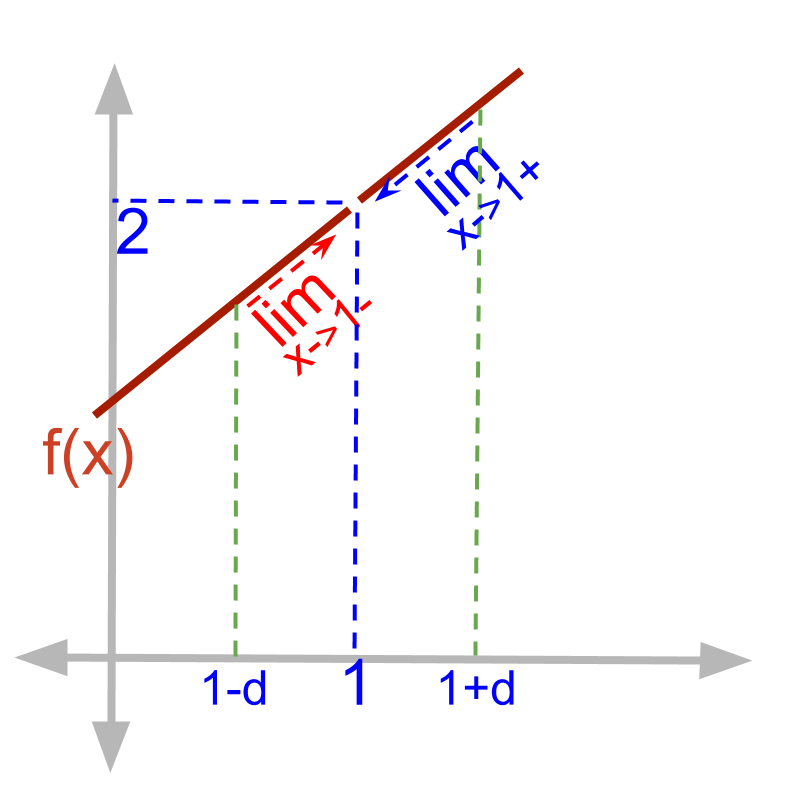
Limit of defined functions
Given function f(x)=x2-1x-1.
f(x)∣x=1
Substituting x=1
=1-11-1
=00
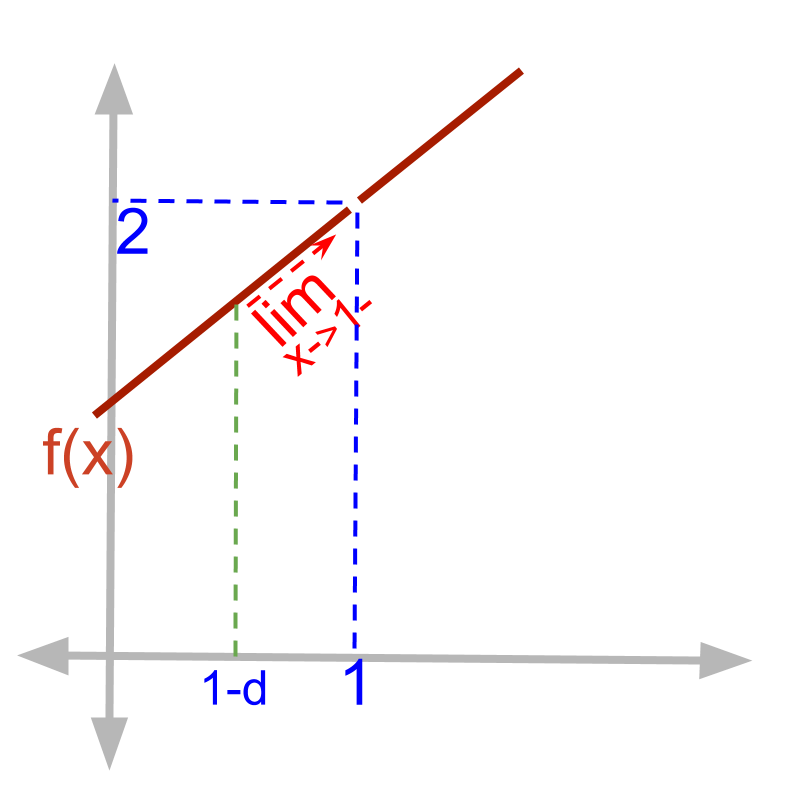
Given function f(x)=x2-1x-1.
The left-hand-limit limx→1-f(x)
=(1-δ)2-1(1-δ)-1
=1-2δ+δ2-11-δ-1
=-δ(2-δ)-δ
=2-δ
=2 (substituting δ=0)
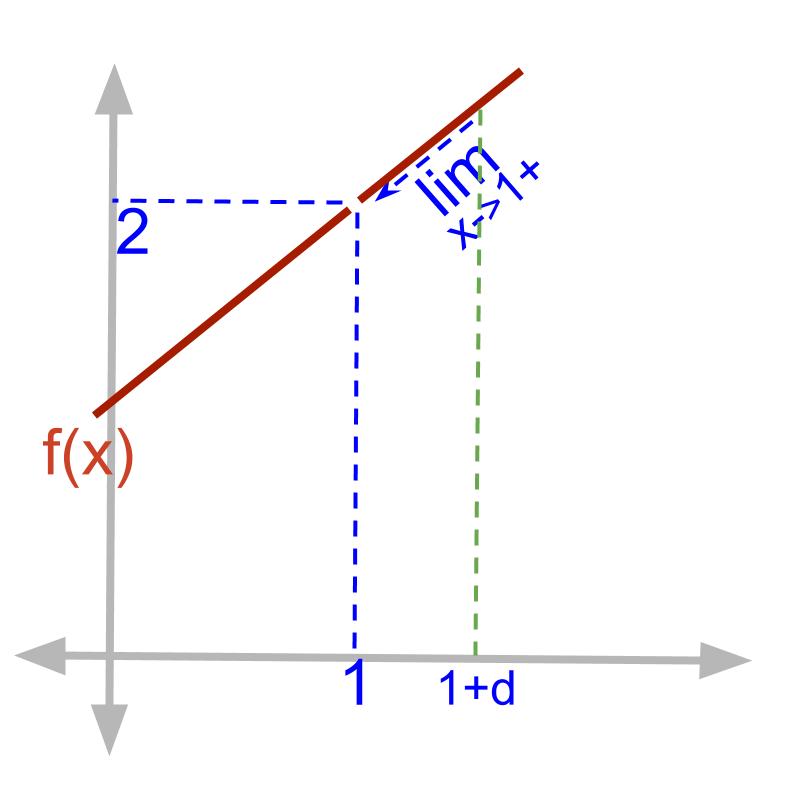
Given function f(x)=x2-1x-1.
The right-hand-limit limx→1+f(x)
=(1+δ)2-1(1+δ)-1
=1+2δ+δ2-11+δ-1
=δ(2+δ)δ
=2+δ
=2 (substituting δ=0)

Given function f(x)=x2-1x-1.
• f(1)=00 indeterminate value
• limx→1-f(x)=2
• limx→1+f(x)=2
The function is defined at x=1.
When left-hand-limit and right-hand-limit are equal, then limit is defined. The two limits together are referred as "limit of the function".
That is, when it is mentioned / referred as "limit of a function", it means, both left and right hand limits are equal.
If the left hand and right hand limits are equal then the limit is defined at that input value.
If the function evaluates to indeterminate value and the limit is defined, then the function is defined by the limits.
example
Find if the function f(x)=3x2-2x-8x-2 is continuous or defined at x=2?
The answer is 'Not Continuous and Defined'
summary
Limit is defined: If limx→a-f(x) =limx→a+f(x) then the limits are commonly given as limx→af(x)
Function is defined by Limit: If f(a)∉ℝ and limx→a-f(x) =limx→a+f(x), then the function is defined by limit at x=a.
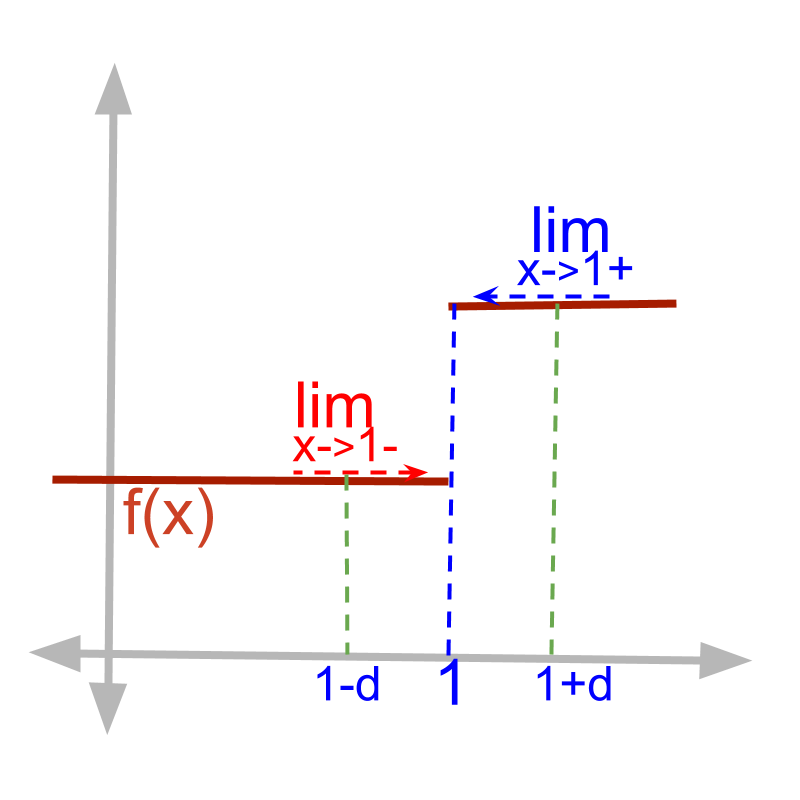
Limit of piecewise functions
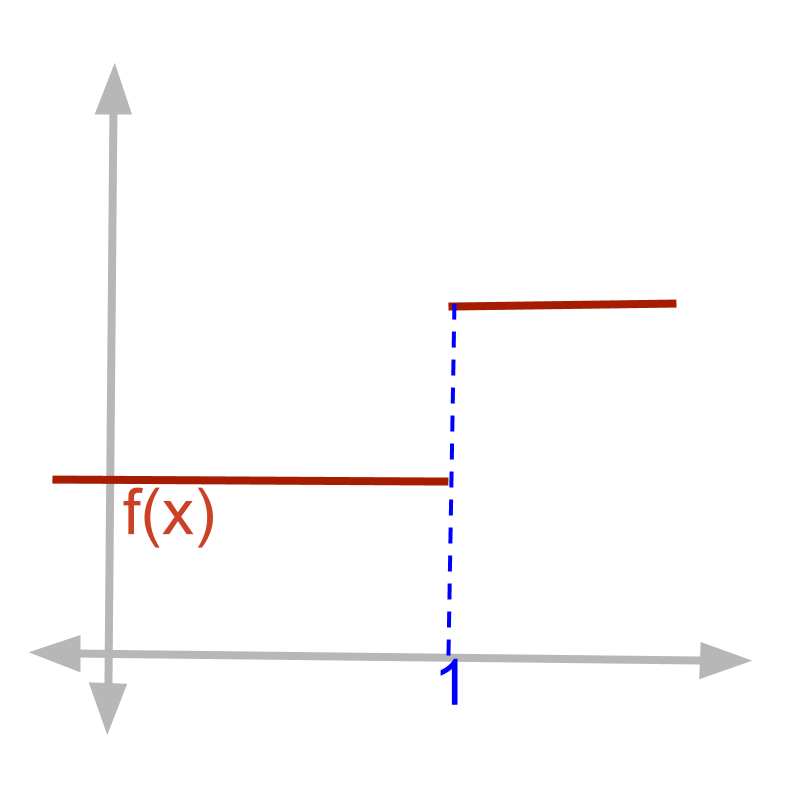
Given piecewise function
f(x)={1 for x≥10.5 for x<1
f(x)∣x=1=1 as given by definition of the function.

Given function
f(x)={1 for x≥10.5 for x<1
The left-hand-limit limx→1-f(x)
=f(x)∣x=1-δ
=0.5 (as 1-δ<1)
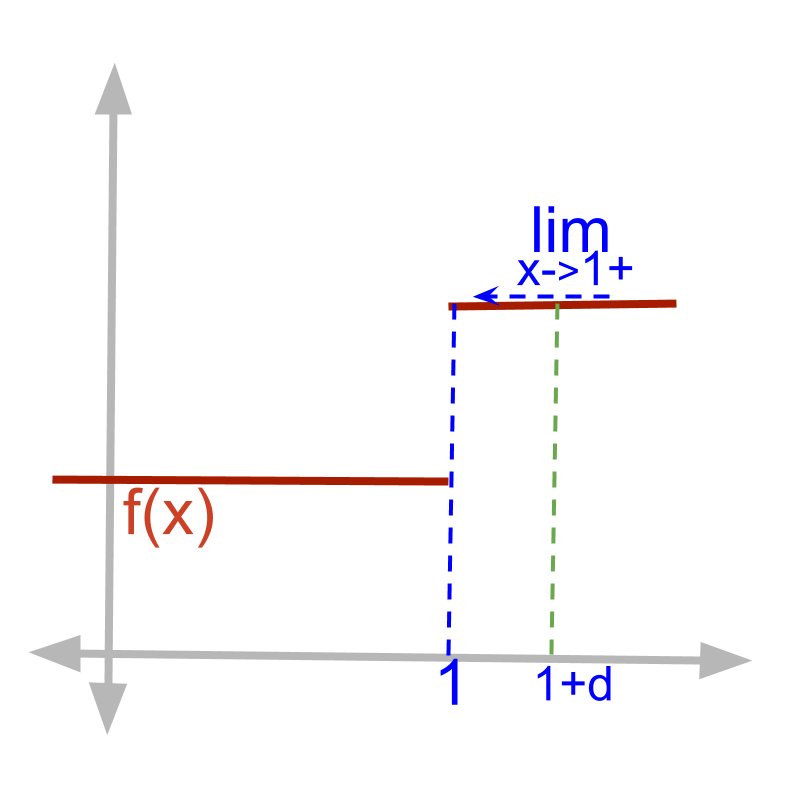
Given function
f(x)={1 for x≥10.5 for x<1
The right-hand-limit limx→1+f(x)
=f(x)∣x=1+δ
=1 (as 1+δ>1)

Given function
f(x)={1 for x≥10.5 for x<1
• f(1)=1
• limx→1-f(x)=0.5
• limx→1+f(x)=1
The function is not continuous at x=1. But, the function is defined by the given definition of the function.
If the function evaluates to a real number, then the function is defined at that input value. The limit need not be defined.
example
Given function
f(x)={2x for x>2x2 for x=2|x|+2 for x<2
Examine the function at x=2.
The answer is 'All the above'.
summary
Function is defined by value: If f(a)∈ℝ, and limx→a-f(x) ≠limx→a+f(x), then function is not continuous but defined by the definition of the function.
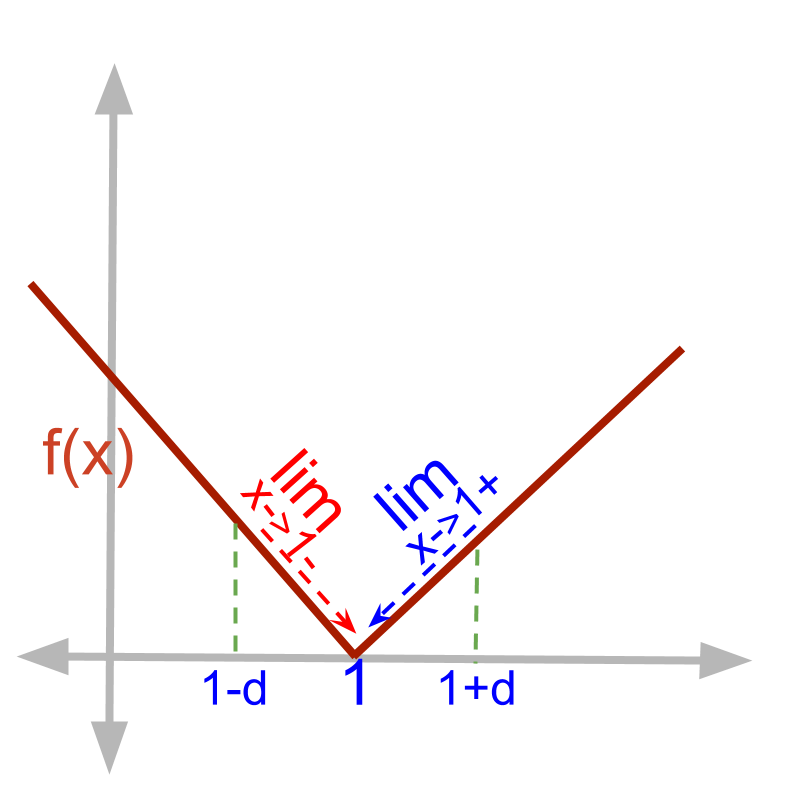
Limit of functions with abrupt change
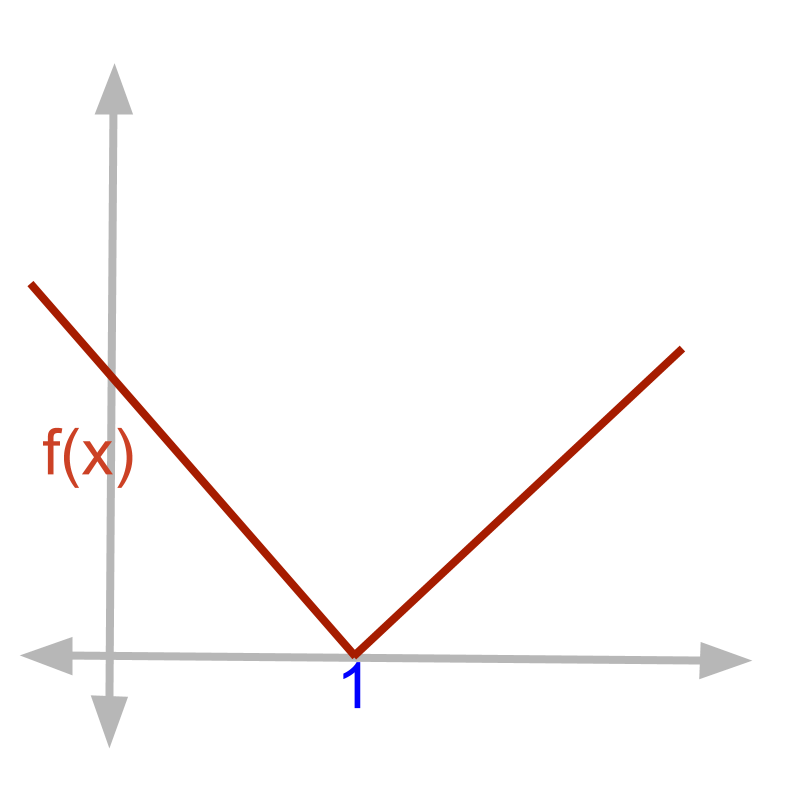
Given function f(x)=|x-1|.
f(x)∣x=1
=|1-1|
=0
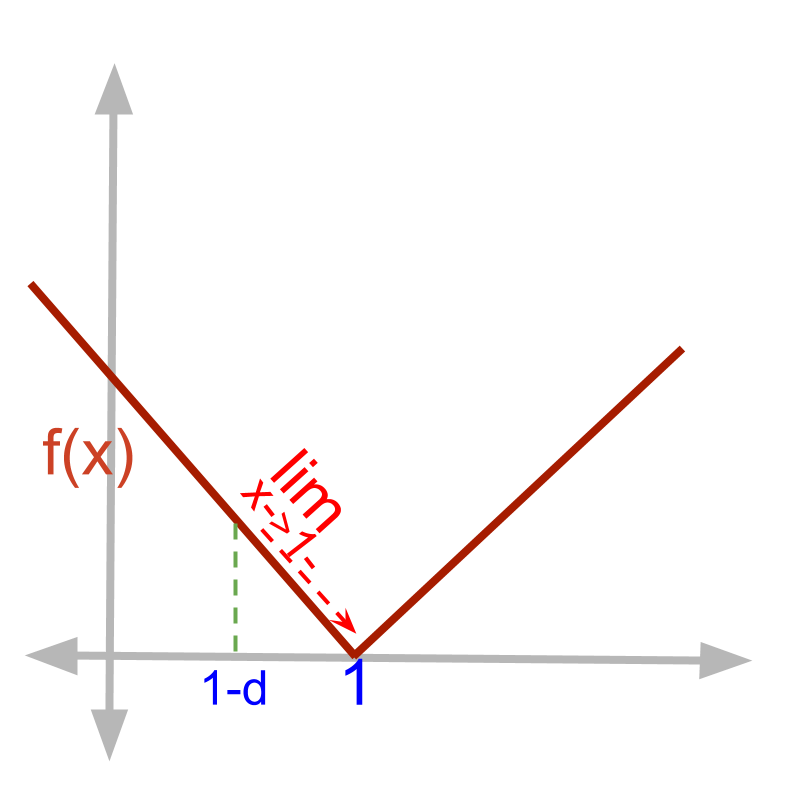
Given function f(x)=|x-1|.
The left-hand-limit limx→1-f(x)
=|1-δ-1|
=|-δ|
=δ
=0 substituting δ=0

Given function f(x)=|x-1|.
The right-hand-limit limx→1+f(x)
=|1+δ-1|
=|δ|
=δ
=0 substituting δ=0

Given function f(x)=|x-1|.
• f(1)=0
• lim_(x->1-)f(x) = 0
• lim_(x->1+)f(x) = 0
The function is continuous at x=1. Note that the function undergoes an abrupt change at x=1.
• for x<1, the slope of the line is -1
• for x>1, the slope of the line is 1
• At x=1, the slope of the line is not defined.
example
Given the function f(x)=|sin x|. Is the function continuous or defined at x=pi?
The answer is 'continuous'
Limit of Functions that are not defined

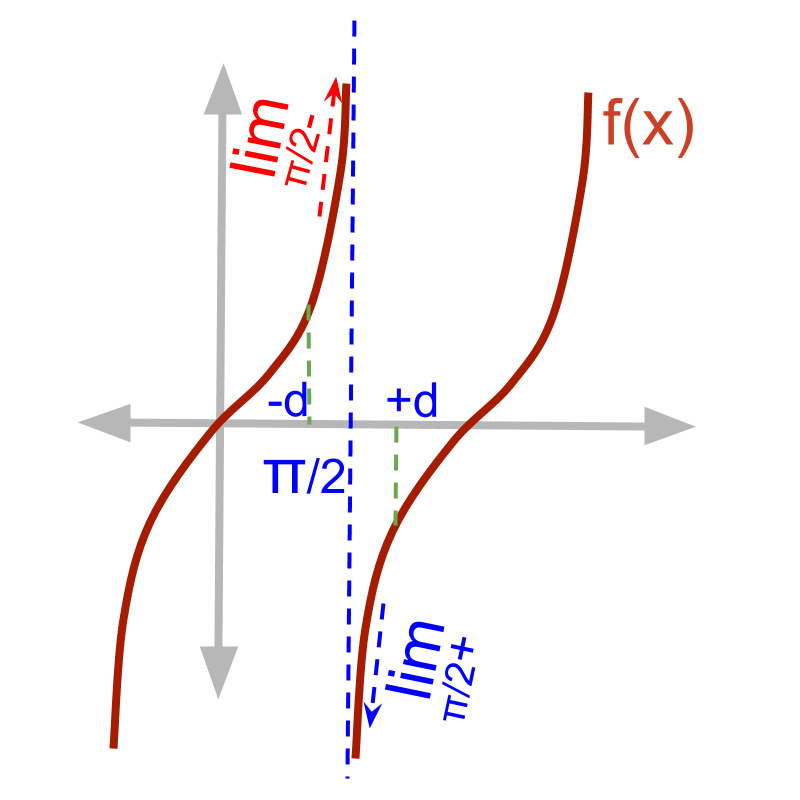
Given function f(x)=tan x.
f(x)|_(x=pi/2)
quad quad = tan(pi/2)
quad quad = oo
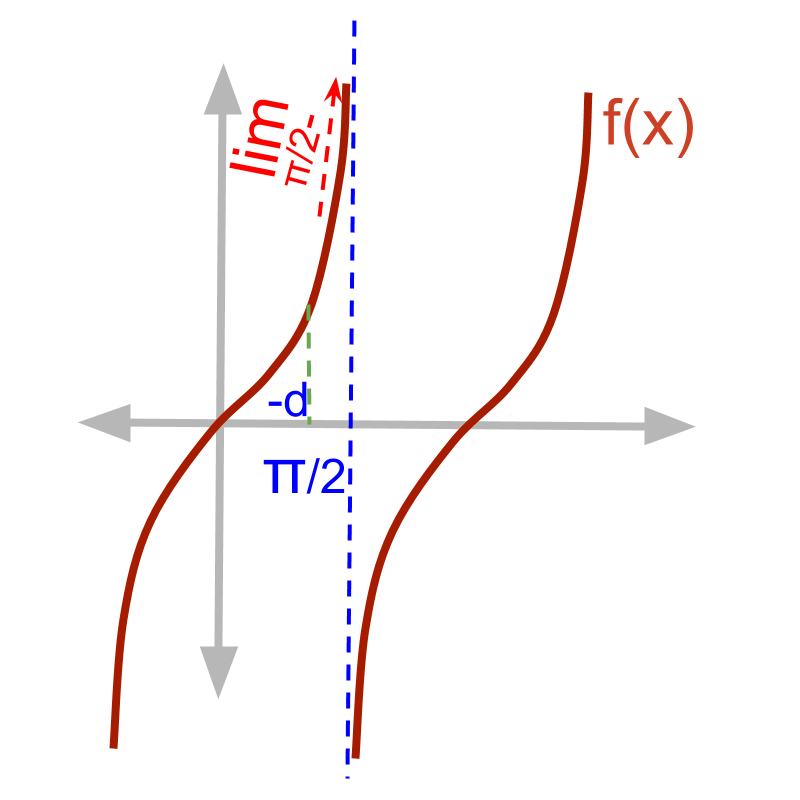
Given function f(x)=tan x.
The left-hand-limit lim_(x->pi/2-)f(x)
quad quad = f(pi/2-delta)
quad quad = tan(pi/2-delta)
quad quad = (sin(pi/2-delta))/(cos(pi/2-delta))
quad quad = (cos(delta))/(sin(delta))
quad quad = 1/0
quad quad = oo
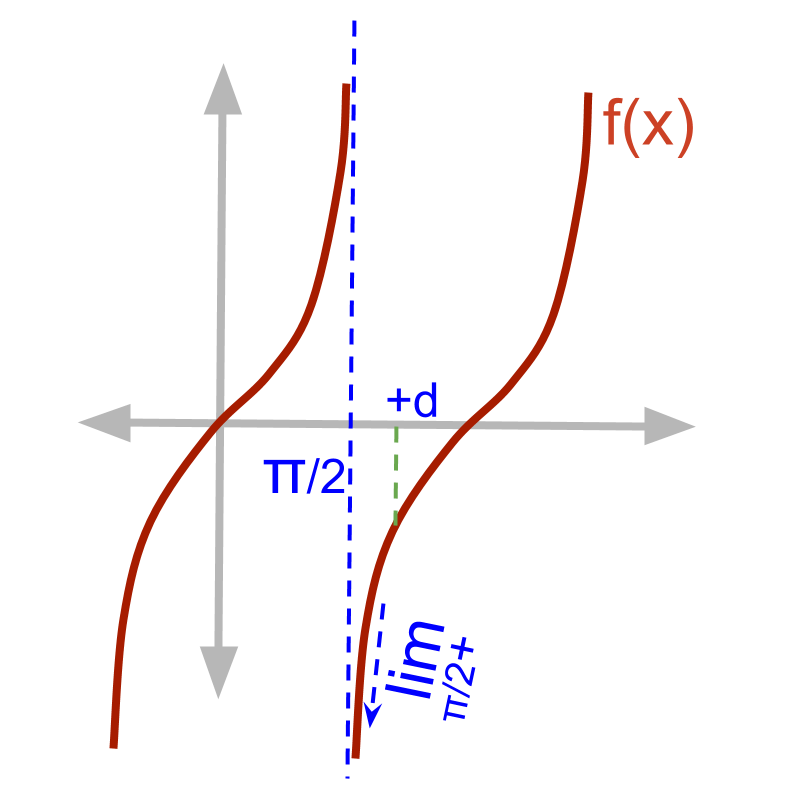
Given function f(x)=tan x.
The right-hand-limit lim_(x->pi/2+)f(x)
quad quad = f(pi/2+delta)
quad quad = tan(pi/2+delta)
quad quad = (sin(pi/2+delta))/(cos(pi/2+delta))
quad quad = (cos(delta))/(-sin(delta))
quad quad = -1/0
quad quad = -oo

Given function f(x)=tan x.
• f(pi/2)=oo
• lim_(x->pi/2-)f(x) = oo
• lim_(x->pi/2+)f(x) = -oo
The function is not continuous and not defined at x=pi/2.
If the function evaluates to +-oo or 0/0 and the limits are not equal, then the function is not defined at that input value.
If a function does not have value in real numbers and the two limits are not equal then the function is not defined at that input value.
example
Examine the function f(x) = 1/(x-3) at x=3.
The answer is 'Not defined'
summary
Function not Defined: If f(a) !in RR and lim_(x->a-)f(x) !=lim_(x->a+)f(x) then the function is not defined at x=a.
Outline
The outline of material to learn "limits (calculus)" is as follows.
Note : click here for detailed outline of Limits(Calculus).
→ Indeterminate and Undefined
→ Indeterminate value in Functions
→ Expected Value
→ Continuity
→ Definition by Limits
→ Geometrical Explanation for Limits
→ Limit with Numerator and Denominator
→ Limits of Ratios - Examples
→ L'hospital Rule
→ Examining a function
→ Algebra of Limits
→ Limit of a Polynomial
→ Limit of Ratio of Zeros
→ Limit of ratio of infinities
→ limit of Binomial
→ Limit of Non-algebraic Functions