Calculus - Limit : Understanding limits with Graphs of Numerator and Denominator

maths > calculus-limits

Understanding limits with Graphs of Numerator and Denominator

what you'll learn...

Limit of Functions with graph of numerator and denominator

» Slopes at the point $x = a$ $x=a$ decide the limits of $f (x)$ $f(x)$ at $x = a$ $x=a$ .
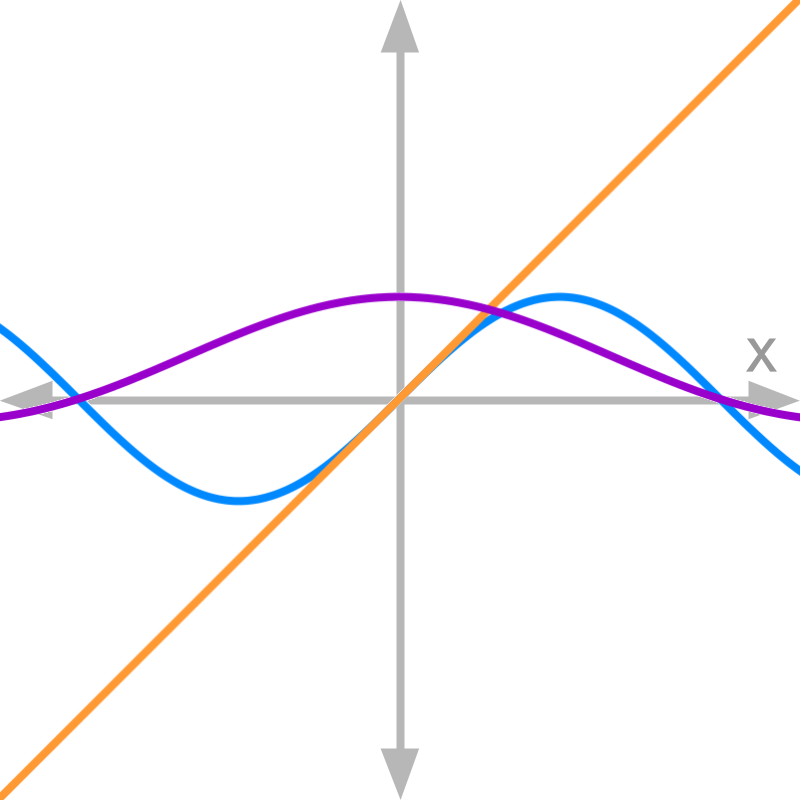limit x=a     → slope of numerator at $x = 0$ $x=0$ is $1$ $1$

    → slope of denominator at $x = 0$ $x=0$ is $1$

    → Both LHL and RHL limits $=1/1 = 1$

example

The limit of a function is computed when the function evaluates to indeterminate value $0/0$ at $x=a$ . Seeing the division in indeterminate value $0/0$ , the function can be given as $f(x)=color(deepskyblue)(f_n(x))/color(coral)(f_d(x))$ such that $color(deepskyblue)(f_n(x))|_(x=a) = 0$ and $color(coral)(f_d(x))|_(x=a) = 0$ .

Consider the function $f(x) = color(deepskyblue)(x^2-1)/color(coral)(x-1)$ . The numerator and denominator evaluate to $0$ at $x=1$ . The figure plots the numerator and denominator : numerator is the curve in blue, and denominator is the line in orange.

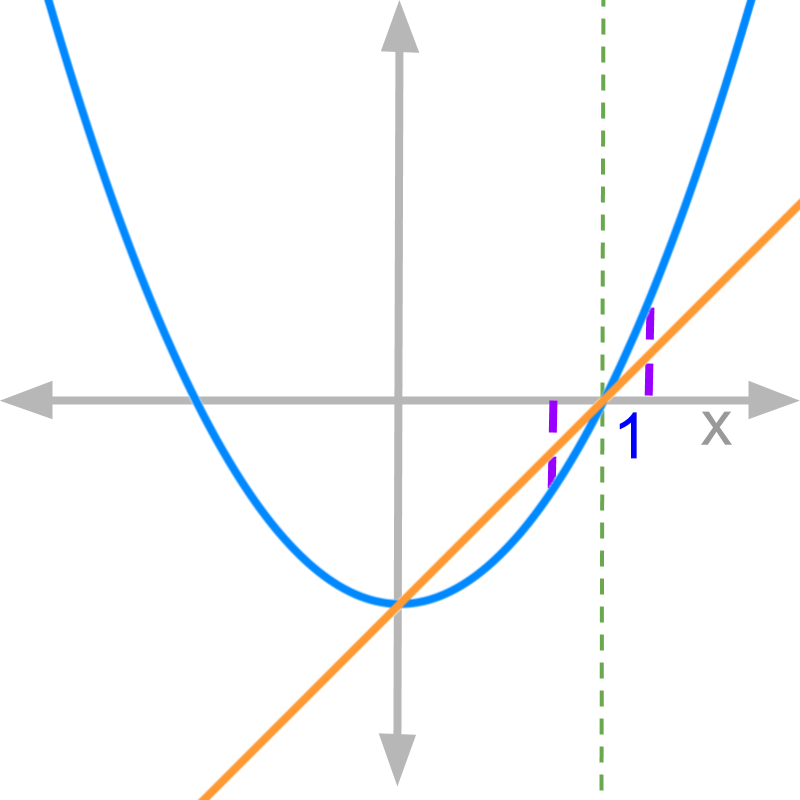
Given the graphs of numerator and denominator of the function $f(x) = color(deepskyblue)(x^2-1)/color(coral)(x-1)$ . The vertical purple lines, show $1-delta$ and $1+delta$ .

The values of denominator at $1-delta$ and $1+delta$ are $-delta$ and $+delta$ respectively.

The values of numerator at $1-delta$ and $1+delta$ are $-2delta+delta^2$ and $+2delta+delta^2$ respectively.

Given the graphs of numerator and denominator of the function $f(x) = color(deepskyblue)(x^2-1)/color(coral)(x-1)$ . The vertical purple lines, show $1-delta$ and $1+delta$ .

It is noted that the slope of the line defines the values of numerator at $1-delta$ and $1+delta$ .

formal restatement

Given the function $f(x)=color(deepskyblue)(f_n(x))/color(coral)(f_d(x))$ such that $color(deepskyblue)(f_n(x))$ $|_(x=a) = 0$ and $color(coral)(f_d(x))|_(x=a) = 0$ .

$f(x)|_(x=a+delta)$
$quad quad = color(deepskyblue)(f_n(x))|_(x=a+delta) -: color(coral)(f_d(x))|_(x=a+delta)$
$quad quad = [color(deepskyblue)(f_n(x))|_(x=a+delta) - f_n(a)]$
$quad quad quad quad -: [color(coral)(f_d(x))|_(x=a+delta) - f_d(a)]$
as $f_n(a) = 0$ and $f_d(a)=0$ .

$quad quad = [color(deepskyblue)(f_n(x))|_(x=a+delta) - f_n(a)]/delta$
$quad quad quad quad -: [color(coral)(f_d(x))|_(x=a+delta) - f_d(a)]/delta$
$quad quad = color(deepskyblue)(text(slope) f_n(x)|_(x=a)) -: color(coral)(text(slope) f_d(x)|_(x=a))$ .

summary

Geometrical representation of Limits: If $f(x)=color(deepskyblue)(f_n(x))/color(coral)(f_d(x))$ , where
$f(x)|_(x=a) = 0/0$ ;
$color(deepskyblue)(f_n(x))|_(x=a) = 0$ and
$color(coral)(f_d(x))|_(x=a) = 0$ , then

• the slopes on the left of $x=a$ define the left-hand-limit and

• the slopes on the right of $x=a$ define the right-hand-limit.

The slopes referred are for the numerator and denominator.

Outline

The outline of material to learn "limits (calculus)" is as follows.

Note : click here for detailed outline of Limits(Calculus).

→ Indeterminate and Undefined

→ Indeterminate value in Functions

→ Expected Value

→ Continuity

→ Definition by Limits

→ Geometrical Explanation for Limits

→ Limit with Numerator and Denominator

→ Limits of Ratios - Examples

→ L'hospital Rule

→ Examining a function

→ Algebra of Limits

→ Limit of a Polynomial

→ Limit of Ratio of Zeros

→ Limit of ratio of infinities

→ limit of Binomial

→ Limit of Non-algebraic Functions