Calculus - Limit : Limit of Trigonometric / Logarithmic / Exponential Functions

maths > calculus-limits

Limit of Trigonometric / Logarithmic / Exponential Functions

what you'll learn...

Limit of Trigonometric Functions

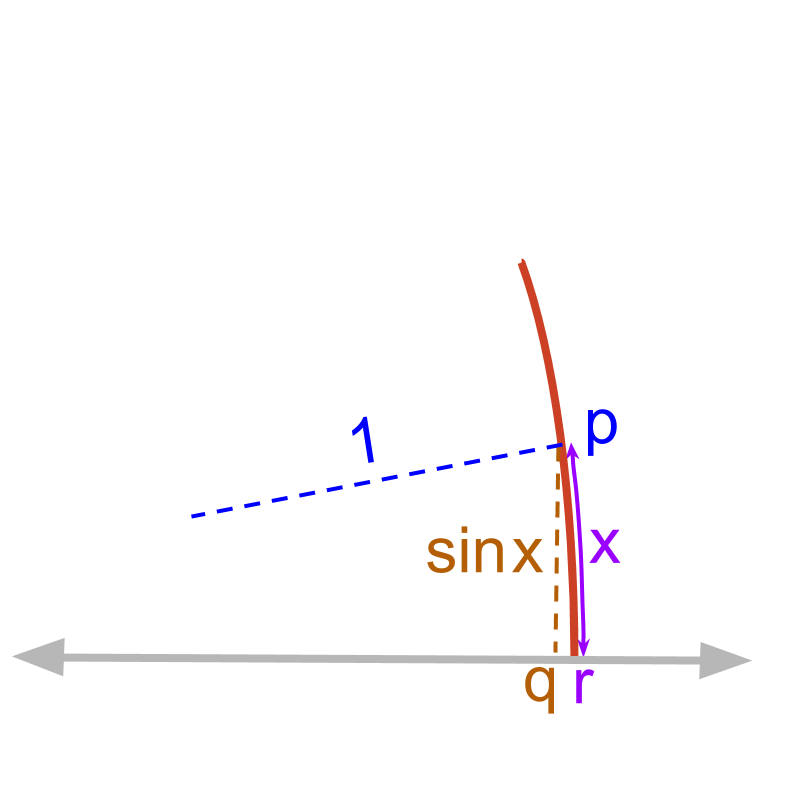chord length equals arc length for tiny angles

» $lim x \to 0 \frac{sin x}{x} = 1$ $lim_(x->0) (sin x )/x = 1$

» $lim x \to 0 \frac{arcsin x}{x} = 1$ $lim_(x->0) (arcsin x )/x = 1$

chord distance equals 0 compared to arch length for tiny angles

» $lim x \to 0 \frac{1 - cos x}{x} = 0$ $lim_(x->0) (1-cos x )/x = 0$

Limit of Logarithmic Functions

this part is not explained in detail owing to the limited time. If you would like this topic, feel free to drop in an email.

» $lim x \to 0 \frac{ln (1 + x)}{x} = 1$ $lim_(x->0) (ln(1+x))/x = 1$

» $lim x \to 0 \frac{a^{x} - 1}{x} = ln (a)$ $lim_(x->0) (a^x-1)/x = ln(a)$

Limit of Exponential Functions

this part is not explained in detail owing to the limited time. If you would like this topic, feel free to drop in an email.

» $lim x \to \infty {(1 + \frac{a}{x})}^{x} = e^{a}$ $lim_(x->oo) (1+a/x)^x = e^a$

» $lim_(x->0) (e^x -1)/x = 1$

» $lim_(x->oo) a^x$ $= {:(oo if a> 1),$ and $(0 if a<1)$

» $lim_(x->0) ((1+x)^n - 1)/x = n$

» $lim_(x->0) (sin^(-1)x) /x = 1$

problem

How to find the expected value for $f(x) = (sin x)/x$ at $x=0$ ?

When a function evaluates to $0/0$ at an input value, the common factors of the numerator and denominators are canceled to calculate the limit of the function at the input value. That works only if the numerator and denominator are polynomials.

When one of the numerator or denominator is a trigonometric function, how to compute the limits?

multiple solutions

There are multiple proofs for $lim_(x->0) (sin x)/x = 1$ .

• Substitute series expansion
$sin x = x - x^3/(3!) + x^5/(5!) + cdots$

• Geometrically prove that
$cos x <(sin x)/x < 1$

• Use the L'hospital's rule to differentiate numerator and denominator

In this, an intuitive understanding (not a proof) is given.

to understand

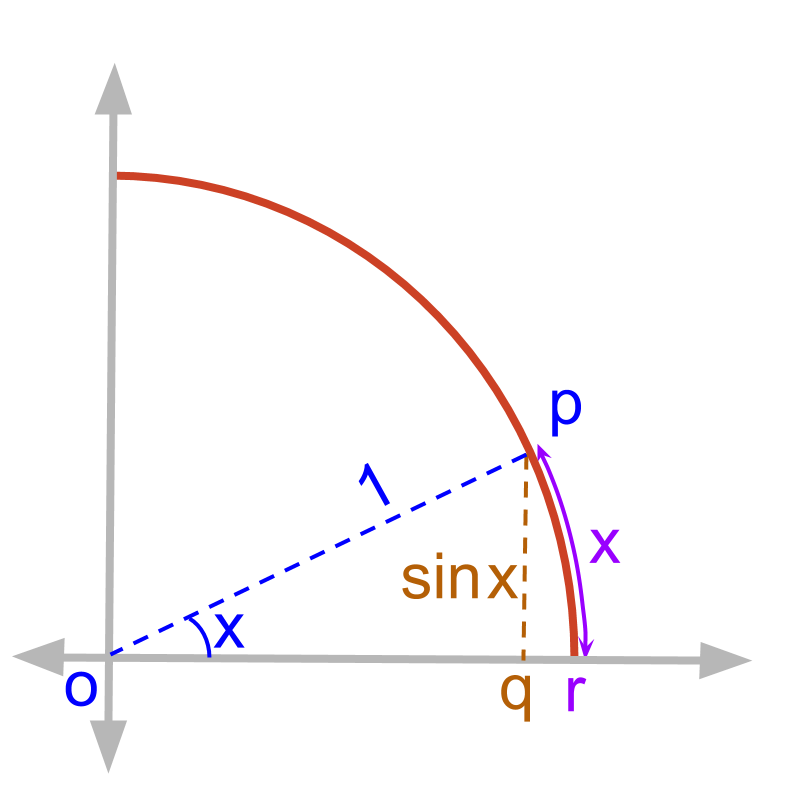
intuitive understanding of sin x / x limit

Consider the unit circle with angle $x$ radians.

Length of line segment $qp = sin x$
length of arc $rp$ = $x$

The ratio $(sin x)/x = (text(length)(qp)) /(text(length)(rp))$

intuitive understanding of sin x / x limit x tending to 0

As $x->0$ , the figure is zoomed in to the part $qp$ and $rp$ .

As $x$ is getting closer to $0$ , the length of arc $rp$ equals the length of line $qp$ .

For very small values of $x$
$sin x = x$

Limit of sin(x)/x:
$lim_(x->0) (sin x)/x = 1$

problem and solutions

There are multiple proofs for $lim_(x->0) (1-cos x)/x = 0$ .

• Substitute series expansion
$cos x = 1-x^2/(2!) + x^4/(4!) + cdots$

• Use the equality
$1-cos x = 2 sin^2 (x/2)$
and use the previous result for $(sin x)/x$

• Use the L'hospital's rule to differentiate numerator and denominator

In this, an intuitive understanding (not proof) is given.

to understand

intuitive understanding of 1- cos x / x limit

Consider the unit circle with angle $x$ radians. The length of line segment $qr$ = $1 - cos x$
length of arc $rp$ = $x$

The ratio $(1-cos x)/x =(text(length)(qr)) /(text(length)(rp))$

intuitive understanding of 1- cos x / x limit x tending to 0

As $x->0$ , the figure is zoomed in to the part $qr$ and $rp$ .

As $x$ is getting closer to $0$ , the length of $qr$ becomes $0$ faster than the length of arc $rp$

For very small values of $x$ , $x$ is far greater than $1-cos x$ .
$x > (1-cos x) ~= 0$

Limit of (1-cos(x))/x:
$lim_(x->0) (1 - cos x)/x = 0$

example

What is $lim_(x->0) (tan x)/x$ ?

The answer is ' $1$ '
$lim_(x->0) (tan x)/x$
$quad quad = lim_(x->0) (sin x)/x xx 1/cos x$
$quad quad = 1 xx 1$

some results

Limit of Logarithmic Functions:
$lim_(x->0) (ln (1+x))/x = 1$
$lim_(x->0) (a^x-1)/x = ln a$

summary

Limit of Exponential Functions:
$lim_(x->oo) (1+a/x)^x = e^a$

$lim_(x->0) (e^x -1)/x = 1$

$lim_(x->oo) a^x = {:(oo if a> 1), and (0 if a<1)$

$lim_(x->0) ((1+x)^n - 1)/x = n$

$lim_(x->0) (sin^(-1)x) /x = 1$

Outline

The outline of material to learn "limits (calculus)" is as follows.

Note : click here for detailed outline of Limits(Calculus).

→ Indeterminate and Undefined

→ Indeterminate value in Functions

→ Expected Value

→ Continuity

→ Definition by Limits

→ Geometrical Explanation for Limits

→ Limit with Numerator and Denominator

→ Limits of Ratios - Examples

→ L'hospital Rule

→ Examining a function

→ Algebra of Limits

→ Limit of a Polynomial

→ Limit of Ratio of Zeros

→ Limit of ratio of infinities

→ limit of Binomial

→ Limit of Non-algebraic Functions