Trigonometry (advanced) : Compound Angles: Geometrical Proof for `sin(A+B)`

maths > advanced-trigonometry

Compound Angles: Geometrical Proof for $\sin (A + B)$ $sin(A+B)$

what you'll learn...

sin(A+B)

sin a+b proof » the coordinates of points
    → $P (\cos A, \sin A)$ $P (cosA, sinA)$
    → $Q (\cos B, \sin B)$ $Q (cosB, sinB)$
    → $R (\cos (A + B), \sin (A + B))$ $R (cos(A+B), sin(A+B))$
    → $Q 1 (\sin B, \cos B)$ $Q1 (sinB, cosB)$
    → $T (0, 1)$ $T (0, 1)$

» equate the distance $\bar{R T} = \bar{P Q 1}$ $bar(RT) = bar(PQ1)$

» $\sin (A + B)$ $sin(A+B)$ $= \sin A \cos B$ $=sinAcosB$ $+ \cos A \sin B$ $+ cosAsinB$

cos(A+B)

cos a+b proof » equate the distance $\bar{R S} = \bar{P Q 2}$ $bar(RS) = bar(PQ2)$

» $\cos (A + B)$ $cos(A+B)$ $= \cos A \cos B$ $=cosAcosB$ $- \sin A \sin B$ $- sinAsinB$

problem definition

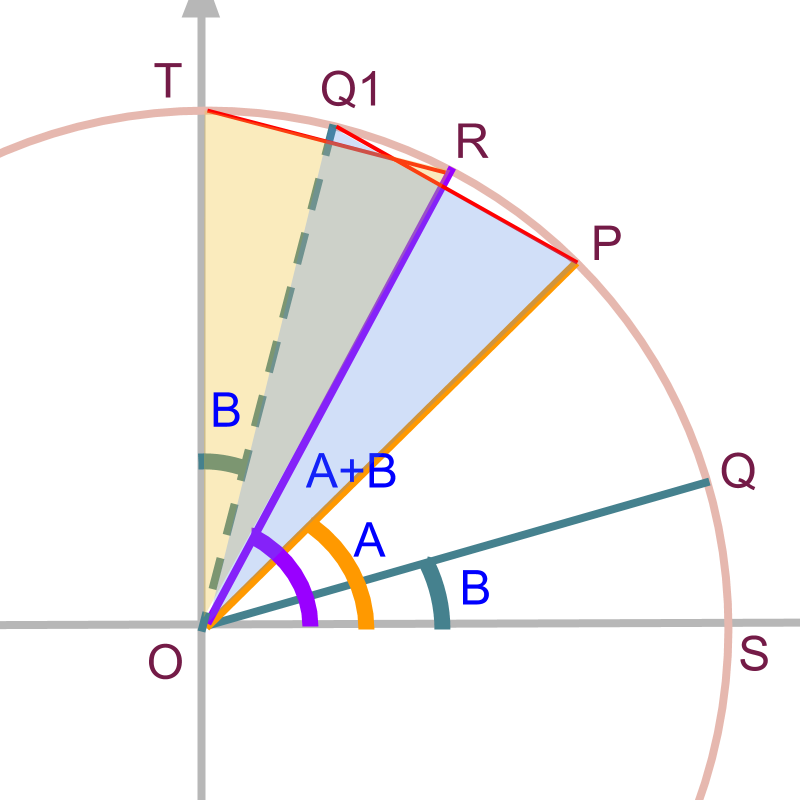
Consider points $P$ $P$ and $Q$ $Q$ with angles $∠ A$ $/_A$ and $∠ B$ $/_B$ in unit circle as shown in the figure.

The point $P$ $P$ is $(\cos A, \sin A)$ $(cosA, sinA)$

The point Q is $(\cos B, \sin B)$ $(cosB, sinB)$

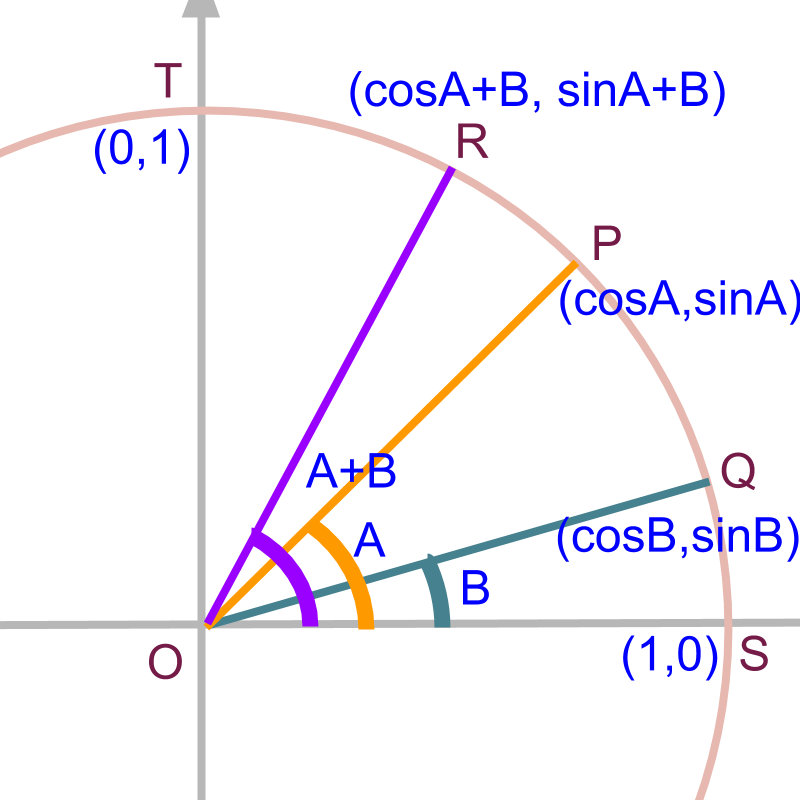
In the given figure, point $R$ $R$ is for angle $∠ (A + B)$ $/_(A+B)$ .

The point R is $(\cos (A + B), \sin (A + B))$ $(cos (A+B), sin(A+B))$ .

In the given figure, coordinates of $P$ $P$ , and $Q$ $Q$ are given. Can coordinate of $R$ $R$ be calculated?

In other words, given the trigonometric ratios of A and B , can we compute trigonometric ratios of $A + B$ $A+B$ ?
$\sin (A + B) = ?$ $sin(A+B) = ?$
$\cos (A + B) = ?$ $cos(A+B) = ?$

proof

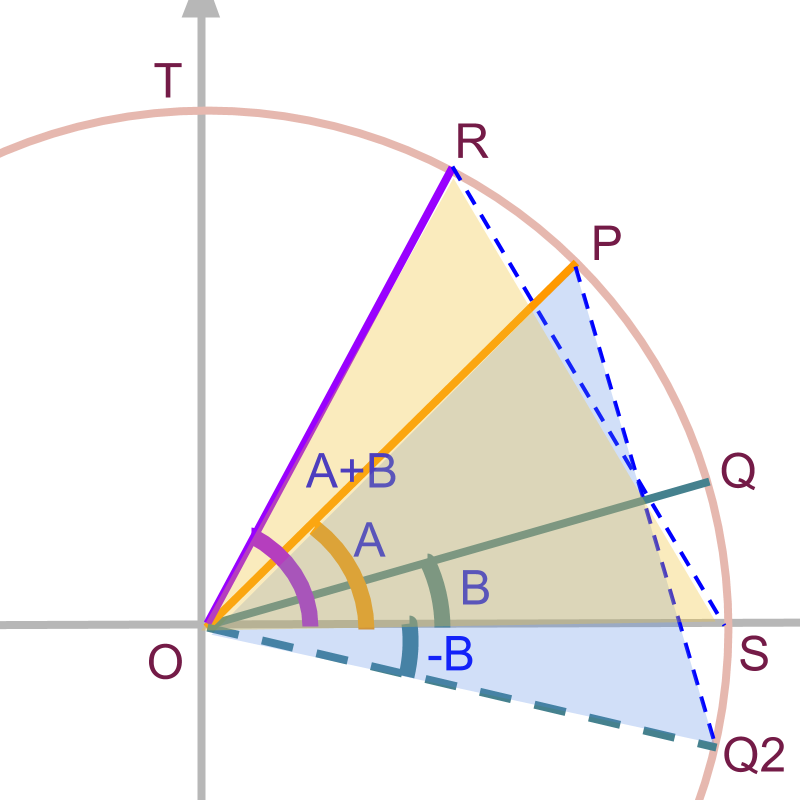
In the modified figure, point $Q 1$ $Q1$ is for angle $∠ (90 - B)$ $/_(90-B)$ .

The point $Q 1$ $Q1$ is $(\cos (90 - B), \sin (90 - B))$ $(cos (90-B), sin(90-B))$ $= (\sin B, \cos B)$ $=(sin B, cos B)$ As $\cos (90 - B) = \sin B$ $cos(90-B) = sinB$ and $\sin (90 - B) = \cos B$ $sin(90-B) = cosB$ .

In the given figure, consider point $T (0, 1)$ $T (0,1)$ .

the angle $∠ R O T$ $/_ROT$

$= ∠ S O T - ∠ S O R$ $quad quad = /_SOT -/_SOR$

$= 90 - (A + B)$ $quad quad = 90 - (A+B)$

In the given figure,

$∠ P O Q 1$ $/_POQ1$
$= ∠ S O T - ∠ S O P - ∠ Q 1 O T$ $quad quad = /_SOT -/_SOP-/_Q1OT$
$= 90 - A - B$ $quad quad = 90 - A - B$

In the given figure:
$∠ R O T = 90 - (A + B)$ $/_ROT = 90-(A+B)$
$∠ P O Q 1 = 90 - A - B$ $/_POQ1= 90-A-B$ .

That is, the angle subtended by the two chords $\bar{R T}$ $bar(RT)$ and $\bar{P Q 1}$ $bar(PQ1)$ are equal.

In the given figure, the coordinate of $R$ $R$ is $(\cos (A + B), \sin (A + B))$ $(cos(A+B), sin(A+B))$ and the coordinate of $T$ $T$ is $(0, 1)$ $(0,1)$ . So, the Square of length of chord, using the distance formula, is

${\bar{R T}}^{2}$ $bar(RT)^2$

$= {(\cos (A + B) - 0)}^{2} + {(\sin (A + B) - 1)}^{2}$ $quad quad = (cos(A+B)-0)^2 + (sin(A+B)-1)^2$

$= 2 - 2 \sin (A + B)$ $quad quad= 2-2sin(A+B)$

Square of length of chord $\bar{R T}$ $bar(RT)$ is calculated as follows.

$T (0, 1)$ $T(0,1)$
$R (\cos (A + B), \sin (A + B))$ $R(cos(A+B), sin(A+B))$

${\bar{R T}}^{2}$ $bar(RT)^2$
$= {(\cos (A + B) - 0)}^{2}$ $quad quad = color(coral)((cos(A+B)-0)^2)$
$+ {(\sin (A + B) - 1)}^{2}$ $quad quad quad + color(deepskyblue)((sin(A+B)-1)^2)$
$= \cos^{2} (A + B) + \sin^{2} (A + B)$ $quad quad = color(coral)(cos^2(A+B)) + color(deepskyblue)(sin^2(A+B))$
$+ 1 - 2 \sin (A + B)$ $quad quad quad + color(deepskyblue)(1-2sin(A+B))$
$= 2 - 2 \sin (A + B)$ $quad quad= 2-2sin(A+B)$

In the given figure, the coordinate of $P$ $P$ is $(\cos A, \sin A)$ $(cosA, sinA)$ . and the coordinate of $Q 1$ $Q1$ is $(\sin B, \cos B)$ $(sinB,cosB)$ .

The square of length of chord is

${\bar{P Q 1}}^{2}$ $bar(PQ1)^2$

$= {(\cos A - \sin B)}^{2} + {(\sin A - \cos B)}^{2}$ $quad quad = (cosA-sinB)^2 + (sinA-cosB)^2$

$= 2 - 2 \cos A \sin B - 2 \sin A \cos B$ $quad quad = 2-2cosAsinB-2sinAcosB$

Square of length of chord $\bar{P Q 1}$ $bar(PQ1)$ is calculated as follows.

$P (\cos A, \sin A)$ $P(cosA,sinA)$
$Q 1 (\sin B, \cos B)$ $Q1(sinB, cosB)$

${\bar{P Q 1}}^{2}$ $bar(PQ1)^2$
$= {(\cos A - \sin B)}^{2}$ $quad quad = color(coral)((cosA-sinB)^2$
$+ {(\sin A - \cos B)}^{2}$ $quad quad quad + color(deepskyblue)((sinA-cosB)^2)$
$= \cos^{2} (A) + \sin^{2} (A)$ $quad quad = color(coral)(cos^2(A)) + color(deepskyblue)(sin^2(A))$
$+ \sin^{2} (B) + \cos^{2} (B)$ $quad quad quad +color(coral)(sin^2(B)) + color(deepskyblue)(cos^2(B))$
$- 2 \cos A \sin B - 2 \sin A \cos B$ $quad quad quad color(coral)(-2 cosA sinB) color(deepskyblue)(-2sinA cosB)$
$= 2 - 2 \cos A \sin B - 2 \sin A \cos B$ $quad quad= 2-color(coral)(2cosAsinB)-color(deepskyblue)(2sinAcosB)$

Equating the square of lengths of chords $\bar{R T}$ $bar(RT)$ and $\bar{P Q 1}$ $bar(PQ1)$ .
$2 - 2 \sin (A + B) =$ $2-2sin(A+B)=$ $2 - 2 \cos A \sin B$ $2-2cosAsinB$ $- 2 \sin A \cos B$ $-2sinAcosB$

This proves $\sin (A + B) = \sin A \cos B + \cos A \sin B$ $sin(A+B) = sinAcosB + cosAsinB$

proof for cosine

To compute the value of $\cos (A + B)$ $cos(A+B)$ the enclosed figure is used and the proof is outlined below.

$P (\cos A, \sin A)$ $P (cosA, sinA)$
$Q (\cos B, \sin B)$ $Q (cosB, sinB)$
$R (\cos (A + B), \sin (A + B))$ $R (cos(A+B), sin(A+B))$
$S (1, 0)$ $S (1,0)$
$Q 2 (\cos B, - \sin B)$ $Q2 (cosB, -sinB)$

${\bar{P Q 2}}^{2}$ $bar(PQ2)^2$
$= {(\cos A - \cos B)}^{2}$ $quad quad = (cosA-cosB)^2$ $+ {(\sin A + \sin B)}^{2}$ $+ (sinA+sinB)^2$
$= 2 - 2 \cos A \cos B + 2 \sin A \sin B$ $quad quad = 2 -2cosAcosB+2sinAsinB$

${\bar{R S}}^{2}$ $bar(RS)^2$
$=$ $quad quad =$ ${(\cos (A + B) - 1)}^{2}$ $(cos(A+B)-1)^2$ $+ {(\sin (A + B) - 0)}^{2}$ $+ (sin(A+B)-0)^2$
$= 2 - 2 \cos (A + B)$ $quad quad = 2-2cos(A+B)$

equating these two $\cos (A + B) = \cos A \cos B - \sin A \sin B$ $cos(A+B) = cosAcosB - sinAsinB$

summary

$\sin (A + B) = \sin A \cos B + \cos A \sin B$ $sin(A+B)=sinA cosB + cosA sinB$
$\cos (A + B) = \cos A \cos B - \sin A \sin B$ $cos(A+B)=cosA cosB - sinA sinB$

Outline

It is advised to do the firmfunda version of "basics of Trigonometry" course before doing this.

The outline of material to learn "Advanced Trigonometry" is as follows.
Note: go to detailed outline of Advanced Trigonometry

→ Unit Circle form of Trigonmetric Values

→ Trigonometric Values in all Quadrants

→ Trigonometric Values or any Angles : First Principles

→ Understanding Trigonometric Values in First Quadrant

→ Trigonometric Values in First Quadrant

→ Trigonometric Values of Compound Angles: Geometrical Proof

→ Trigonometric Values of Compound Angles: Algebraic Proof

→ Trigonometric Values of Compound Angles: tan cot

→ Trigonometric Values of Compound Angles: more results