Trigonometry (advanced) : Trigonometric Values: Unit Circle Form

maths > advanced-trigonometry

Trigonometric Values: Unit Circle Form

what you'll learn...

Names of Trigonometric Functions

» Angle $θ$ $theta$ specifies a class of similar right-triangles.

    → Any one representative triangle captures the properties of all in the class.

» The representative triangle is chosen in the unit circle. triangle in unitcircle     » sine: root word meaning chord.
    » tangent: meaning touching the curve
    » secant: meaning cutting through

  » complementary: meaning completes to right angle.
    » co-sine
    » co-tangent
    » co-secant

Trigonometric Values Redefined

» Point on unit circle at the given angle

θ

$theta$
Representative of the class of similar right-triangles

» Projection on y-axis =

y

$y$
→ opposite side in triangle is generalized to the y-coordinate

» Projection on x-axis =

x

$x$
→ adjacent side in triangle is generalized to the x-coordinate

»

\sin θ = y

$sin theta = y$
y-coordinate of the point on unit circle

»

\cos θ = x

$cos theta = x$
x-coordinate of the point on unit circle

» and accordingly

\tan

$tan$ ,

\sec

$sec$ ,

\csc

$csc$ ,

\cot

$cot$ .

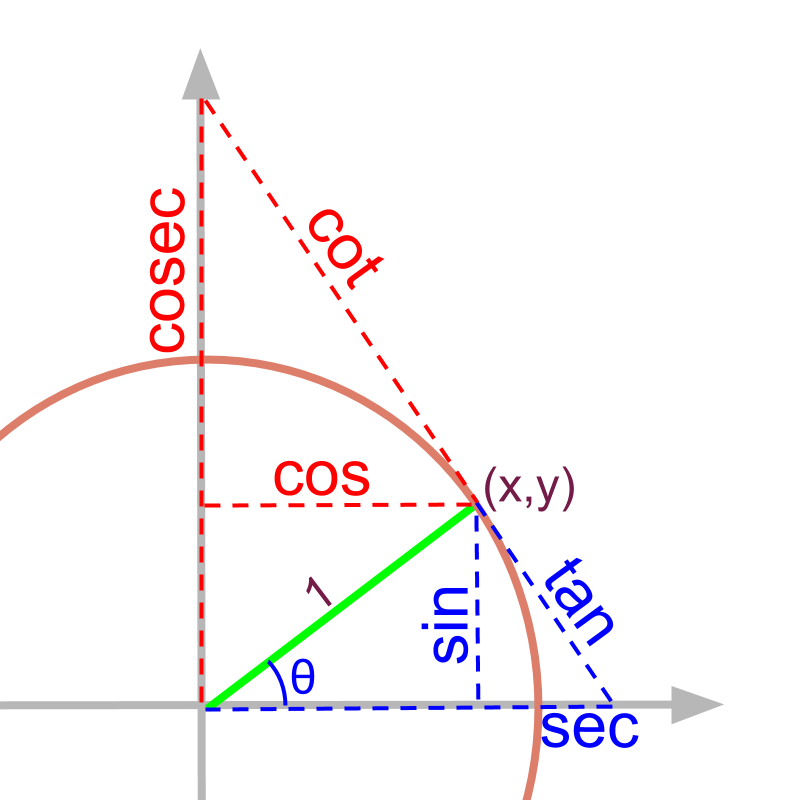
recap

When starting trigonometry, the definitions of trigonometric ratios were explained for right angled triangles.

• sine,

• cosine,

• tan (tangent),

• secant,

• co-secant, and

• cot (co-tangent)

Let us look at a refined definition of the same.

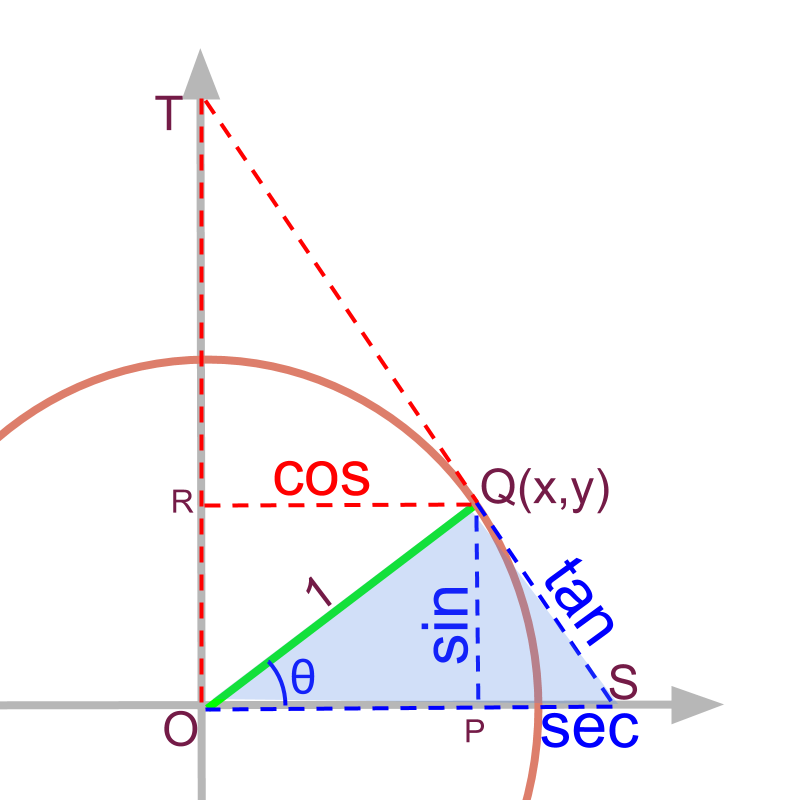
unit circle

A circle with radius $1$ $1$ unit is called an unit circle.

It was explained that trigonometric ratios are defined for set of similar right angled triangles. Consider the right angled triangle made within a unit circle as given in the figure. Any right angled triangle with one angle $θ$ $theta$ is represented by the $△ O P Q$ $/_\ OPQ$ .

The hypotenuse in the given triangle is $\bar{O Q}$ $bar(OQ)$ .

The $\bar{O P}$ $bar(OP)$ is the adjacent side and $\bar{P Q}$ $bar(PQ)$ is the opposite side to $∠ θ$ $/_theta$

chord

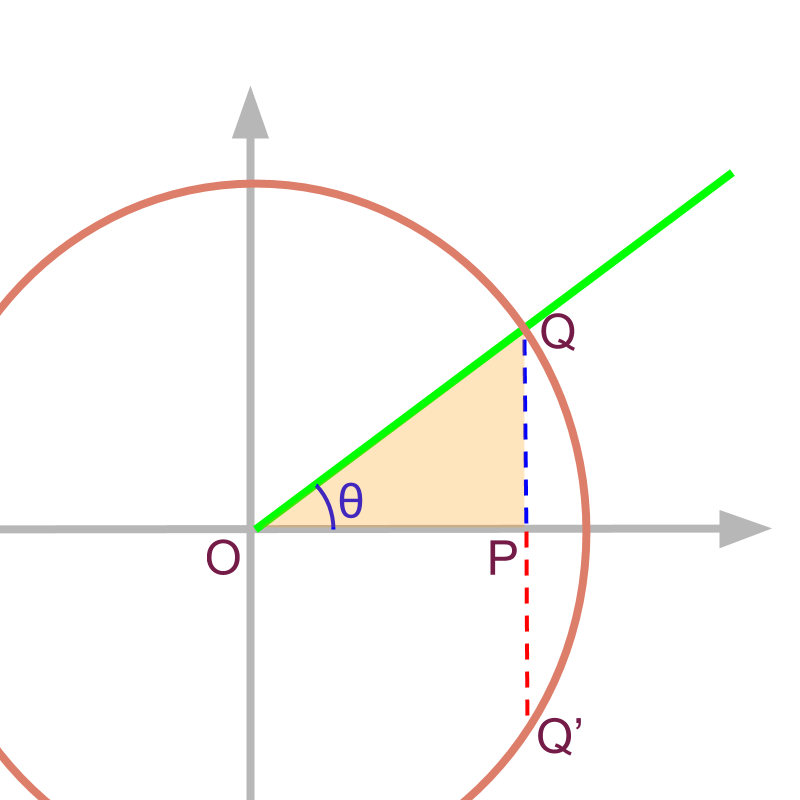
The chord to the circle is $\bar{(Q Q')}$ $bar((Q Q′)$ .

Note that in the given unit circle $\bar{O Q} = 1$ $bar(OQ)= 1$ .

$\sin θ$ $sin theta$ in the given figure is $\bar{P Q} \div \bar{O Q}$ $bar(PQ) -: bar(OQ)$ $= \bar{P Q}$ $= bar(PQ)$

The root word of $\sin$ $sin$ refers to chord of a circle.

For a given angle $θ$ $theta$ , the line $\bar{P Q}$ $bar(PQ)$ is half of the chord as shown in figure. So the ratio is named as $\sin$ $sin$ referring the relation to length of the chord at the given angle.

redefine sine

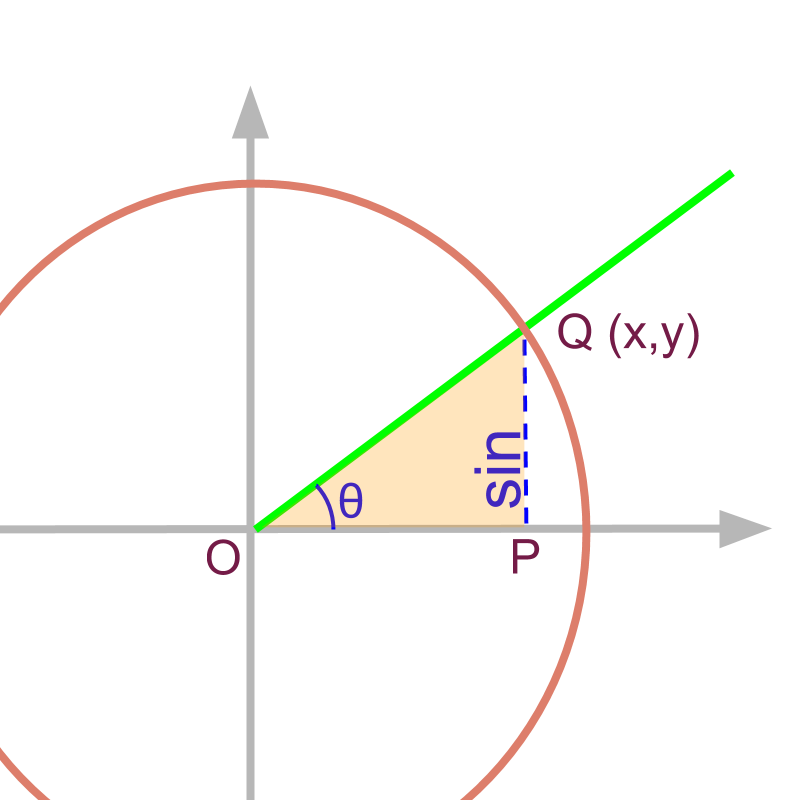
Given that the point $Q$ $Q$ is $(x, y)$ $(x,y)$ ,

$\sin θ = y$ $sin theta = y$

So far, $\sin, \cos, ...$ $sin, cos, ...$ were referred as trigonometric ratios. Considering the unit circle and the point $(x, y)$ $(x, y)$ at angle $θ$ $theta$ on the unit circle, $\sin, \cos ...$ $sin, cos ...$ are referred as trigonometric values.

$\sin θ$ $sin theta$ is the projection on y-axis for the line of unit length at angle $θ$ $theta$ .

complementary

The complementary angle of an angle $θ$ $theta$ is $90 - θ$ $90-theta$ .

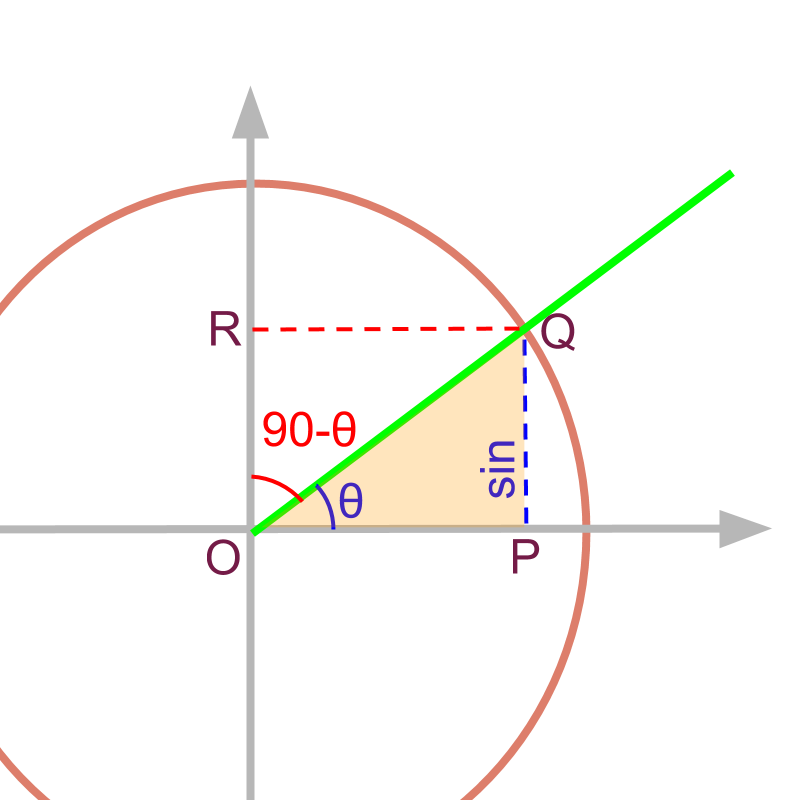
The complementary angle for $∠ P O Q = θ$ $/_POQ = theta$ is $∠ Q O R$ $/_QOR$ .

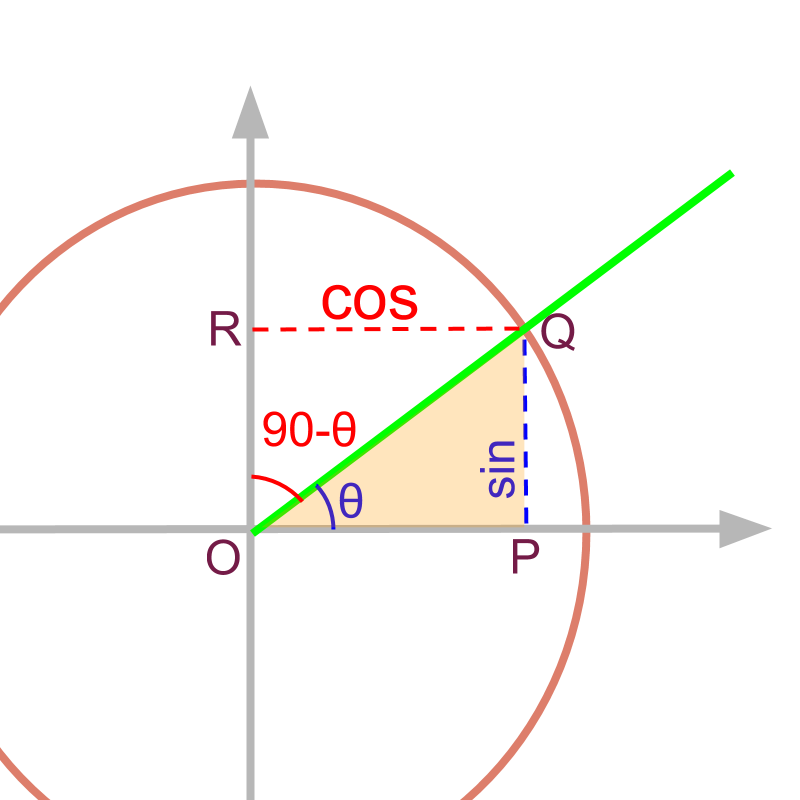
For a given angle $θ$ $theta$ , the $\sin$ $sin$ of complementary angle is $\cos$ $cos$ or cosine.

co-sine is the short form of 'complementary sine'.

redefine cosine

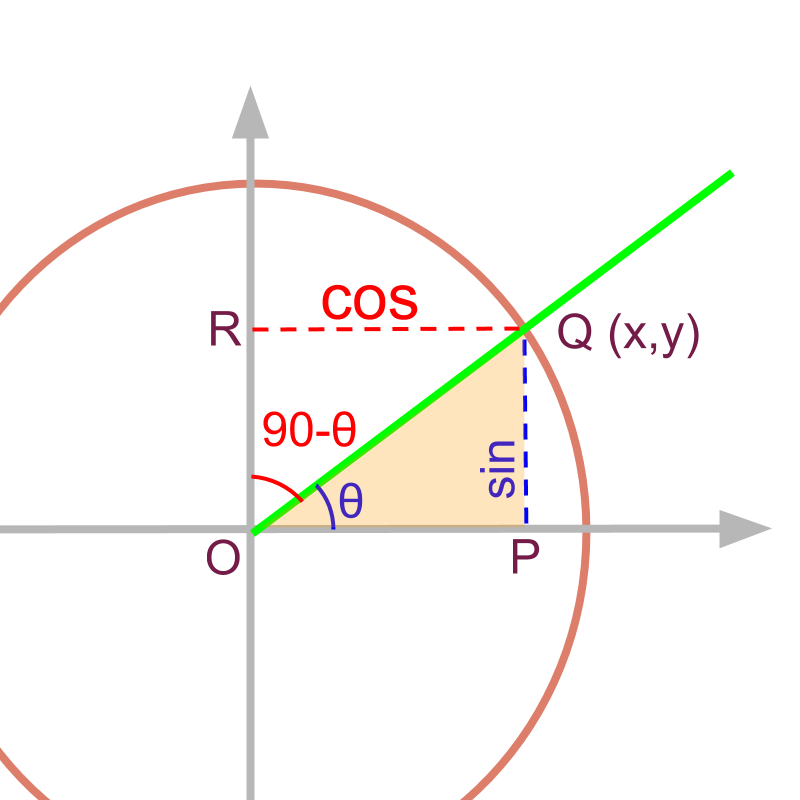
Given that the point $Q$ $Q$ is $(x, y)$ $(x,y)$ ,

$\cos θ = x$ $cos theta = x$

$\cos θ$ $cos theta$ is the projection on x-axis for the line of unit length at angle $θ$ $theta$ .

line touching the circle

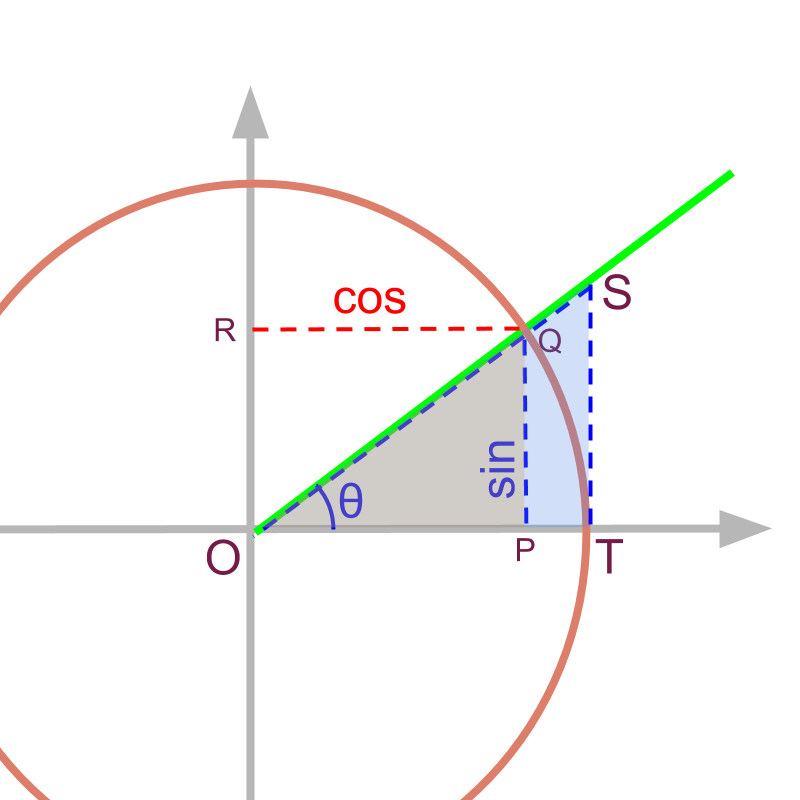
Consider two triangles $O P Q$ $OPQ$ and $O T S$ $OTS$ . It is noted that $\bar{T S}$ $bar(TS)$ is a tangent to the circle.

The triangles $△ O P Q$ $/_\ OPQ$ and $△ O T S$ $/_\ OTS$ are similar right-angled-triangles. And $\bar{O T} = \bar{O Q} = 1$ $bar(OT)=bar(OQ)=1$ as it is unit circle.

ratios of sides of similar triangles are equal
$\bar{S T} \div \bar{O T} = \bar{P Q} \div \bar{O P}$ $bar(ST) -: bar(OT) = bar(PQ) -: bar(OP)$

substituting $\bar{O T} = 1$ $bar(OT)=1$ , $\bar{P Q} = \sin θ$ $bar(PQ) = sin theta$ and $\bar{O P} = \cos θ$ $bar(OP)=cos theta$
$\bar{S T} = \frac{\sin θ}{\cos θ}$ $bar(ST) = (sin theta)/(cos theta)$
$\bar{S T} = \tan θ$ $bar(ST) = tan theta$

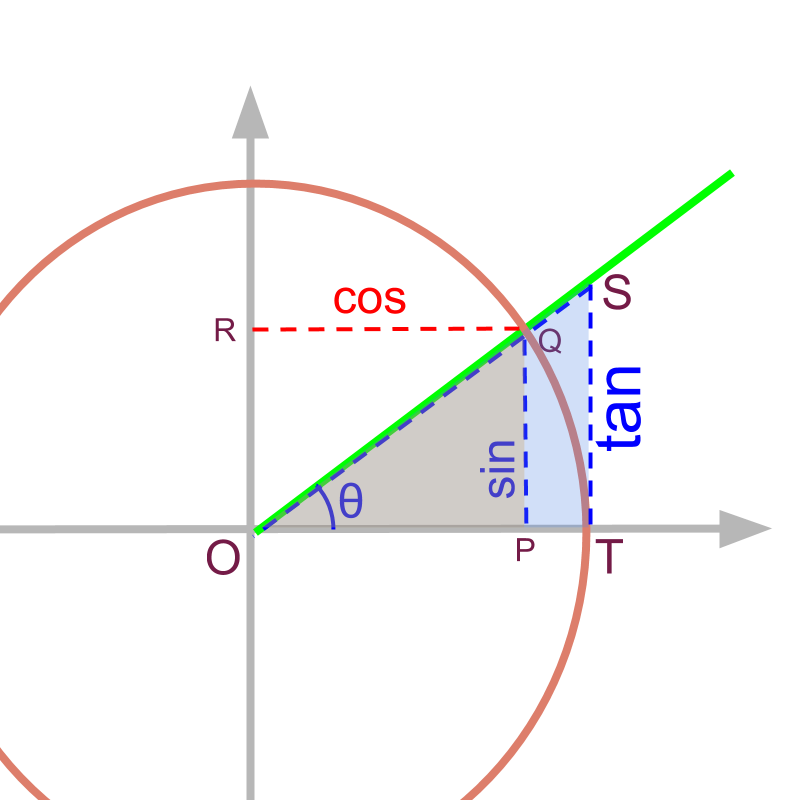
For a given angle $θ$ $theta$ , the $\tan θ$ $tan theta$ is the length of the line segment on tangent as shown in figure.

$\tan$ $tan$ is the short form of 'tangent'.

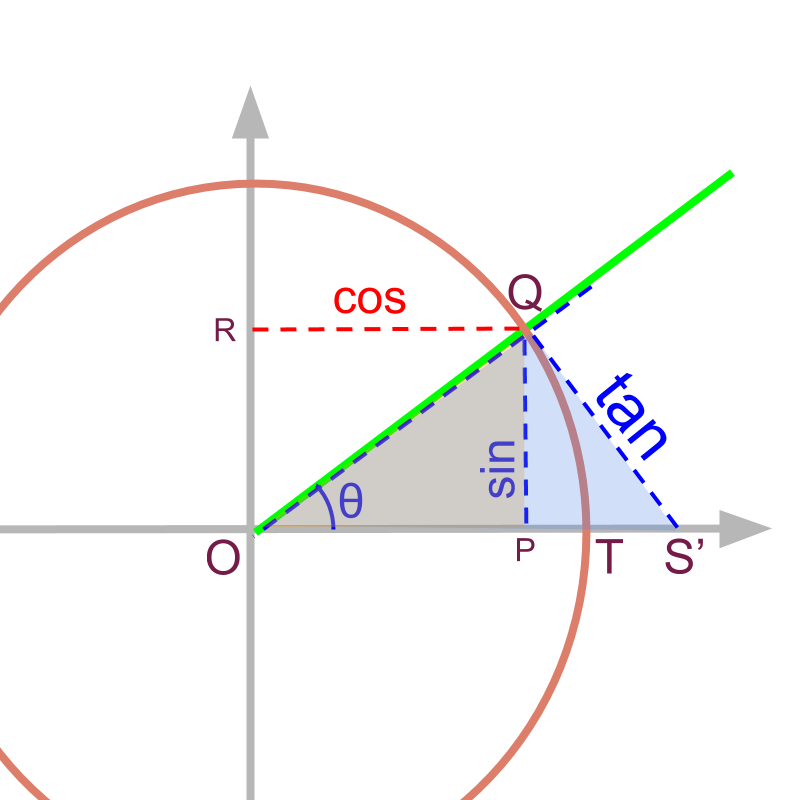
The $\tan$ $tan$ of an angle is equivalently given as $\bar{Q S'}$ $bar(QS′)$ as shown in figure.

Note the following:
$△ O P Q$ $/_\ OPQ$ and $△ O Q S'$ $/_\ OQS′$ are similar triangles and so
$\frac{\bar{Q S'}}{\bar{O Q}} = \frac{\bar{P Q}}{\bar{O P}}$ $bar(QS′)/bar(OQ) = bar(PQ)/bar(OP)$
so, $\tan θ = \frac{\bar{P Q}}{\bar{O P}}$ $tan theta = bar(PQ)/bar(OP)$

line cutting the circle

Consider the line $\bar{S' S}$ $bar(S′S)$ . It is a secant to the circle.

Consider the circle with part of the secant $O S$ $OS$

$△ O P Q$ $/_\ OPQ$ and $△ O Q S$ $/_\ OQS$ are similar right angled triangles.
So $hypotenuse \div adjacent$ $text (hypotenuse) -: text(adjacent)$ for the triangles are equal.

$\bar{O S} \div \bar{O Q} = \bar{O Q} \div \bar{O P}$ $bar(OS) -: bar(OQ) = bar(OQ) -: bar(OP)$

Substitute $\bar{O Q} = 1$ $bar(OQ) = 1$ , and $\bar{O P} = \cos θ$ $bar(OP) = cos theta$

the line segment
$\bar{O S}$ $bar(OS)$
$= \frac{1}{\cos θ}$ $= 1\/(cos theta)$
$= \sec θ$ $= sec theta$

The trigonometric value corresponding to $\bar{O S}$ $bar(OS)$ is $\sec θ$ $sec theta$ .

$\sec θ = \frac{1}{\cos θ} = \frac{1}{x}$ $sec theta = 1/(cos theta) = 1/x$

cosecant

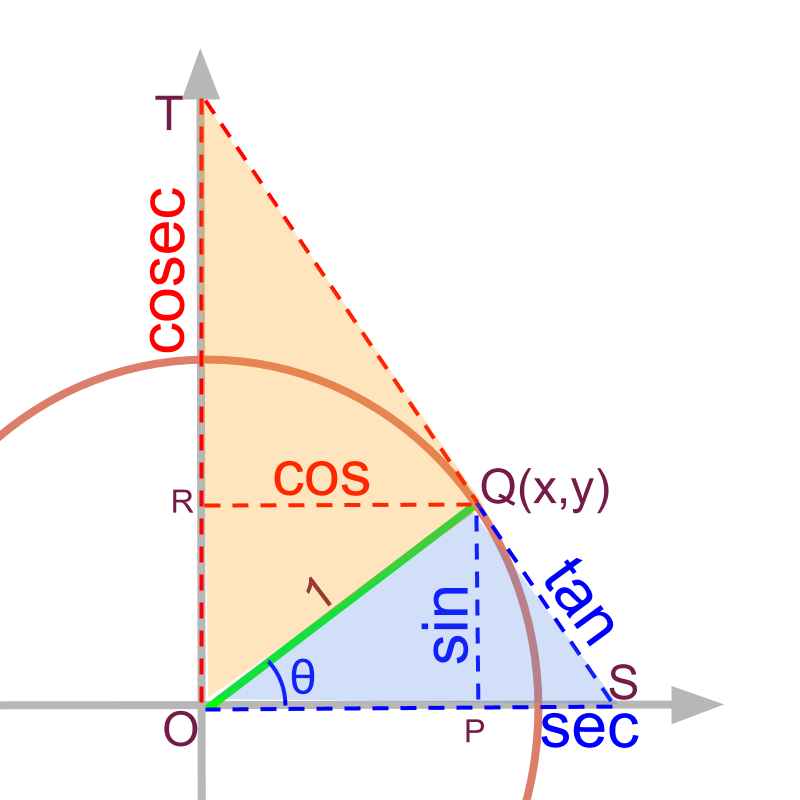
The secant for the complementary angle of theta is $\bar{O T}$ $bar(OT)$ as given in the figure. It is noted that $△ T Q O$ $/_\ TQO$ and $△ O P Q$ $/_\ OPQ$ are similar right-angled-triangles.

Ratio of corresponding sides are equal $\frac{\bar{O T}}{\bar{O Q}} = \frac{\bar{O Q}}{\bar{P Q}}$ $bar(OT)/bar(OQ) = bar(OQ)/bar(PQ)$

substitute $\bar{O Q} = 1$ $bar(OQ) = 1$ and $\bar{P Q} = \sin θ$ $bar(PQ) = sin theta$

The line segment $\bar{O T}$ $bar(OT)$

$= \frac{1}{\sin θ}$ $= 1/(sin theta)$

$= cosec θ or \csc θ$ $= text(cosec) theta text( or ) csc theta$

The trigonometric value corresponding to $\bar{O T}$ $bar(OT)$ is $cosec θ$ $text(cosec) theta$ .

$cosec θ = \frac{1}{\sin θ} = \frac{1}{y}$ $text(cosec) theta = 1/(sin theta) = 1/y$

cotangent

The tangent for the complementary angle of theta is $\bar{Q T}$ $bar(QT)$ as given in the figure.

It is noted that $△ T Q O$ $/_\ TQO$ and $△ O P Q$ $/_\ OPQ$ are similar right-angled-triangles.

ratio of corresponding sides are equal $\frac{\bar{Q T}}{\bar{O Q}} = \frac{\bar{O P}}{\bar{P Q}}$ $bar(QT)/bar(OQ) = bar(OP)/bar(PQ)$

substitute $\bar{O Q} = 1$ $bar(OQ) = 1$ , $\bar{P Q} = \sin θ$ $bar(PQ) = sin theta$ and $\bar{O P} = \cos θ$ $bar(OP) = cos theta$ .

The $\bar{Q T}$ $bar(QT)$

$= \frac{\cos θ}{\sin θ}$ $=(cos theta)/(sin theta)$

$= \cot θ$ $=cot theta$

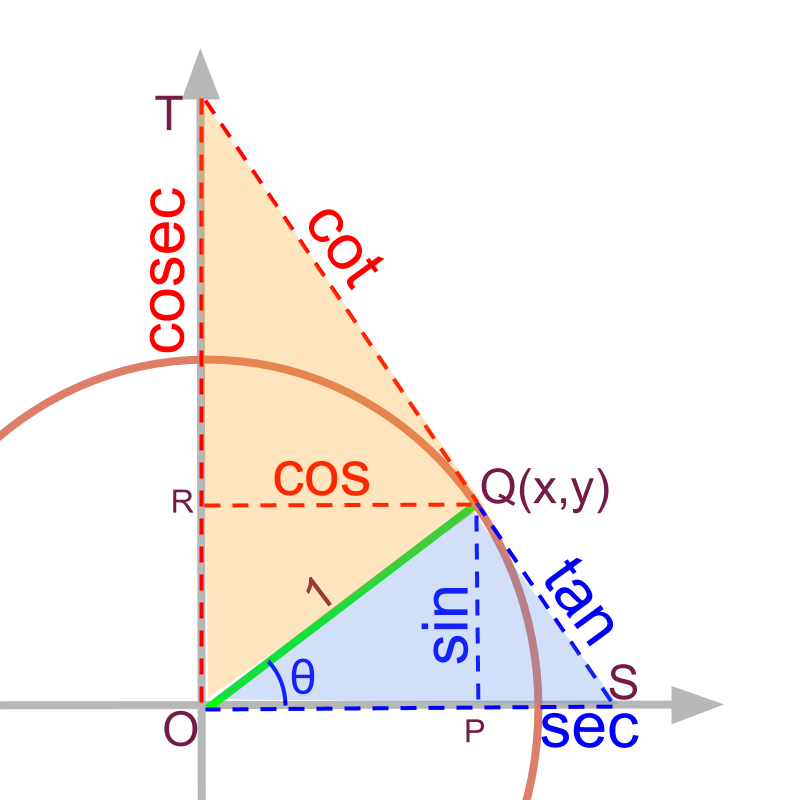
The trigonometric value corresponding to $\bar{Q T}$ $bar(QT)$ is $\cot θ$ $cot theta$ .

$cot θ = \frac{1}{\tan θ} = \frac{\cos θ}{\sin θ} = \frac{x}{y}$ $text(cot) theta = 1/(tan theta) = (cos theta)/(sin theta) = x/y$

trigonometric values

The trigonometric values for a given angle $θ$ $theta$ is defined as lengths in relation to

• chord or sine : $\sin θ$ $sin theta$

• tangent : $\tan θ$ $tan theta$

• secant : $\sec θ$ $sec theta$

all the above for complementary angle

• co-sine : $\cos θ$ $cos theta$

• co-tangent : $\cot θ$ $cot theta$

• co-secant : $\csc θ$ $csc theta$ or $cosec θ$ $text(cosec) theta$

summary

Trigonometric Values: For a line segment of unit length at the angle $θ$ $theta$

The point on unit circle for given angle $θ$ $theta$ is $P (x, y)$ $P(x,y)$ .

Note: $x$ $x$ and $y$ $y$ are the projections on $x$ $x$ -axis and $y$ $y$ -axis.

• chord or sine : $\sin θ = y$ $sin theta = y$

• tangent : $\tan θ = \frac{y}{x}$ $tan theta = y/x$

• secant : $\sec θ = \frac{1}{x}$ $sec theta = 1/x$

For complementary-angle

• co-sine : $\cos θ = x$ $cos theta = x$

• co-tangent : $\cot θ = \frac{x}{y}$ $cot theta = x/y$

• co-secant : $\csc θ$ $csc theta$ or $cosec θ = \frac{1}{y}$ $text(cosec) theta = 1/y$

Outline

It is advised to do the firmfunda version of "basics of Trigonometry" course before doing this.

The outline of material to learn "Advanced Trigonometry" is as follows.
Note: go to detailed outline of Advanced Trigonometry

→ Unit Circle form of Trigonmetric Values

→ Trigonometric Values in all Quadrants

→ Trigonometric Values or any Angles : First Principles

→ Understanding Trigonometric Values in First Quadrant

→ Trigonometric Values in First Quadrant

→ Trigonometric Values of Compound Angles: Geometrical Proof

→ Trigonometric Values of Compound Angles: Algebraic Proof

→ Trigonometric Values of Compound Angles: tan cot

→ Trigonometric Values of Compound Angles: more results