Trigonometry (advanced) : Trigonometric Values in Four Quadrants

maths > advanced-trigonometry

Trigonometric Values in Four Quadrants

what you'll learn...

Trigonometric Values : Angles in Any Quadrant

» The angle $ω$ $omega$ is measured from positive x-axis
      x and y coordinates takes sign. 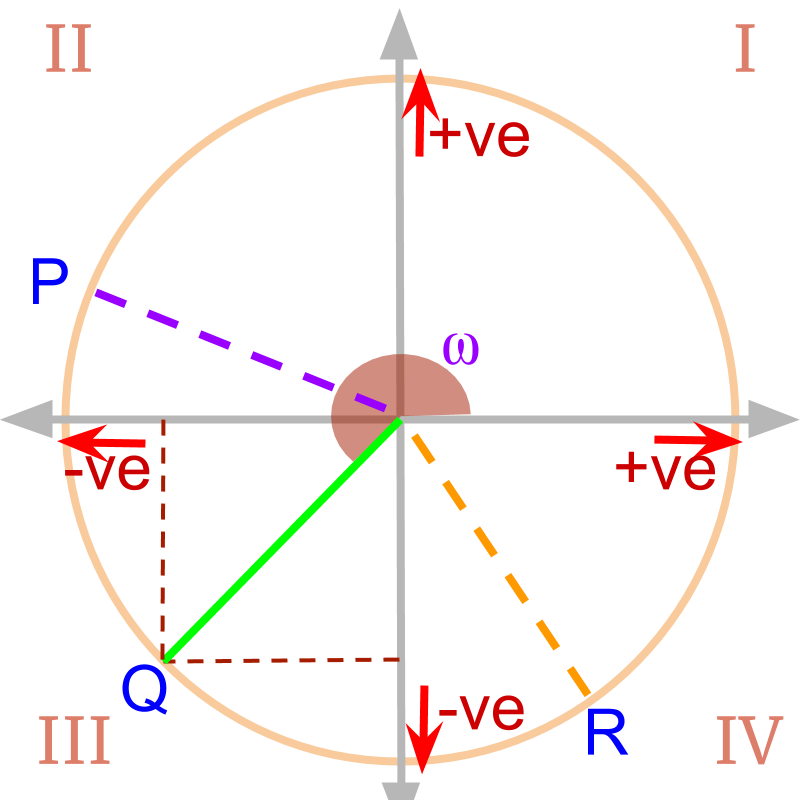angles in quandrant » Trigonometric values can be derived for points $P$ $P$ , $Q$ $Q$ , and $R$ $R$
      $\sin θ = y$ $sin theta = y$
      $\cos θ = x$ $cos theta = x$

quad means four

2D coordinate plane is split into four quadrants. Four Quadrants are numbered as I, II, III, and IV as shown in the figure.

The word "quadrant" means quarter of a plane. The word "Quadrant" is derived from one fourth or quarter.

angles in other quadrants

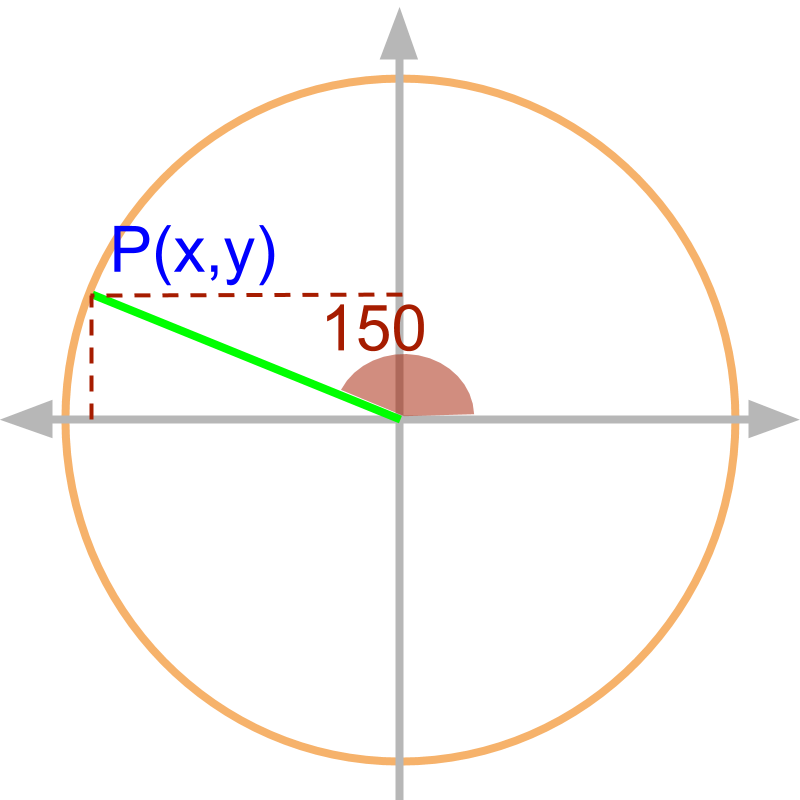
Consider angle $150^{\circ}$ $150^@$ . ${\sin 150}^{\circ}$ $sin 150^@$ can be computed for line on unit circle at $∠ 150^{\circ}$ $/_150^@$ . The projection of the line on x and y axes defines the trigonometric ratios.

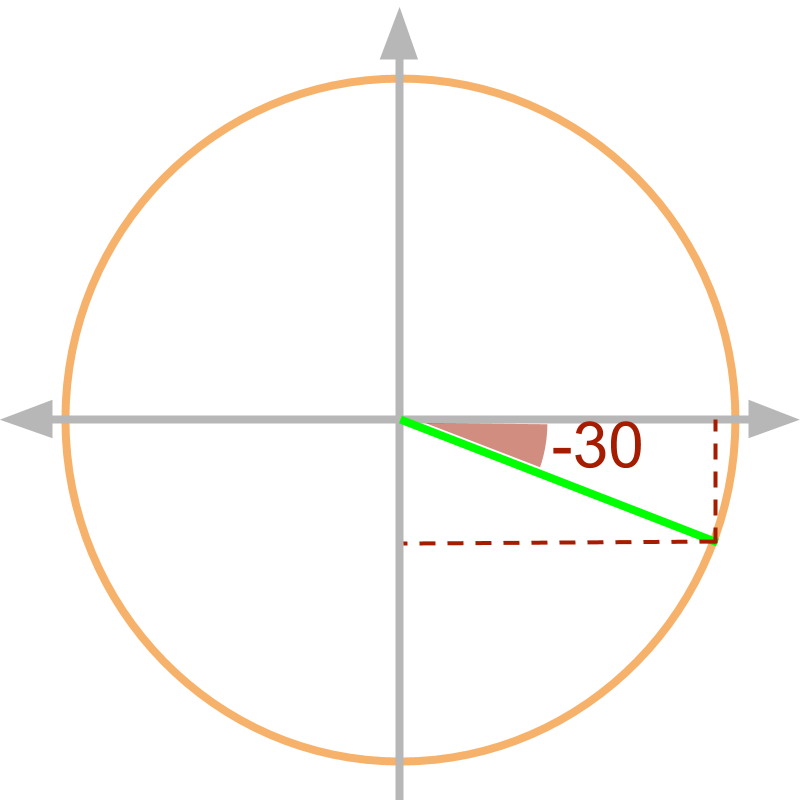
trigonometric ratios for negative angles

Similarly, $\sin (- 30^{\circ})$ $sin(-30^@)$ can be computed for line of unit circle at $- 30^{\circ}$ $-30^@$ angle. The projection of the line on x and y axes defined the trigonometric ratios.

positive and negative

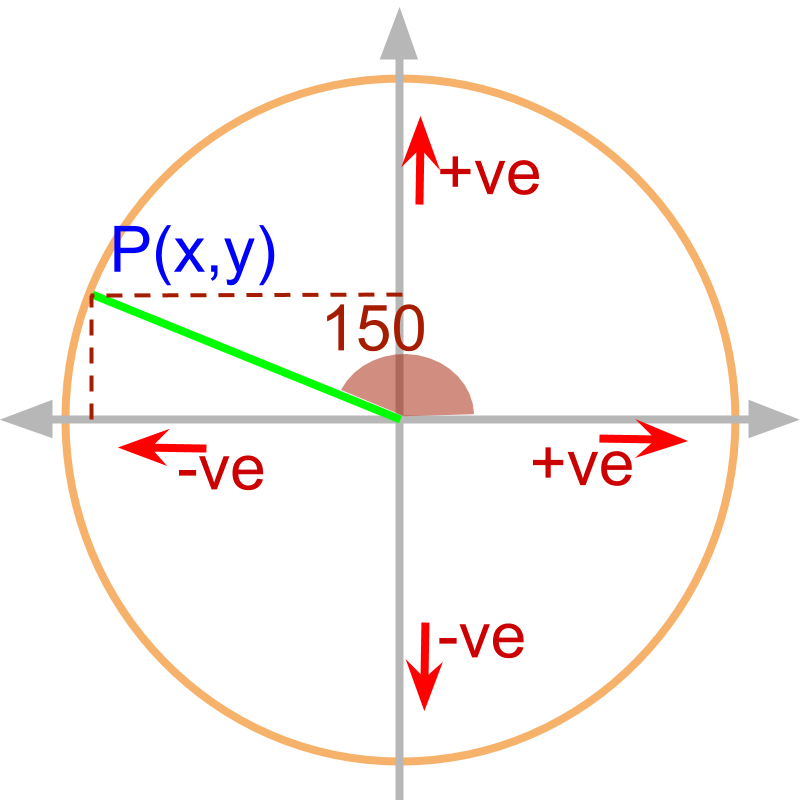
trigonometric ratios negative or positive

The projection of line on x and y axes can be positive or negative. So the trigonometric ratios can be positive or negative.

Trigonometric Ratios can be calculated for any angle between $- \infty$ $-oo$ and $\infty$ $oo$ and the value of ratio can be positive or negative.

summary

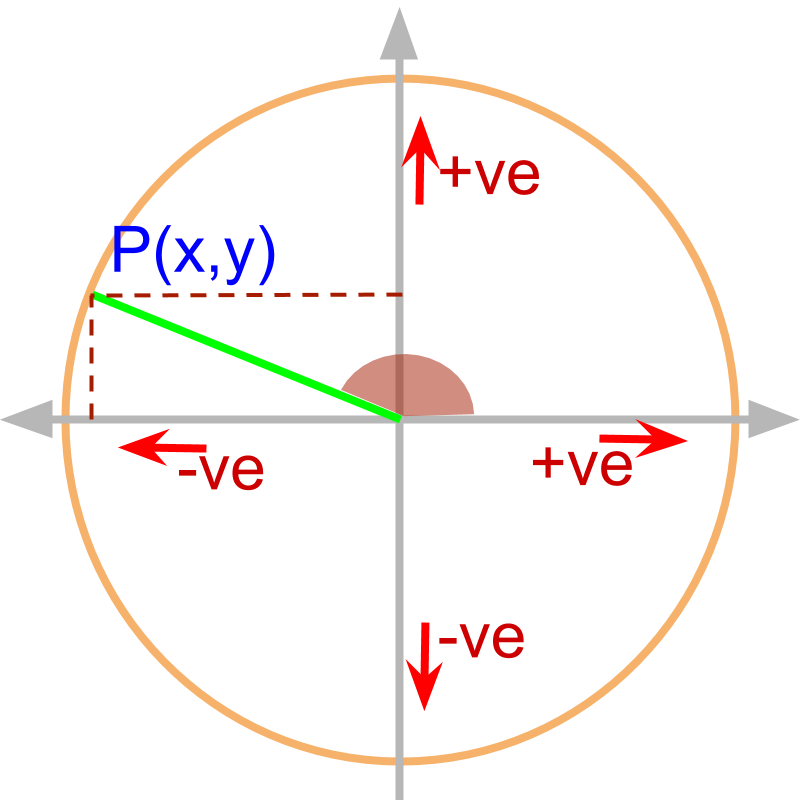
Understanding Trigonometric Ratios for any Angle: Consider the line at the given angle in the unit circle. The projections on x and y axes define the trigonometric ratios. The angle can be between $- \infty$ $-oo$ and $\infty$ $oo$ and the projections can be positive or negative.

Outline

It is advised to do the firmfunda version of "basics of Trigonometry" course before doing this.

The outline of material to learn "Advanced Trigonometry" is as follows.
Note: go to detailed outline of Advanced Trigonometry

→ Unit Circle form of Trigonmetric Values

→ Trigonometric Values in all Quadrants

→ Trigonometric Values or any Angles : First Principles

→ Understanding Trigonometric Values in First Quadrant

→ Trigonometric Values in First Quadrant

→ Trigonometric Values of Compound Angles: Geometrical Proof

→ Trigonometric Values of Compound Angles: Algebraic Proof

→ Trigonometric Values of Compound Angles: tan cot

→ Trigonometric Values of Compound Angles: more results