
what you'll learn...
From 2nd to 1st Quadrant
 »
»
→ measured with y axis
→ complementary functions
 »
»
→ measured with x axis
→ equivalent functions
From 3rd to 1st Quadrant
 »
»
→ measured with x axis
→ equivalent functions
 »
»
→ measured with y axis
→ complementary functions
From 4th to 1st Quadrant
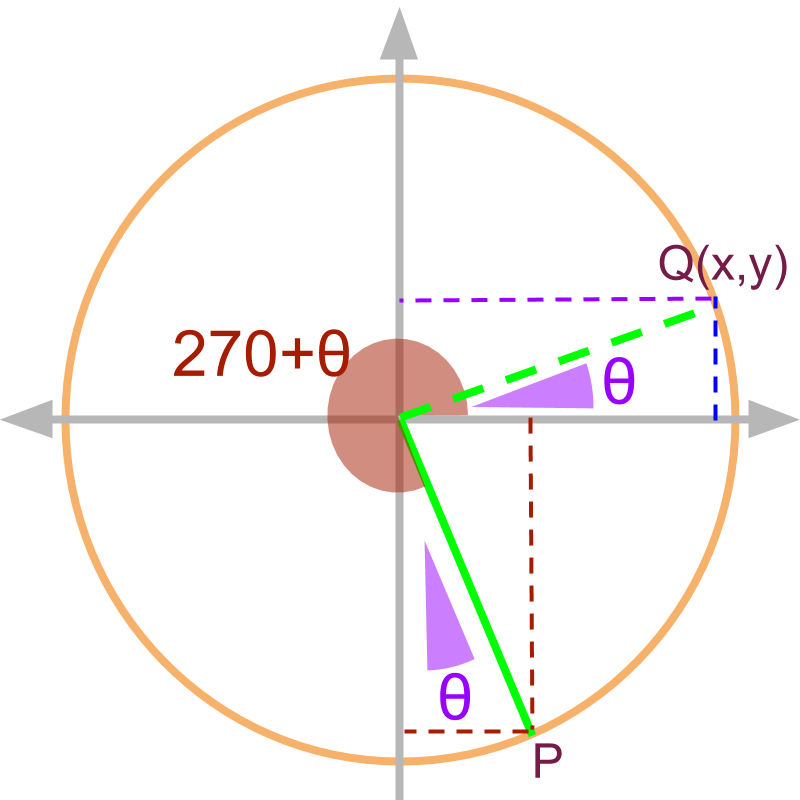 »
»
→ measured with y axis
→ complementary functions
 »
»
→ measured with x axis
→ equivalent functions
Complementary Angles 1st Quadrant
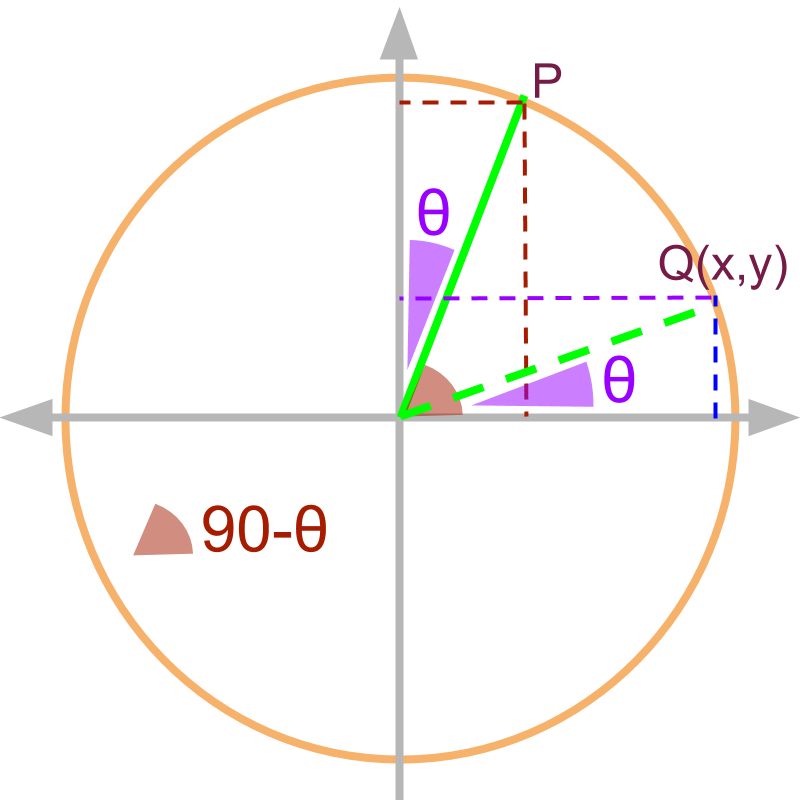 »
»
→ measured with y axis
→ complementary functions
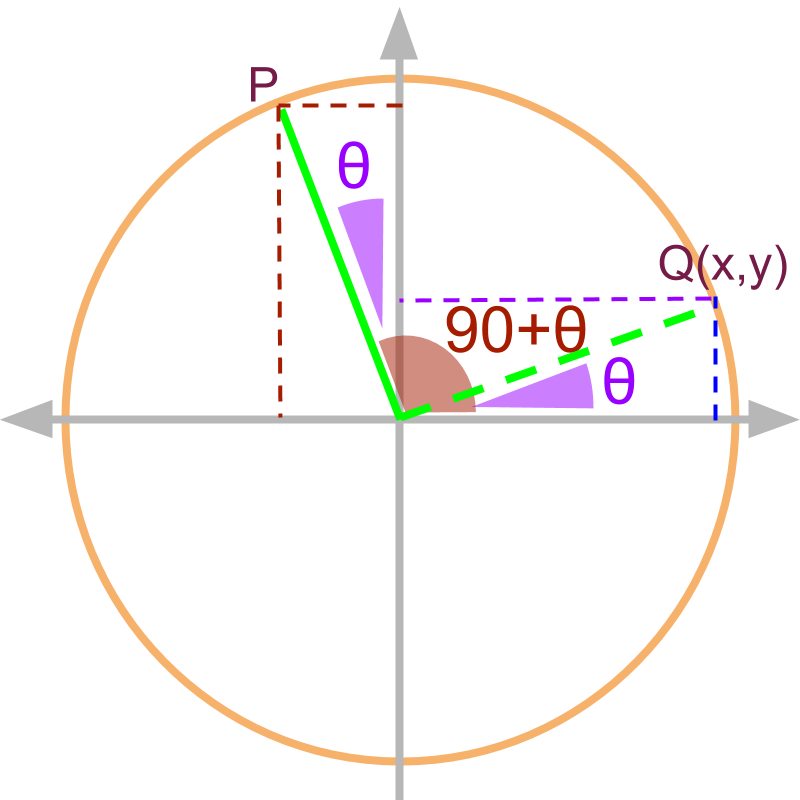
second quadrant

The angle is shown in the figure as point P. The similar triangle with angle theta is given by in 1st quadrant.
Note: Given , the coordinate of is :
and
(tan of the given angle)
(by definition of )
(substituting the values)
(equivalently in 1st quadrant.)
Note: learners can work out this for and .
For angles given as ,
• the angle is in 2nd quadrant, so x projection is negative and y projection is positive.
• the is measured with y-axis, and so the similar triangle in 1st quadrant will have with x-axis, thereby swapping the x and y projections.
the trigonometric ratios are:
•
•
•

The angle is shown in the figure as point P. The similar triangle with is given by in 1st quadrant.
Note: Given , the coordinates of is :
and
(tan of the given angle)
(by definition of )
(substituting the values)
(equivalently in 1st quadrant.)
Note: learners can work out this for and .
summary
For angles given as , the trigonometric ratios are:
•
•
•
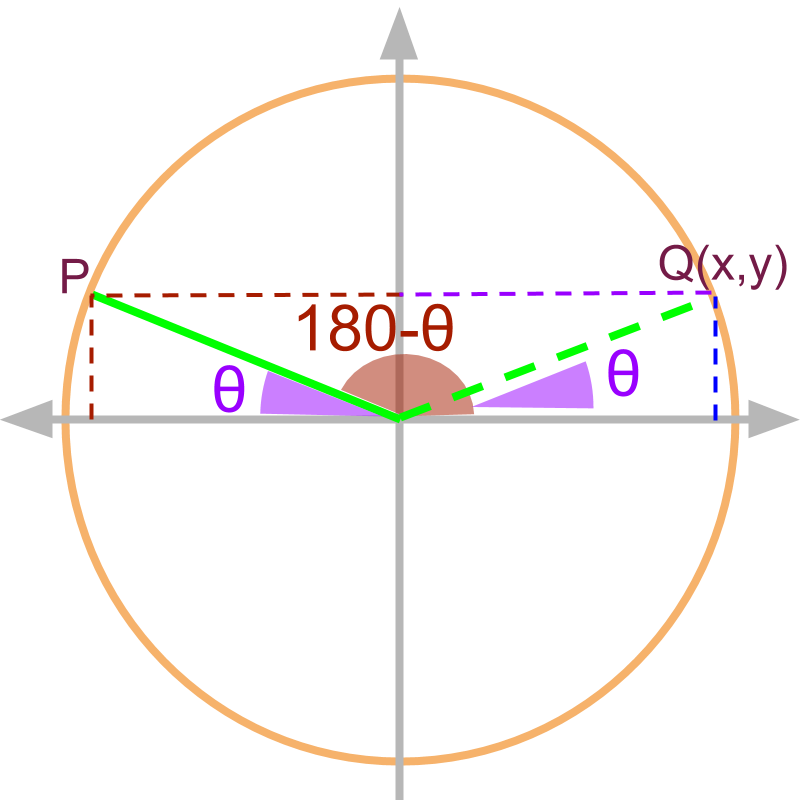
third quadrant

The angle is shown in the figure as point P. The similar triangle with angle theta is given by in 1st quadrant.
Note: Given , the coordinates of is :
and
(tan of the given angle)
(by definition of )
(substituting the values)
(equivalently in 1st quadrant.)
Note: learners can work out this for and .
For angles given as , the trigonometric ratios are:
•
•
•

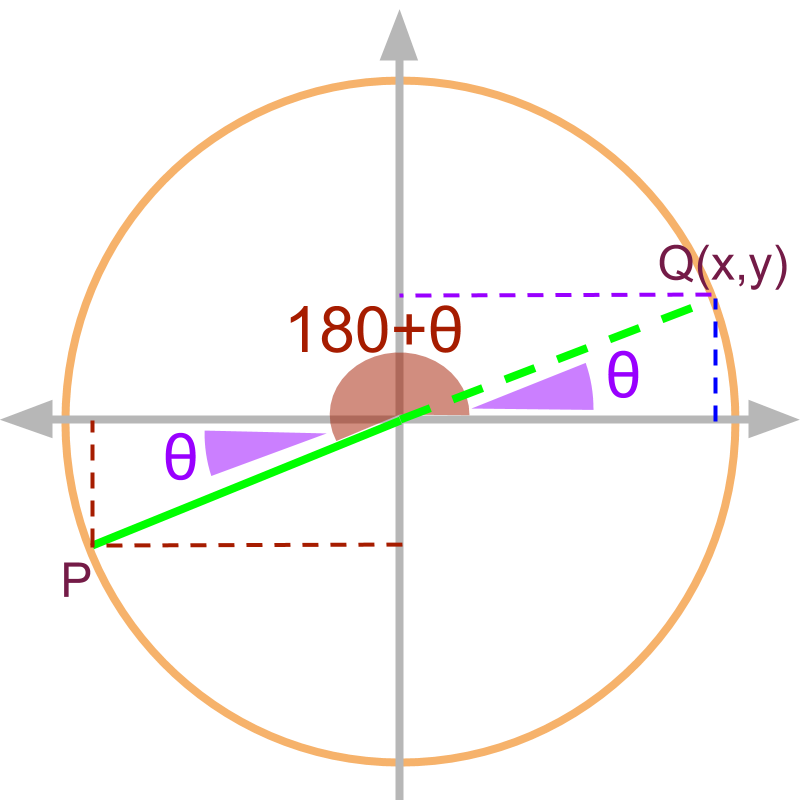
The angle is shown in the figure as point P. The similar triangle with angle theta is given by in 1st quadrant.
Note: Given , the coordinates of is :
and
What is
(tan of the given angle)
(by definition of )
(substituting the values)
(equivalently in 1st quadrant.)
Note: learners can work out this for and .
summary
For angles given as , the trigonometric ratios are:
•
•
•
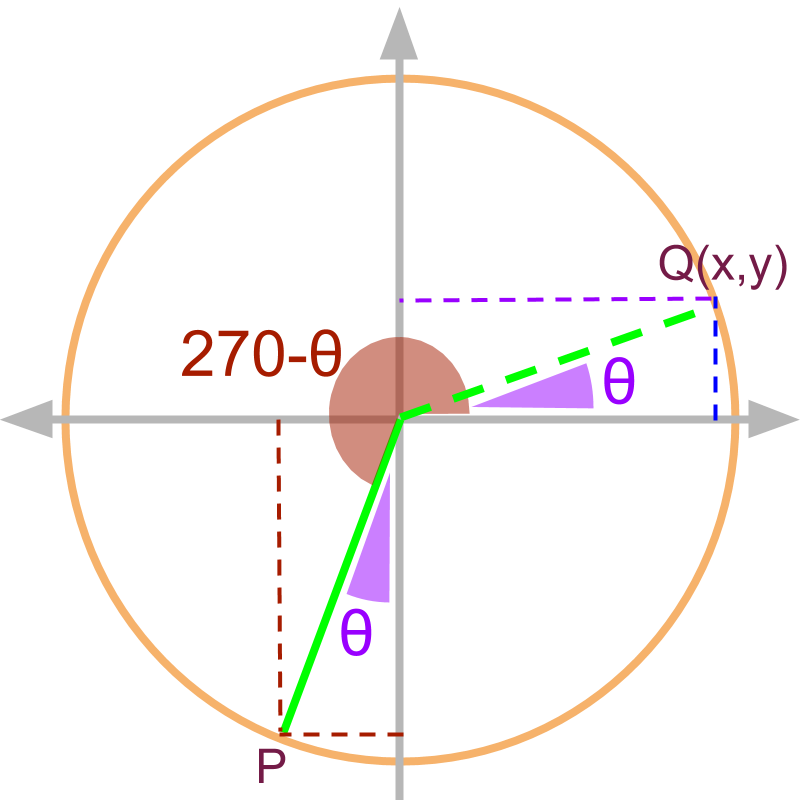
fourth quadrant

The angle is shown in the figure as point P. The similar triangle with angle theta is given by in 1st quadrant.
Note: Given , the coordinates of is :
and
(tan of the given angle)
(by definition of )
(substituting the values)
(equivalently in 1st quadrant.)
Note: learners can work out this for and .
For angles given as , the trigonometric ratios are:
•
•
•

The angle is shown in the figure as point P. The similar triangle with angle theta is given by in 1st quadrant.
Note: Given , the coordinates of is :
and
(tan of the given angle)
(by definition of )
(substituting the values)
(equivalently in 1st quadrant.)
Note: learners can work out this for and .
summary
For angles given as , the trigonometric ratios are:
•
•
•
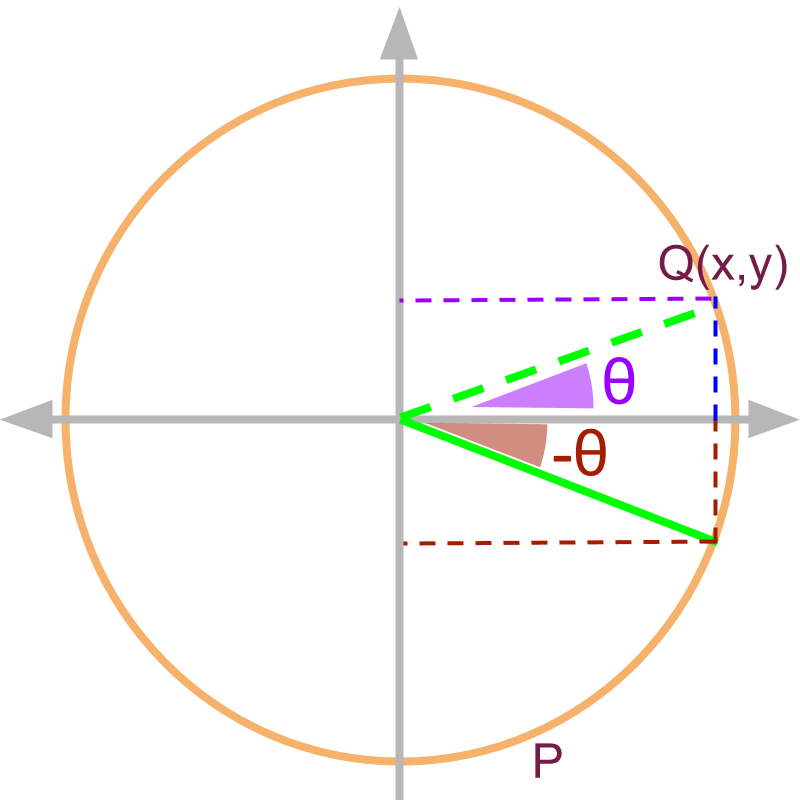
negative angle

The angle is shown in the figure as point P. The similar triangle with angle theta is given by in 1st quadrant.
For angles given as , the trigonometric ratios are:
•
•
•
For angles measured in reference to x axis, the trigonometric ratios remain the same when equivalently represented in the 1st quadrant.
For angles measured in reference to y axis, the trigonometric ratios are equivalently complementary ratios in the 1st quadrant.
summary
Trigonometric Ratios in 1st Quadrant:
For Angles in reference to x-axis:
For Angles in reference to y-axis:
Outline
It is advised to do the firmfunda version of "basics of Trigonometry" course before doing this.
The outline of material to learn "Advanced Trigonometry" is as follows.
Note: go to detailed outline of Advanced Trigonometry
→ Unit Circle form of Trigonmetric Values
→ Trigonometric Values in all Quadrants
→ Trigonometric Values or any Angles : First Principles
→ Understanding Trigonometric Values in First Quadrant
→ Trigonometric Values in First Quadrant
→ Trigonometric Values of Compound Angles: Geometrical Proof
→ Trigonometric Values of Compound Angles: Algebraic Proof
→ Trigonometric Values of Compound Angles: tan cot
→ Trigonometric Values of Compound Angles: more results