Trigonometry (advanced) : First Quadrant Equivalent of Trigonometric Values

maths > advanced-trigonometry

First Quadrant Equivalent of Trigonometric Values

what you'll learn...

Conversion to 1st Quadrant

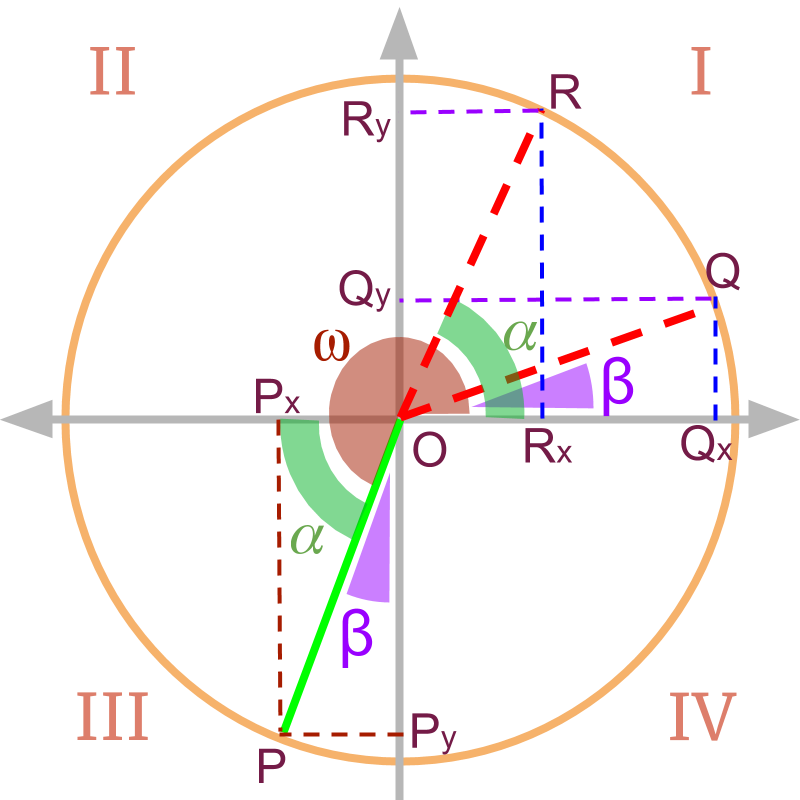» Conversion of angle $ω$ $omega$ to 1st quadrant
    → acute angle made by point $P$ $P$ with x axis $α$ $alpha$
    → acute angle made by point $P$ $P$ with y axis $β$ $beta$

» Point $R$ $R$ makes angle $α$ $alpha$ in 1st quadrant.
    → $R_{x} = P_{x}$ $R_x = P_x$
    → $R_{y} = P_{y}$ $R_y = P_y$
    → x and y coordinates position is retained
    → $\sin ω = \pm \sin α$ $sin omega = +- sin alpha$
    → $\cos ω = \pm \cos α$ $cos omega = +- cos alpha$

» Point $Q$ $Q$ makes angle $β$ $beta$ in 1st quadrant.
    → $Q_{x} = P_{y}$ $Q_x = P_y$
    → $Q_{y} = P_{x}$ $Q_y = P_x$
    → x and y coordinates position is interchanged
    → $\sin ω = \pm \cos β$ $sin omega = +- cos beta$
    → $\cos ω = \pm \sin β$ $cos omega = +- sin beta$

Quickly follow the x and y projection in the quadrant to figure out the conversion. No need to memorize.

understanding the problem

We studied about angles that are in 2nd, 3rd, or 4th quadrants. Before that, We have studied about trigonometric ratios for standard angles $0, 30, 45, 60, 90$ $0, 30, 45, 60, 90$ degree, which are all in 1st quadrant.

Are there more standard angles in the 2nd, 3rd, or 4th quadrants? Should one learn the values of such angles?

Or can the trigonometric ratios of angles from 2nd, 3rd, and 4th quadrants be equivalently represented with trigonometric ratios of angles from 1st quadrant only. If such transformation is possible, then it simplifies.

Note: For any angle in 2nd, 3rd, and 4th quadrants, trigonometric ratios can be equivalently given as a trigonometric ratios in 1st quadrants. The objective of this page is to learn that.

two contexts

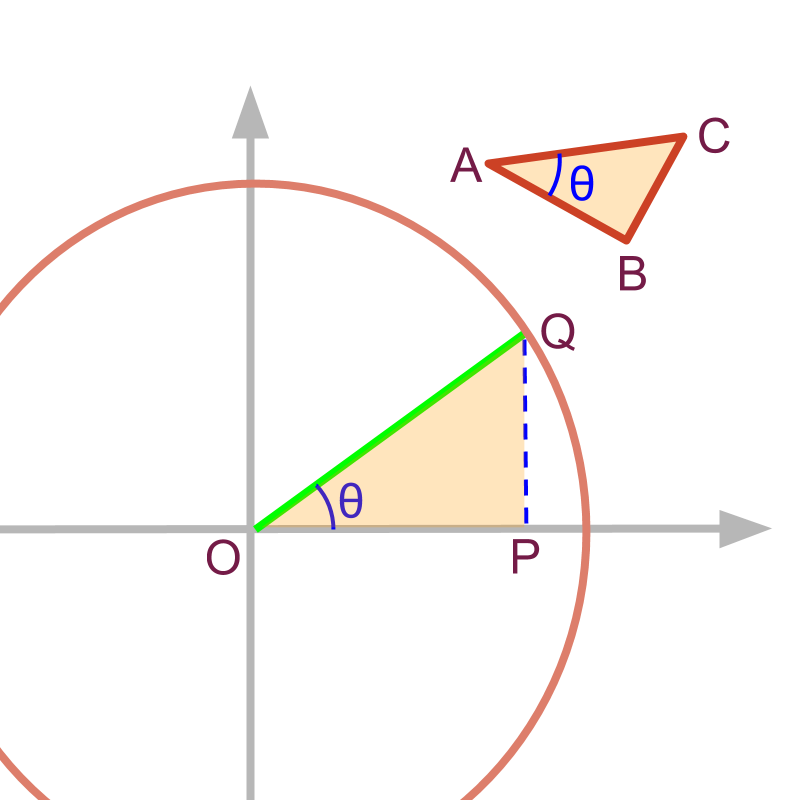
trigonometric ratios of triangles equivalently in 1st quadrant

Trigonometric ratios can be defined in two contexts

• For a right-angled-triangle with angle $θ$ $theta$ , the hypotenuse and sides of the triangle define the ratios

• In a unit circle, the line at the given angle $θ$ $theta$ forms a similar triangle and ratios can be equivalently given in that triangle.

two forms in unit-circle

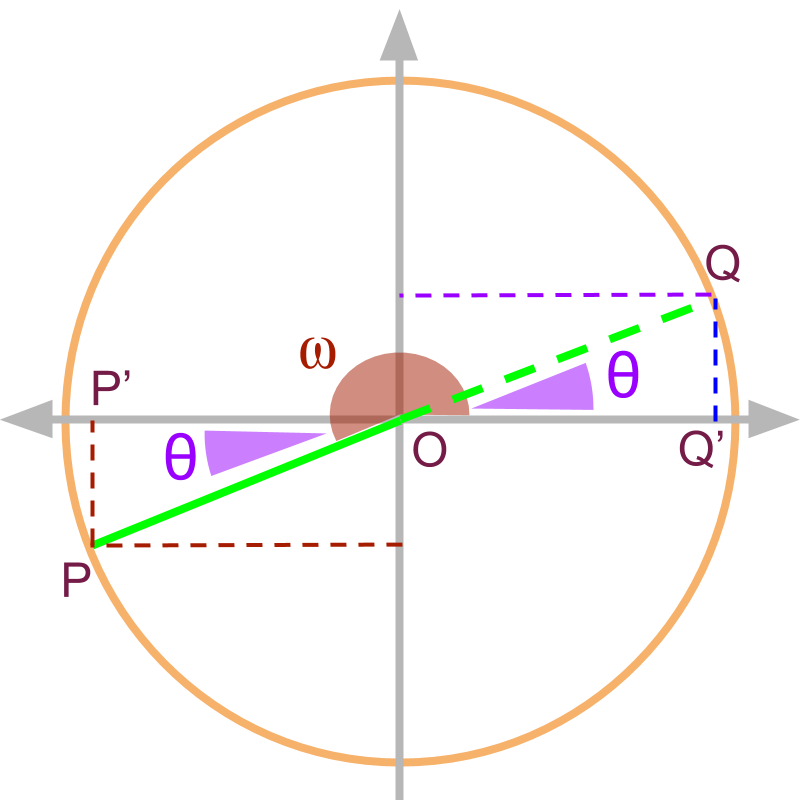
trigonometric ratios of angles equivalently in 1st quadrant

For a given $∠ ω$ $/_ omega$ , the trigonometric ratios can be defined in two forms the projections on x and y axis for the given $∠ ω$ $/_ omega$ an equivalent ratio for the $∠ θ$ $/_theta$ in the first quadrant. Note, $△ O Q' Q$ $/_\ OQ′Q$ is a similar triangle to $△ O P' P$ $/_\ OP′P$ and so the trigonometric ratios of $∠ ω$ $/_ omega$ can be specified in terms of $∠ θ$ $/_ theta$ .

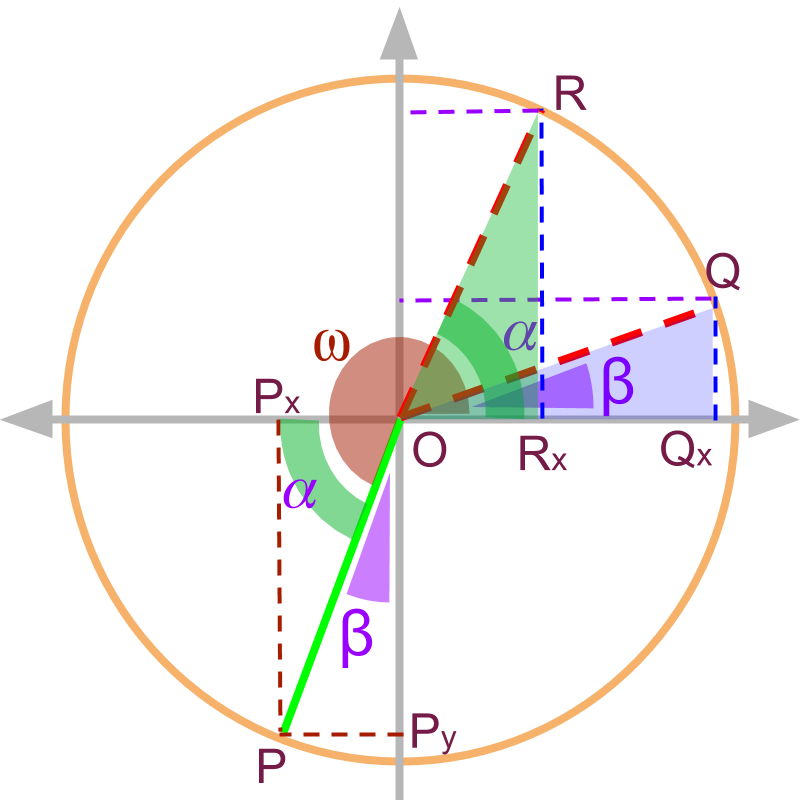
Note the following for $∠ ω$ $/_omega$ the point on unit circle is $P$ $P$ and its x and y projections are $P_{x}$ $P_x$ and $P_{y}$ $P_y$ .

The angle $\bar{O P}$ $bar(OP)$ makes with x axis is $α$ $alpha$ and with y axis is $β$ $beta$ .

Two triangles are constructed in the 1st quadrant.

For the angle $α$ $alpha$ the similar triangle in 1st quadrant is $△ O R_{x} R$ $/_\ OR_xR$ .

For the angle $β$ $beta$ the similar triangle in 1st quadrant is $△ O Q_{x} Q$ $/_\ OQ_xQ$

Note that $\bar{O R_{x}} = \bar{O P_{x}}$ $bar(OR_x) = bar(OP_x)$ and $\bar{O Q_{x}} = \bar{O P_{y}}$ $bar(OQ_x) = bar(OP_y)$

The trigonometric ratios of $∠ ω$ $/_omega$ can be found from either one of the following.

$△ O R_{x} R$ $/_\ OR_xR$ as the x and y projections match with that of $P$ $P$ .

$△ O Q_{x} Q$ $/_\ OQ_xQ$ can be used knowing that the x and y projections are interchanged in the 1st quadrant.

For any angle $∠ ω$ $/_omega$ there are two possible similar triangles in 1st quadrant.

First is based on angle made with x-axis, given as $∠ α$ $/_alpha$ , in which case the x and y projections are retained in magnitude in the 1st quadrant. So the trigonometric ratios are retained in the 1st quadrant.
Second is based on angle made with y-axis given as $∠ β$ $/_beta$ , in which case the x and y projections are interchanged in magnitude in the 1st quadrant. So the trigonometric ratios are given for complementary angles.
It is also noted that $∠ α$ $/_alpha$ and $∠ β$ $/_beta$ are complementary angles.

first form: angle with x-axis

trigonometric ratio of all quadrants angle with x axis

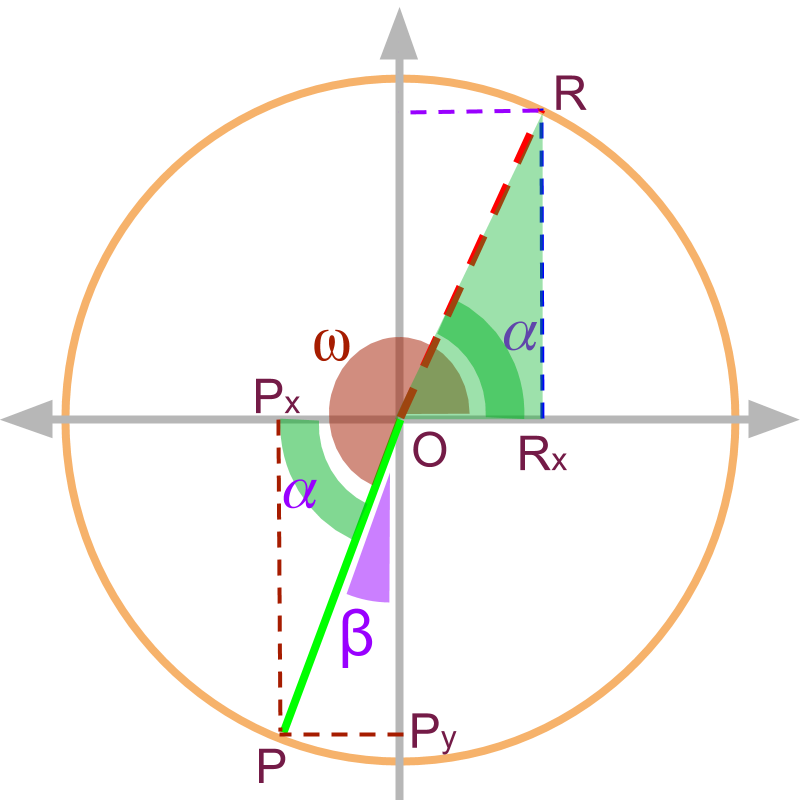
For the $∠ ω$ $/_omega$ , the angle with x-axis $∠ α$ $/_alpha$ is used to construct the similar triangle in the 1st quadrant.

The sign of the trigonometric ratio is derived from the signs of $P_{x}$ $P_x$ and $P_{y}$ $P_y$ .

The trigonometric ratios are

• $\sin ω$ $sin omega$
   $= (sign of y proj.) \times \sin α$ $quad quad = text((sign of y proj.)) xx sin alpha$

• $\cos ω$ $cos omega$
   $= (sign of x proj.) \times \cos α$ $quad quad = text((sign of x proj.)) xx cos alpha$

• $\tan ω$ $tan omega$
   $= \frac{sign of y proj.}{sign of x proj.} \times \tan α$ $quad quad = text(sign of y proj.)/ text(sign of x proj.) xx tan alpha$

first form: angle with y-axis

trigonometric ratio of all quadrants angle with y axis

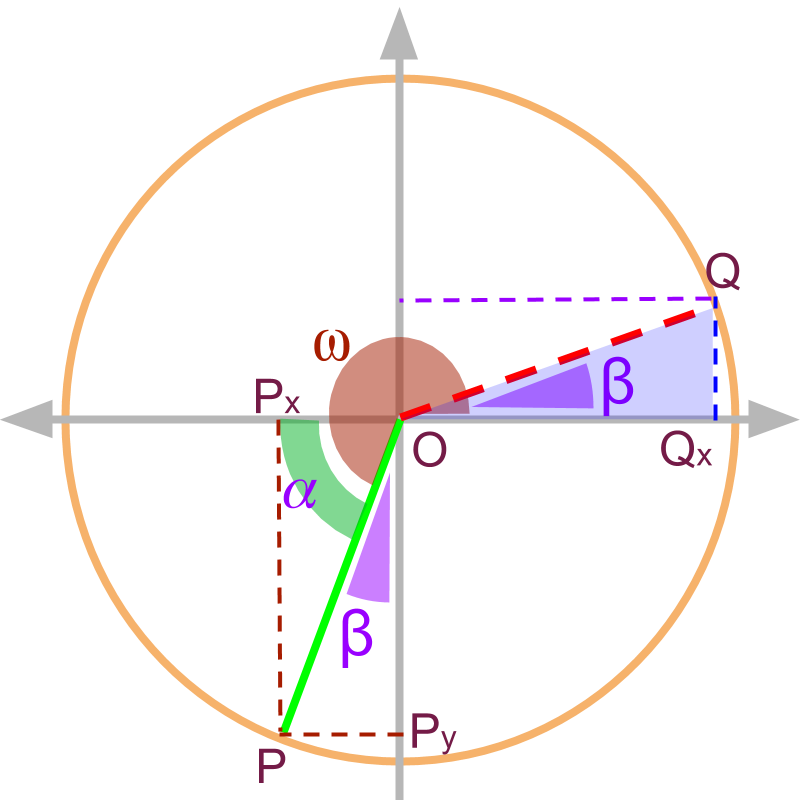
For the $∠ ω$ $/_omega$ , the angle with y-axis $∠ β$ $/_ beta$ is used to construct the similar triangle in the 1st quadrant.

The sign of the trigonometric ratio is derived from the signs of $P_{x}$ $P_x$ and $P_{y}$ $P_y$ .

The trigonometric ratios are

• $\sin ω$ $sin omega$
   $= (sign of y proj.) \times \cos β$ $quad quad = text((sign of y proj.)) xx cos beta$

• $\cos ω$ $cos omega$
   $= (sign of x proj.) \times \sin β$ $quad quad = text((sign of x proj.)) xx sin beta$

• $\tan ω$ $tan omega$
   $= \frac{sign of y proj.}{sign of x proj.} \times \cot β$ $quad quad = text(sign of y proj.)/ text(sign of x proj.) xx cot beta$

remember

The trigonometric ratios of $∠ ω$ $/_omega$ can equivalently be represented with one of the complementary angles $∠ α$ $/_alpha$ and $∠ β$ $/_beta$ in 1st quadrant. Where $∠ α$ $/_alpha$ is the angle with $x$ $x$ -axis and $∠ β$ $/_beta$ is the angle with $y$ $y$ -axis.

The sign of the trigonometric ratios are to be derived from the original quadrant of $∠ ω$ $/_omega$

The $∠ α$ $/_alpha$ maps to equivalent trigonometric ratios as the x and y projections are retained in x and y axes.

The $∠ β$ $/_beta$ maps to complementary trigonometric ratios as the x and y projections are swapped in 1st quadrant.

summary

Equivalent Ratio in 1st Quadrant: Any angle $∠ ω$ $/_omega$ is equivalently considered with either of
• angle made with x-axis $∠ α$ $/_alpha$
• angle made with y-axis $∠ β$ $/_beta$
The equivalent trigonometric value is given in first quadrant.

The trigonometric ratios are

• $\sin ω$ $sin omega$
   $= (sign of y projection) \times \sin α$ $quad quad = text((sign of y projection)) xx sin alpha$
   $= (sign of y projection) \times \cos β$ $quad quad = text((sign of y projection)) xx cos beta$

• $\cos ω$ $cos omega$
   $= (sign of x projection) \times \cos α$ $quad quad = text((sign of x projection)) xx cos alpha$
   $= (sign of x projection) \times \sin β$ $quad quad = text((sign of x projection)) xx sin beta$

• $\tan ω$ $tan omega$
   $= \frac{sign of y proj.}{sign of x proj.} \times \tan α$ $quad quad = text(sign of y proj.)/ text(sign of x proj.) xx tan alpha$
   $= \frac{sign of y proj.}{sign of x proj.} \times \cot β$ $quad quad = text(sign of y proj.)/ text(sign of x proj.) xx cot beta$

Outline

It is advised to do the firmfunda version of "basics of Trigonometry" course before doing this.

The outline of material to learn "Advanced Trigonometry" is as follows.
Note: go to detailed outline of Advanced Trigonometry

→ Unit Circle form of Trigonmetric Values

→ Trigonometric Values in all Quadrants

→ Trigonometric Values or any Angles : First Principles

→ Understanding Trigonometric Values in First Quadrant

→ Trigonometric Values in First Quadrant

→ Trigonometric Values of Compound Angles: Geometrical Proof

→ Trigonometric Values of Compound Angles: Algebraic Proof

→ Trigonometric Values of Compound Angles: tan cot

→ Trigonometric Values of Compound Angles: more results