Integral Calculus : Fundamental Theorem of Calculus

maths > integral-calculus

Fundamental Theorem of Calculus

what you'll learn...

Overview

Fundamental Theorem of Calculus :

For functions $f(x), h(x), g(x)$ as in
$h(x) = d/(dx) f(x)$
$f(x) = int_a^x g(x)dx$

    → First part states that $h(x) = g(x)$ ; that is $d/(dx) int_a^x g(x) dx = g(x)$
derivative of integral of a function is the function

    → First part implies that to find $f(x) = int_a^x g(x)dx$ , find the inverse relationship $d/(dx) f(x) = g(x)$ and thus, anti-derivative is defined.
integral of a function is anti-derivative of the function

    → Second part states that $int_a^b h(x) dx = f(b)-f(a)$
That is $int_a^b d/(dx) f(x) dx = f(b)-f(a)$ .
definite integral of derivative of a function is the difference of function evaluated at the limits

    → Since the second part is true for any value $x$ in the interval $[a,b]$ , it implies that $int_a^x d/(dx) f(x) dx = f(x) +c$ .
indefinite integral of derivative of a function is the function plus an initial value

setting up

This topic is going to be little mathematically involved and firmly anchors some of the concepts in integrals. To prove Fundamental Theorem of Calculus, let us first understand "mean-value-theorem" and "squeeze theorem".

mean value theorem

Mean-Value-Theorem for Derivatives: For a continuous and differentiable function in the closed interval $[a,b]$ , there exists $c$ such that $a<=c<=b$
$d/(dx)f(x)|_(x=c)$ $= (f(b)-f(a)) //(b-a)$
The same can be written as
$f′(c)$ $= (f(b)-f(a)) //(b-a)$

differential mean value theorem The figure graphically explains the mean value theorem :

• $(f(b)-f(a)) //(b-a)$ is illustrated by the slope of hypotenuse of red triangle. In this, numeration and denominator are the two arms of right angle.

• $d/(dx)f(x)|_(x=c)$ is illustrated by the slope of tangent given by orange line. It is noted that. the tangent at $c$ and the hypotenuse shown between $a$ and $b$ have same slope there is at-least one point $c$ in which slope of tangent equals slope of the hypotenuse of red triangle

mean value theorem again

Mean-Value-Theorem for integrals: For a continuous and integrable function in the closed interval $[a,b]$ , there exists $c$ such that $a<=c<=b$
$int_a^b f(x)dx$ $= f(c) xx (b-a)$
The same can be written as
$F(b)-F(a)$ $= f(c) xx (b-a)$
where $F(x)$ is the integral of $f(x)$ , given by $F(x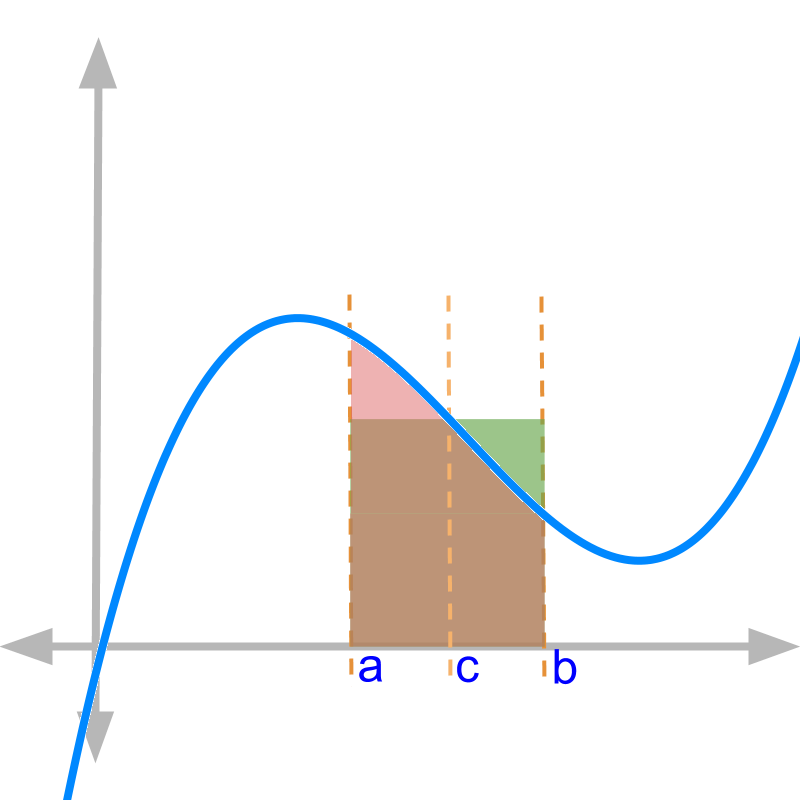) = int_a^x f(x)dx$ . integral mean value theorem The figure graphically explains the mean value theorem:

• $F(b)-F(a)$ is area under the curve shown in red.

• $f(c) xx (b-a)$ is the area of rectangle shown in green.

Area under the curve in red and the area of the rectangle in green are equal

There is at-least one point $c$ in which area of the rectangle equals the area under the curve

Note: There is substantial overlap between red and green area in the figure, shown in dark greyish red color.

The name "mean-value-theorem" provide the clue as to what the theorem is about : one of the values in an interval is the mean for the interval.

squeeze theorem

Squeeze theorem: A value $c$ is given such that $a<=c<=b$ . If $a-b$ tends to $0$ , then $c=a=b$ .

The name of the theorem provide the clue as to what the theorem is about: When an interval $a$ and $b$ is squeezed to $a=b$ , then a value between these two, $c$ , is also squeezed to be equal to the two values.

First part

Given a continuous function $f(x)$ in a closed interval $[a,b]$ and differentiable in open interval $(a,b)$ .
$h(x) = d/(dx) f(x)$
$f(x) = int_a^x g(x)dx$

First part of Fundamental Theorem of Calculus states that $h(x) = g(x)$ ; that is $d/(dx) int_a^x g(x) dx = g(x)$

Note: Derivative of integral of a function is the function.

The above means derivative is the inverse of integral.

First part also implies the abstraction "indefinite integral" or anti-derivatives.
$int g(x)dx = c+ int_0^x g(x)dx$ .
Note that the left hand side is indefinite integral and right hand side involves definite integral.

In indefinite integral, $f(x) = int_a^x g(x)dx$ , the function $f(x)$ is derived from continuous aggregate or, equivalently, by limit of summation.

In anti-derivative, $f(x) +c = int g(x)dx$ , the function $f(x)$ is derived from the inverse operation of derivative. That is, derive $f(x)$ such that, derivative of $f(x)$ is $g(x)$ .

In other words, $f(x) +c = int g(x)dx$ means the anti-derivative of $g(x)$ is $f(x)$ (even though the representation uses integral symbol). The name anti-derivatives is coined to specify this.

Second part

Given a continuous function $f(x)$ in a closed interval $[a,b]$ and differentiable in open interval $(a,b)$ .
$h(x) = d/(dx) f(x)$
$f(x) = int_a^x g(x)dx$

Second part of Fundamental Theorem of Calculus states that $int_a^b h(x) dx = f(b)-f(a)$
That is $int_a^b d/(dx) f(x) dx = f(b)-f(a)$ .

Integral of derivative of a function is the function evaluated at the limits of integral.
(stated for definite integral.)

This implies integral is the inverse of derivative.

Since the second part is true for any value $x$ in the interval $[a,b]$ , it can be given as $int_a^x d/(dx) f(x) dx = f(x) +c$ .

Integral of derivative of a function is the function with a constant of integration.
(stated for indefinite integral.)

This also implies integral is the inverse of derivative.

proof 1

Proof for First part of Fundamental Theorem: Given a continuous function $f(x)$ in a closed interval $[a,b]$ and differentiable in open interval $(a,b)$ .
$h(x) = d/(dx) f(x)$
$f(x) = int_a^x g(x)dx$

First part of Fundamental Theorem of Calculus states that $h(x) = g(x)$ ; that is $d/(dx) int_a^x g(x) dx = g(x)$

$h(x)$

$=d/(dx) f(x)$

substituting definition of differentiation
$= lim_(delta->0) (f(x+delta) - f(x)) / delta$

substituting definition of $f(x)$
$= lim_(delta->0) (int_a^(x+delta) g(x)dx$ $- int_a^(x) g(x)dx) // delta$

$= lim_(delta->0) (int_a^x g(x)dx$ $+ int_x^(x+delta) g(x)dx$ $- int_a^(x) g(x)dx) // delta$

$= lim_(delta->0) (int_x^(x+delta)$ $g(x)dx) // delta$

by mean-value-theorem $int_x^(x+delta) g(x)dx = g(c)delta$ where $x<=c<=x+delta$
$= lim_(delta->0) (g(c)delta) // delta$

canceling non-zero value $delta$
$= lim_(delta->0) g(c)$

by squeeze value theorem: as $delta$ tends to zero, $x<=c<=x+delta$ will imply $c=x$ .
$= g(x)$

The above proves $d/(dx) int_a^x g(x) dx = g(x)$

proof 2

Proof for Second part of Fundamental Theorem: Given a continuous function $f(x)$ in a closed interval $[a,b]$ and differentiable in open interval $(a,b)$ .
$h(x) = d/(dx) f(x)$
$f(x) = int_a^x g(x)dx$

Second part of Fundamental Theorem of Calculus states that $int_a^b h(x) dx = f(b)-f(a)$
That is $int_a^b d/(dx) f(x) dx = f(b)-f(a)$ .

To simplify the statements, take $a=0$
$f(b)-f(0)$

partition the interval into $n$ segments and add each of the segment
$= sum_(i=1)^n (f((b i)/n)-f((b(i-1))/n)$

by mean value theorem, $f((b i)/n)- f((b (i-1))/n)$ $= b/n xx d/(dx) f(x)|_(x=c)$ where $(b i)/n <= c <=(b (i-1))/n$
$= sum_(i=1)^n b/n d/(dx) f(x)$

$h(c) = d/(dx) f(x)|_(x=c)$
$= sum_(i=1)^n h(c) b/n$

applying limit $n->oo$ on both sides, the LHS is a constant so it remains unaffected and not shown
$= lim_(n->oo) sum_(i=1)^n h(c) b/n$

by squeeze value theorem as $n->oo$ , the interval $(b i)/n - (b (i-1))/n = 0$ and so $c =(b i)/n$
$= lim_(n->oo) sum_(i=1)^n h((bi)/n) b/n$

by definition of integral
$= int_0^b h(x)dx$

The above proves $int_a^x d/(dx) f(x) dx = f(x)+c$

in plain Language

The significance of Fundamental Theorem of Calculus:
The relationship between derivative and integral is understood as inverse operations.

Derivative and Integral are inverse operations.

• Derivative of integral of a function is the function.

• Integral of derivative of a function is the function or equivalent.

Summary of what we have learned:

• Differentiation, by the first principles, is the instantaneous-rate-of-change.

• Integration, by the first principles, is the continuous-aggregate.

• Integration is addition of change to an initial value.

• Indefinite integral is defined as a function of variable, where integration is carried out between $0$ and variable $x$ , along with an initial constant.

• Definite integral is defined as the quantity added for an interval $a$ and $b$ . This results in a numerical value.

• First part of fundamental theorem of calculus states that derivative of integral of a function is the function itself.

• Second part of fundamental theorem of calculus states that integral of derivative of a function is the function or an equivalent numerical result.

summary

Fundamental Theorem of Calculus: Given a continuous function $f(x)$ in a closed interval $[a,b]$ and differentiable in open interval $(a,b)$ .
$h(x) = d/(dx) f(x)$
$f(x) = int_a^x g(x)dx$

First part states that $h(x) = g(x)$ ; that is $d/(dx) int_a^x g(x) dx = g(x)$

First part implies that to find $f(x) = int_a^x g(x)dx$ , find the inverse relationship $d/(dx) f(x) = g(x)$ and thus, anti-derivative is defined.

Second part states that $int_a^b h(x) dx = f(b)-f(a)$
That is $int_a^b d/(dx) f(x) dx = f(b)-f(a)$ .

Since the second part is true for any value $x$ in the interval $[a,b]$ , it implies that $int_a^x d/(dx) f(x) dx = f(x) +c$ .

Outline

The outline of material to learn "Integral Calculus" is as follows.

• Detailed outline of Integral Calculus

→ Application Scenario

→ Integration First Principles

→ Graphical Meaning of Integration

→ Definition of Integrals

→ Fundamental Theorem of Calculus

→ Algebra of Integrals

→ Antiderivatives: Standard results

→ Integration of Expressions

→ Integration by Substitution

→ Integration using Identities

→ Integration by Parts

→ Integration by Partial Fraction

→ Integration: Combination of Methods