Integral Calculus : Defining integral in different forms

maths > integral-calculus

Defining integral in different forms

what you'll learn...

Overview

Integrals : Different forms

» Indefinite Integral
    → $\int f (x) d x$ $int f(x)dx$
    → a function of a variable
    → anti-derivative

» Definite Integral
    → $\int_{a}^{b} f (x) d x$ $int_a^b f(x)dx$
    → a numerical value
    → area under the curve between $x = a$ $x=a$ and $x = b$ $x=b$

» Different forms of Summation
    → Riemann Integral
reimann integral     → Darboux Integral
    → Lebesgue Integral

definite and indefinite

Integral of a function $f (x)$ $f(x)$ is specified with an initial value or the constant of integration $c$ $c$ .

Integral of $f (x)$ $f(x)$ with respect to variable $x$ $x$
$quad int f(x) dx =int_0^x f(x)dx + c$

The LHS is referred as indefinite integral.

The integration is taken till a variable $x$ , so the integral is called indefinite.

Contrasting this with "definite integral" : If the integration is taken in a defined interval $[a,b]$ , then, the integral $int_a^b f(x) dx$ is definite integral.

Either of the integration can be loosely referred as "area function".

The word 'definite' means: clearly stated with exact boundaries.

The word 'indefinite' means: of unknown boundary that can change.

definite integral is the continuous aggregate between defined start and end values.

indefinite integral is the continuous aggregate to a variable end value with a constant as initial value.

summary

Definite Integral: For a given function, continuous and integrable in interval $[a,b]$ , the definite integral is $int_a^b f(x) dx$ $= lim_(n->oo) sum_(i=1)^n f(i(b-a)/n) xx (b-a)/n$

Indefinite Integral: For a given function continuous and integrable, the definite integral is $int f(x) dx$ $=c+ lim_(n->oo) sum_(i=1)^n f((ix)/n) xx x/n$

Note: Indefinite integral is also called anti-derivatives. This will be explained in due course.

alternate integrations

Summary of integration: Given $y=f(x)$ a function of variable $x$ , the integral of $y$ is

$int f(x) dx$
$=c+ int_0^x f(x)dx$
$=c+ lim_(n->oo) sum_(i=1)^(n) f((ix)/n)xx x/n$

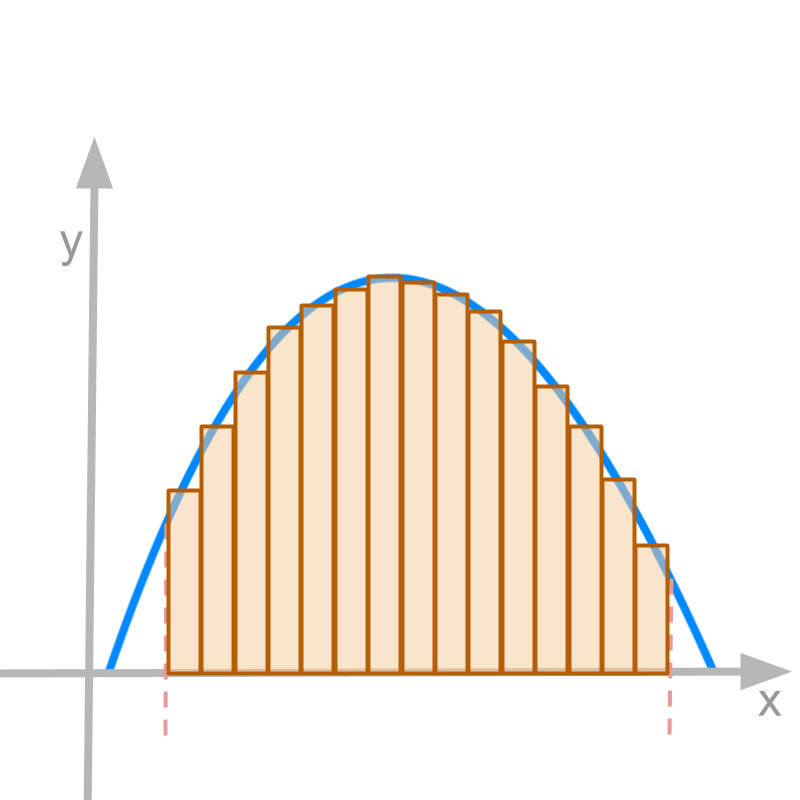
We understood that the summation is given by vertical bars under the curve, as depicted in the figure.

Alternate forms of "limit of summation" are possible, as long as the continuous aggregate is represented.

one alternate

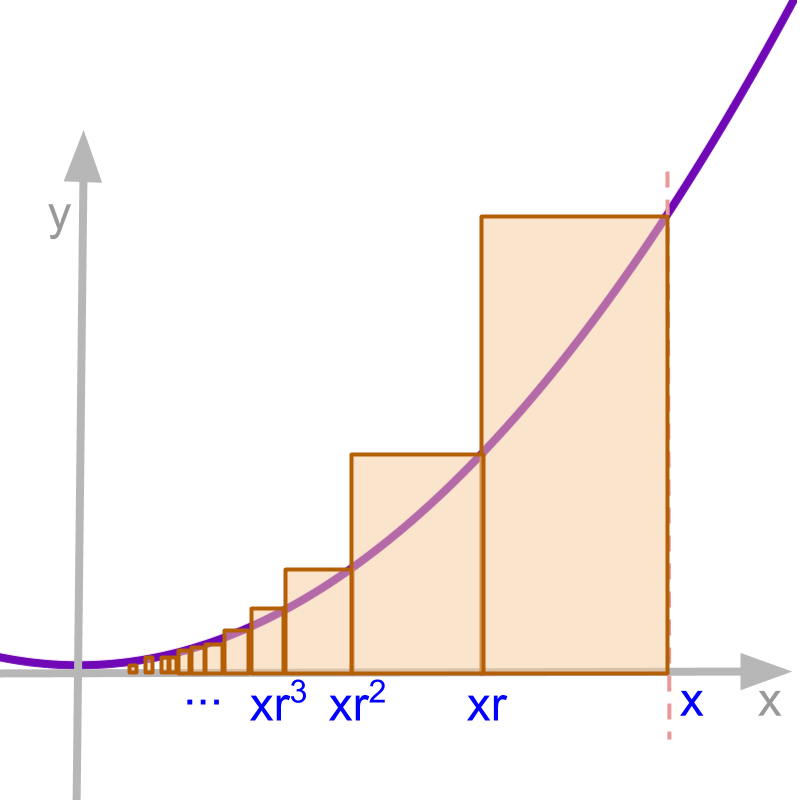
The continuous aggregate is represented under conditions

• the entire interval between $0$ and $x$ is covered

• the width of all partitions (of interval between $0$ and $x$ ) tends to $0$ as $n$ tends to infinity.

An example for an alternate representation is

$int f(x)dx$

$=c + lim_(n->oo) sum_(i=1)^n f(xr^i) xx (xr^i - xr^(i+1))$
where $r<1$

This is represented in the figure. As $n$ tends to infinity, all the partition widths are $0$ and the partition area is identical to the area under the curve.

using the alternate form

Consider $y=x^k$ . The integral represented as

$int f(x)dx$
$=c + lim_(n->oo) sum_(i=1)^n ((i x)/n)^k xx x/n$

There is no simple method to find the limit of this mathematical formulation. So an alternate method is used.

$int f(x)dx$

$=c + lim_(n->oo) sum_(i=1)^n f(xr^i) xx (xr^i - xr^(i+1))$
where $r<1$

In both the representations, as $n$ tends to infinity, all the partition widths are $0$ and the partition area is identical to the area under the curve.

Note: When it was not possible to work-out the limit of the summation, it is about the mathematical formulation of the integral, not the integrability of the function. If the limit of summation is defined, then the function is integrable.

To understand using different forms of summation, let us learn the Fermat's method to calculate the integral of $f(x) = x^k$ .
For simplicity, the constant $c$ is taken to be $0$ , and the integral is between $0$ and $x$ .

$int_0^x f(x)dx$

$=lim_(n->oo) sum_(i=0)^n$ $f(xr^i) xx (xr^i - xr^(i+1))$

$=lim_(n->oo) sum_(i=0)^n$ $x^k r^(ki) xx xr^i(1-r)$

$=lim_(n->oo) sum_(i=0)^n$ $x^(k+1) r^((k+1)i) (1-r)$

$=lim_(n->oo) x^(k+1)$ $(1-r) sum_(i=0)^n r^((k+1)i)$

using geometrical series for sum $sum_(i=0)^(oo) r^((k+1)i)$ $= 1//[(1-r)(1+r+r^2...r^n)]$
$=lim_(n->oo)$ $x^(k+1) (1-r)$ $//[(1-r)(1+r+r^2...r^k)]$

$=lim_(n->oo)$ $x^(k+1)/(1+r+r^2...r^k)$

as limit n tends to $oo$ , the $r$ tends to $1$ .
$=x^(k+1)/(1+1+1...(k+1) text(times))$

$=x^(k+1)/(k+1)$

This proves that $int x^k dx = x^(k+1)/(k+1) + c$

We understood that the continuous aggregate is represented under conditions

• the whole interval between $0$ and $x$ is covered

• the width of all partitions (of interval between $0$ and $x$ ) tends to $0$ as $n$ tends to infinity.

Riemann integral

Definition of Riemann integral is illustrated and explained.
Note: This explains without going into rigorous mathematical formulations.

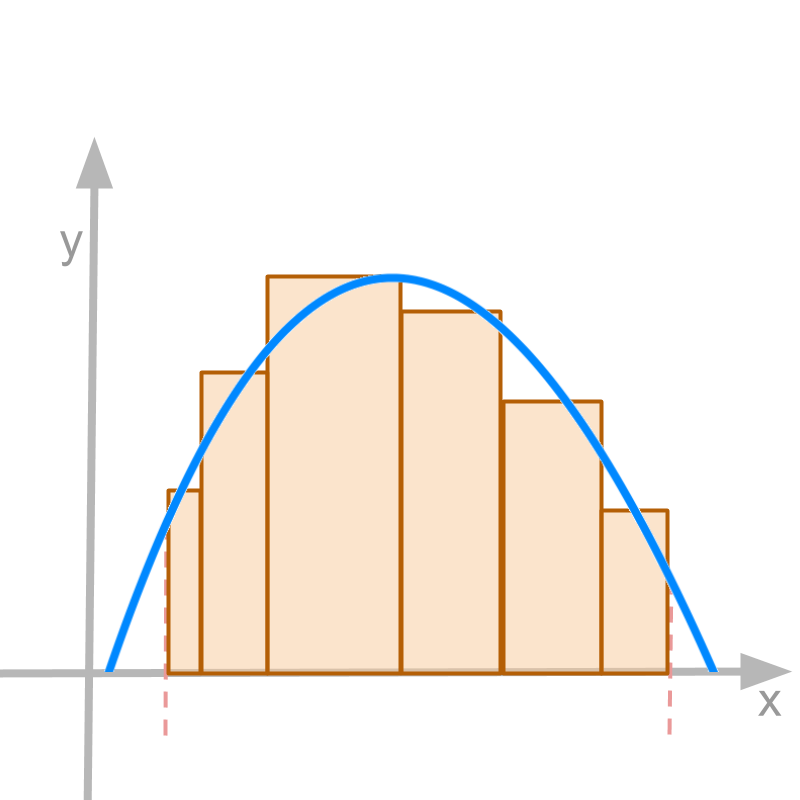
For a given function $f(x)$ continuous and real valued in a closed interval $[a,b]$ , the definite integral $int_a^b f(x)dx$ is illustrated in the figure.

• the partitions can be of different widths

• the partitions span the interval $[a,b]$

• the height of the partitions is any one value of $f(x)$ in that partition width.

• limit on the number of partitions tending to $oo$ and thus the partition widths tends to $0$ .

Under the limit, if the sum is defined, then the function is Riemann integrable in that interval.

When $n$ tends to infinity, This integral is identical to the one defined with partitions of equal widths.

Darboux integral

Definition of Darboux integral is illustrated and explained.
Note: This explains without going into rigorous mathematical formulations

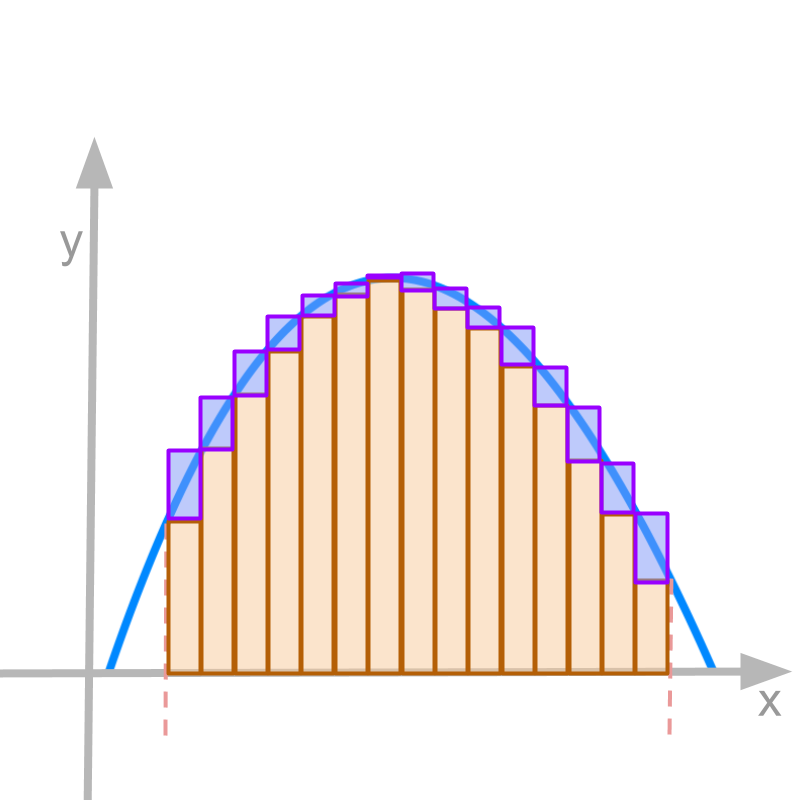
For a given function $f(x)$ continuous and real valued in a closed interval $[a,b]$ , the definite integral $int_a^b f(x)dx$ is illustrated in the figure.

• the partitions can be of unequal widths

• the partitions span the interval $[a,b]$

Two estimates are calculated (1) lower estimate and (2) higher estimate.

• the height of the partitions of lower estimates are the minimum values of $f(x)$ in that partition.

• the height of the partitions of higher estimates are the maximum value of $f(x)$ in that partition.

• limit on the number of partitions tending to $oo$ and thus the partition width tending to $0$ .

• under the limit, if the lower estimate and higher estimate are equal, then the function is Darboux integrable in that interval.

For most integrable functions the results of Darboux integral and Riemann integral are equal.

Lebesgue integral

Definition of Lebesgue integral is illustrated and explained.
Note: This explains without going into rigorous mathematical formulations

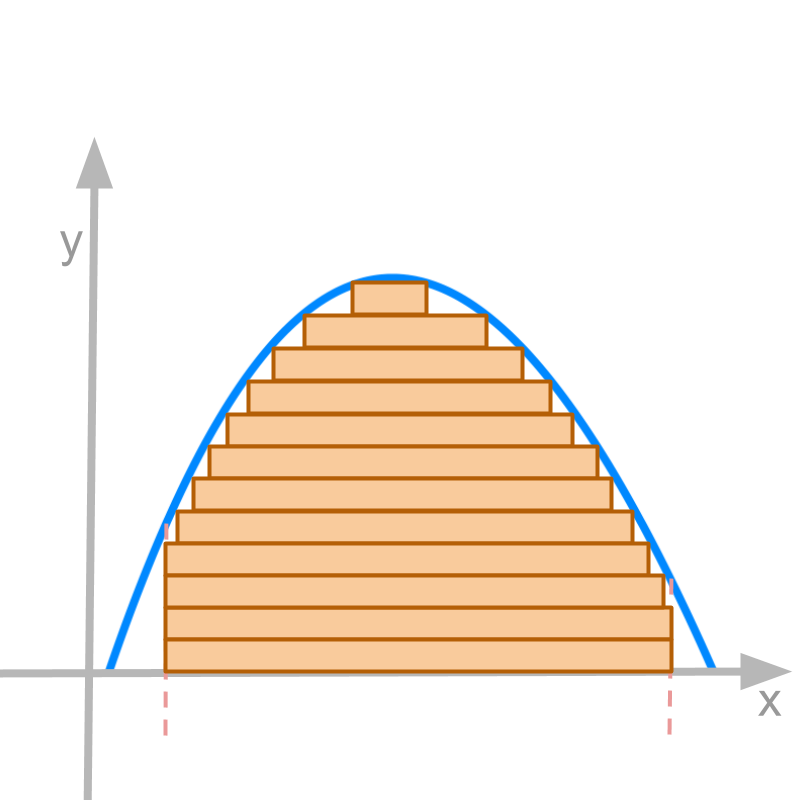
For a given function $f(x)$ continuous and real valued in a closed interval $[a,b]$ , the definite integral $int_a^b f(x)dx$ is illustrated in the figure.

• the partitions are horizontal as illustrated.

• the partitions can be of unequal heights

• the horizontal partitions span the area under the curve

• limit on the number of partitions tending to $oo$ and thus the partition height tends to $0$ .

• Under the limit, if the sum is defined, then the function is Lebesgue integrable in that interval.

The results of Lebesgue integral and Riemann integral are equal for integrable functions.

summary

Outline

The outline of material to learn "Integral Calculus" is as follows.

• Detailed outline of Integral Calculus

→ Application Scenario

→ Integration First Principles

→ Graphical Meaning of Integration

→ Definition of Integrals

→ Fundamental Theorem of Calculus

→ Algebra of Integrals

→ Antiderivatives: Standard results

→ Integration of Expressions

→ Integration by Substitution

→ Integration using Identities

→ Integration by Parts

→ Integration by Partial Fraction

→ Integration: Combination of Methods