Integral Calculus : Understanding Algebra of Integration

maths > integral-calculus

Understanding Algebra of Integration

what you'll learn...

Overview

» Understanding Algebra of Integrals
how integral applies to a function given as algebraic operations of several functions

    → addition and subtraction

    → product and division

    → function-of-function

    → parametric form of function

» Indefinite integrals under Basic Arithmetic Operations
    → $\int a u d x = a \int u d x$ $int audx = a int udx$
    → $\int (u + v) d x = \int u d x + \int v d x$ $int (u+v)dx = int udx + int vdx$
    → $\int (u - v) d x = \int u d x - \int v d x$ $int (u-v)dx = int udx - int vdx$

» Properties of definite integrals

    → $\int_{a}^{b} f (x) d x = \int_{a}^{b} f (y) d y$ $int_a^b f(x) dx = int_a^b f(y) dy$

    → $int_a^a f(x) dx = 0$

    → $int_a^b f(x) dx = -int_b^a f(x)dx$

    → $int_a^b f(x)dx$ $+ int_b^c f(x)dx=$ $int_a^c f(x)dx$

algebra is about operations + - * / ^

What does the title "Algebra of Integration" or "Algebra of Integrals" mean?

The mathematical operations are

• addition and subtraction $u(x) +- v(x)$

• multiple of a function $a u(x)$

• multiplication and division $u(x)v(x)$ and $(u(x))/(v(x))$

• powers and roots $[u(x)]^n$ and $[u(x)]^(1/n)$

• composite form of functions $v (u(x))$

• parametric form of functions $v=f(r) ; u=g(r)$

establishing the problem

Given that $f(x) = u(x)***v(x)$ where $***$ is one of the arithmetic or function operations.

Will there be any relationship between the integrals of the functions $int u(x) dx$ ; $int v(x) dx$ and the integral of the result $int f(x) dx$ ?

Algebra of integration analyses this and provides the required knowledge.

Note: In deriving the results, the functions are assumed to be continuous and integrable at the range of interest. For specific functions at specific intervals, one must check for the continuity and the integrability before using the algebra of integrals.

example problem

For example, consider
$u(x) = x^2$
$v(x) = sin x$
$f(x) = x^2 sin x$

From the standard results, it is known that
$int x^2 dx = x^3/3 + c$ and
$int sin x dx = -cos x + c$ .
What is $int x^2 sin x dx$ ?

In this particular example multiplication is considered. Instead of multiplication, one of the arithmetic or function operations may be considered too.

The algebra of integrals analyses this and provides the required knowledge to solve.

indeginite integral : 3 forms

Indefinite integral or anti-derivative is defined as $int f(x)dx = g(x) +c$ , where $g(x)$ is one of the following

• continuous-aggregate represented by $lim_(n->oo) sum_(i=1)^n f((i x)/n) xx x/n$

• anti-derivative found as $d/(dx) g(x) = f(x)$ .

• the area under the curve $f(x)$ between $0$ and $x$ .

To understand the properties of indefinite integrals one of these is used.

• continuous aggregate provides rigorous mathematical proof.

• anti-derivatives provide proof derived from properties of derivatives.

• area under the curve provide the geometrical methods.

A proof given in one of these three can be verified in other.

scalar multiple

Integral of a scalar multiple of a function: Given $v(x)=color(deepskyblue)au(x)$ .

$int v dx$

$quad quad = lim_(n->oo) sum_(i=1)^n (v((i x)/n) x/n$

$quad quad = lim_(n->oo) sum_(i=1)^n (color(deepskyblue)au((i x)/n) x/n$

with continuity and integrability conditions on $u$
$quad quad = color(deepskyblue)a lim_(n->oo) sum_(i=1)^n (u((i x)/n) x/n$

$quad quad = color(deepskyblue)a int u dx$

The above proves
$int a v dx = a int v dx$ integral of a multiple of a function is multiple of the integral of the function

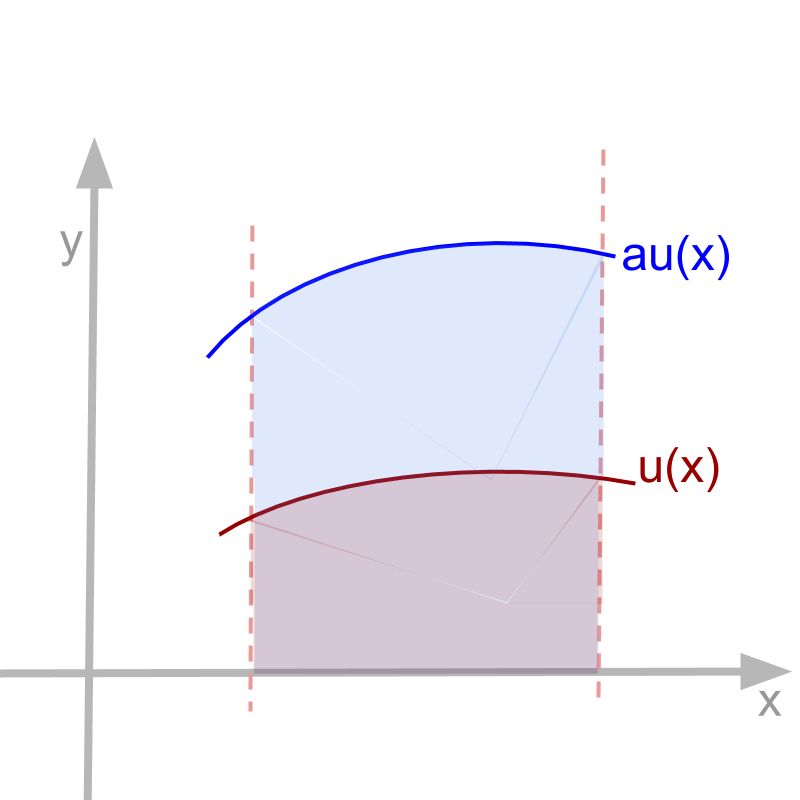
Intuitive understanding for
$int au dx; = a int u dx$

• continuous aggregate multiplies when the function is multiplied by a constant.

• area under the curve multiplies when the $y$ values of curve is multiplied.

Given $int y dx = 2x^2$ and $v=y/5$ , what is $int v dx$ ?

The answer is " $2/5 x^2$ "

$int v dx$
$= int y/5 dx$
$= 1/5 int y dx$
$=1/5 xx 2x^2$
$=2/5 x^2$

sum or difference

Finding integral of sum or difference.

$int (u+v)dx$

$quad = lim_(n->oo) sum_(i=1)^n$ $(u((i x)/n)+-v((i x)/n))$ $xx x/n$

$quad = lim_(n->oo) sum_(i=1)^n$ $u((i x)/n)xx x/n +- v((i x)/n)$ $xx x/n$

with continuity and integrability conditions on $u$ and $v$
$quad = lim_(n->oo) sum_(i=1)^n$ $u((i x)/n)xx x/n$

$+- lim_(n->oo) sum_(i=1)^n$ $v((i x)/n)xx x/n$

$quad quad = int u dx +- int v dx$

The above proves

$int (u+v) dx = int u dx + int v dx$

$int (u-v) dx = int u dx - int v dx$

integral of a sum or difference is the sum or difference of integrals.

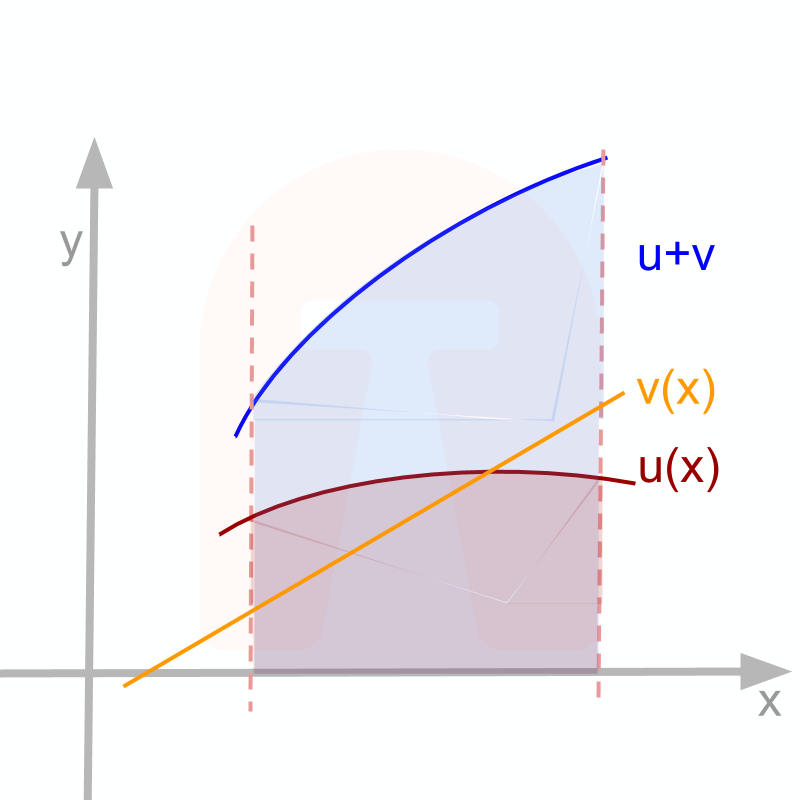
integral of addition or subtraction of functions

Intuitive understanding for
$int (u+-v) dx = int u dx +- int v dx$

• continuous aggregate adds (subtracts) when the function is added(subtracted).

• Areas under the curves add (or subtract) when the functions are added (or subtracted).

Given $int u dx = sinx$ and $int v dx =x+20$ , what is $int (u+v) dx$ ?

The answer is " $sin x + x + 20$ "

summary

Integral of a Multiple:
$int (au)dx = a int u dx$

Integral of Sum or Difference:
$int (u+v) dx = int u dx + int v dx$

$int (u-v) dx = int u dx - int v dx$

Note: Other algebraic operations (like multiplication, function of function, etc.) will be taken up in due course.

Definite integral : 3 forms

Definite integral is defined as $int_a^b f(x)dx = g(b)-g(a)$ , where $g(x)$ is found by either one of the following

• continuous-aggregate represented by $lim_(n->oo) sum_(i=1)^n$ $f(a+(i (b-a))/n) xx (b-a)/n$

• the anti-derivative of $f(x)$ represented by $d/(dx) g(x) = f(x)$ .

• the area under the curve $f(x)$ between $a$ and $b$ .

To understand the properties of definite integrals one of these is used.

• continuous aggregate provides rigorous mathematical proof.

• anti-derivatives provide proof derived from properties of derivatives.

• area under the curve provide the geometrical methods.

A proof given in one of these three can be verified in other.

definite and indefinite

It is noted that anti-derivatives or indefinite integrals can be used to compute definite integrals.

The properties pertaining to addition, subtraction, and multiplication by constant are studied for indefinite integrals. Those are be directly applicable to definite integrals.

change in valriable

Consider two forms of definite integrals.

$int_a^b f(x)dx = g(b)-g(a)$ and $int_a^b f(y)dy = g(b)-g(a)$ .

The left hand side has different variables $x$ and $y$ inside the definite integrals. The right hand side is independent of the variables. The two results of the two integrals are equal?

Intuitive understanding of
$int_a^b f(x) dx = int_a^b f(y) dy$

In $int_a^b f(y)dy$ the variable of integration is $y$ and so the limits $a$ to $b$ are for $y$ .

In $int_a^bf(x)dx$ the variable of integration is $x$ and so the limits $a$ to $b$ are for $x$ .

Despite any relationship between $y$ and $x$ , the given definite integrals are identical.

Given $int_0^2 f(x)dx = 20$ and $y=2x$ , what is $int_0^2 f(y)dy$ ?

The answer is " $20$ ". The change in variable does not change.

zero interval

Given $int_a^b f(x) dx = g(b)-g(a)$ .

This implies $int_a^a f(x)$ $=g(a)-g(a)$ $=0$ .

Intuitive understanding of
$int_a^a f(x) dx = 0$ : The area under the curve is 0 between $a$ and $a$ as the width is $0$ .

traverse the otherway

Given $int_a^b f(x)dx = k$

$int_b^a f(x)dx = -k$

Intuitive understanding of
$int_a^b f(x) dx = -int_b^a f(x)dx$ : The area under the curve is positive when the traversal is in increasing $x$ direction. And the area under the curve is negative when the traversal is in the decreasing $x$ direction. So, when the limits are switched, the direction of traversal reverses.

two ranges

Given $int_a^b f(x)dx = k$ and $int_b^c f(x)dx = l$ , what is $int_a^c f(x)dx$ ? Note: $int_a^b f(x)dx$ is the area under the curve from $a$ to $b$ . $int_b^c f(x)dx$ is the area under the curve from $b$ to $c$ . The question is to find area under the curve from $a$ to $c$ .

$int_a^c f(x)dx$ $=int_a^b f(x)dx$ $+ int_b^c f(x)dx$ .

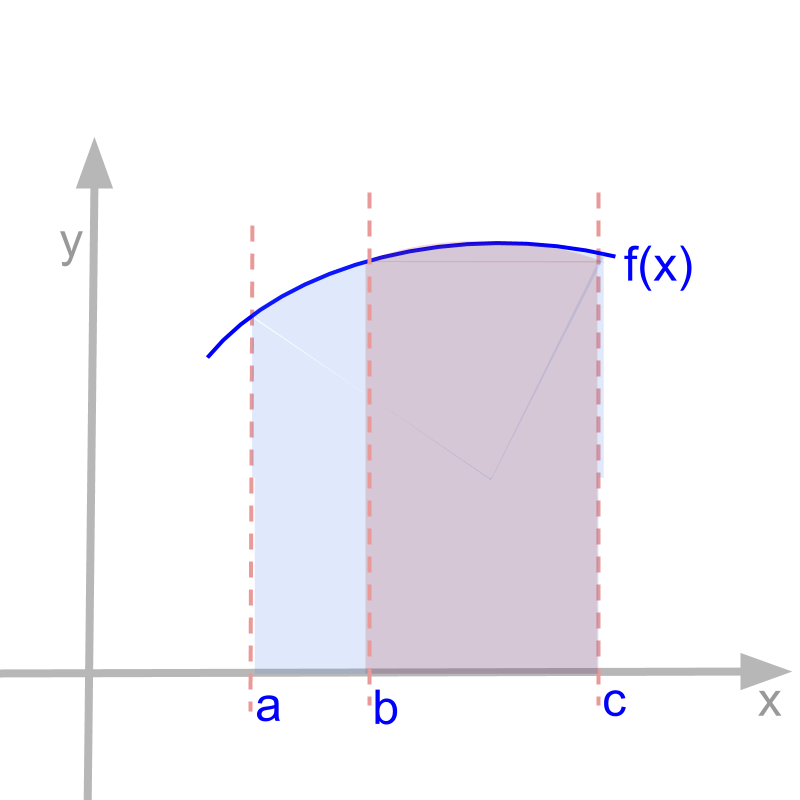
Intuitive understanding of
$int_a^b f(x)dx$ $+ int_b^c f(x)dx=$ $int_a^c f(x)dx$

• the continuous aggregate continues from the end of one integral to the second integral.

Properties of definite integrals is understood as area under the curve

• area under $a$ to $b$ is negative of area under $b$ to $a$

• area under $a$ to $c$ is sum of area under $a$ to $b$ and area under $b$ to $c$

example

Given
$int_a^b f(x) dx = 2$ and $int_c^b f(x) dx = 1$ , what is $int_a^c f(x)dx$ ?

The answer is " $1$ ".

$int_a^c f(x)dx$

$= int_a^b f(x)dx$ $+int_b^c f(x)dx$

$= int_a^b f(x)dx$ $-int_c^b f(x)dx$

$= 2-1$

summary

Properties of Definite Integrals:
$int_a^b f(x) dx = int_a^b f(y) dy$

$int_a^a f(x) dx = 0$

$int_a^b f(x) dx = -int_b^a f(x)dx$

$int_a^b f(x)dx$ $+ int_b^c f(x)dx=$ $int_a^c f(x)dx$

Outline

The outline of material to learn "Integral Calculus" is as follows.

• Detailed outline of Integral Calculus

→ Application Scenario

→ Integration First Principles

→ Graphical Meaning of Integration

→ Definition of Integrals

→ Fundamental Theorem of Calculus

→ Algebra of Integrals

→ Antiderivatives: Standard results

→ Integration of Expressions

→ Integration by Substitution

→ Integration using Identities

→ Integration by Parts

→ Integration by Partial Fraction

→ Integration: Combination of Methods