Mensuration : Length, Area, and Volume

maths

Welcome to the refreshingly new views to calculating perimeter, area, and volume of 2D and 3D shapes.

• Length is Distance-Span, measured in reference span of to $1$ $1$ unit long line

• Area is Surface-Span, measured in reference to span of $1 \times 1$ $1xx1$ square

• Volume is Space-Span, measured in reference to span of $1 \times 1 \times 1$ $1xx1xx1$ cube

In this basic course, the following are covered.

• Perimeter and area of simple 2D shapes

• surface area and volume of simple 3D shapes

maths > mensuration-basics > basicmensu-measuring-standard

Introduction to Standards

This topic introduces the following

• What are standard in measurement?

• What are Absolute Standards?

• What are Derived Standards?

Absolute Standards : An unit of measurement, widely accepted and used in reference to a standardized prototype.

Derived Standards : An unit of measurement that is defined using other absolute standards.

maths > mensuration-basics > basicmensu-measuring-length

Introduction to Measuring Length

This topic introduced measuring length as "distance-span". It is an absolute standard and measured in reference to a standard 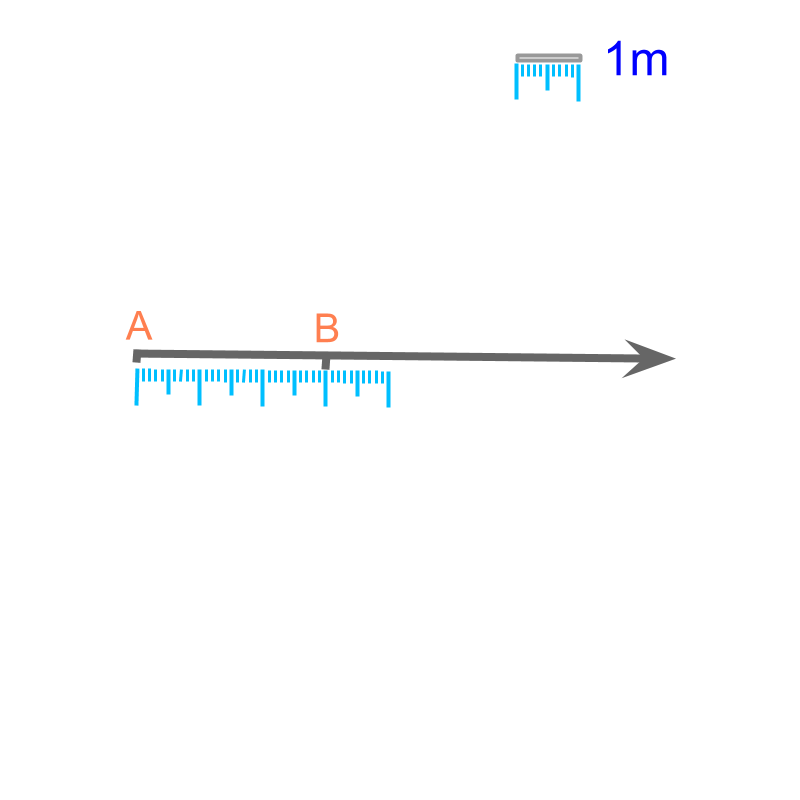$1$ $1$ unit. measurement of length Length : The distance-span between two points is the length. It is measured in meter or in one of its other forms. Length is specified as a number in reference to the reference-prototype-standard meter (or in one of other derived or similar forms).

maths > mensuration-basics > measuring-length-approximation

Accurate measure and Approximate measure

In this topic accuracy of measurement is explained.

Accuracy of Measurements : Measurement can be performed to a desired accuracy level.

When the accuracy is specified to a lower level, the measurement is approximate measurement.

maths > mensuration-basics > basicmensu-measuring-area

Introduction to Measuring Area

This topic introduced measuring area as "surface-span". It is a derived standard and measured in reference to a standard $1 x 1$ $1x1$ square.

Area of a plane figure : The surface-span of a plane figure is the area of the surface. It is measured in square meter (or in one of other derived or similar forms). 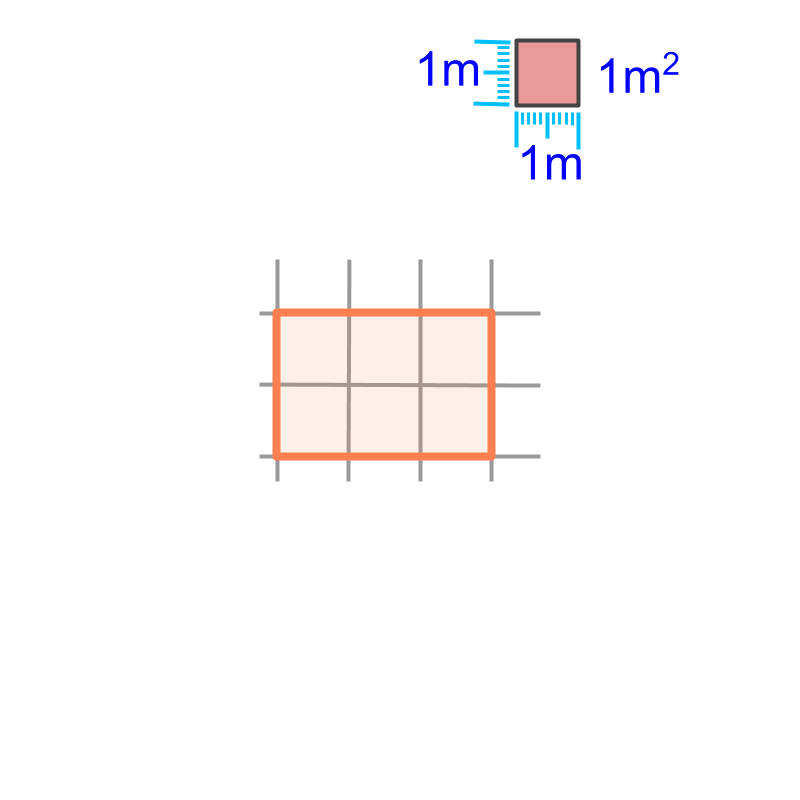measurement of area Area is specified as a number in reference to the surface-span of a square of $1$ $1$ meter side.

maths > mensuration-basics > basicmensu-measuring-volume

Introduction to Measuring Volume

This topic introduced measuring volume as "space-span". It is a derived standard and measured in reference to a standard $1 \times 1 \times 1$ $1xx1xx1$ cube.

Volume of a solid : The space-span of a solid is the volume of the solid. It is measured in cubic meter (or in one of other derived or similar forms.) 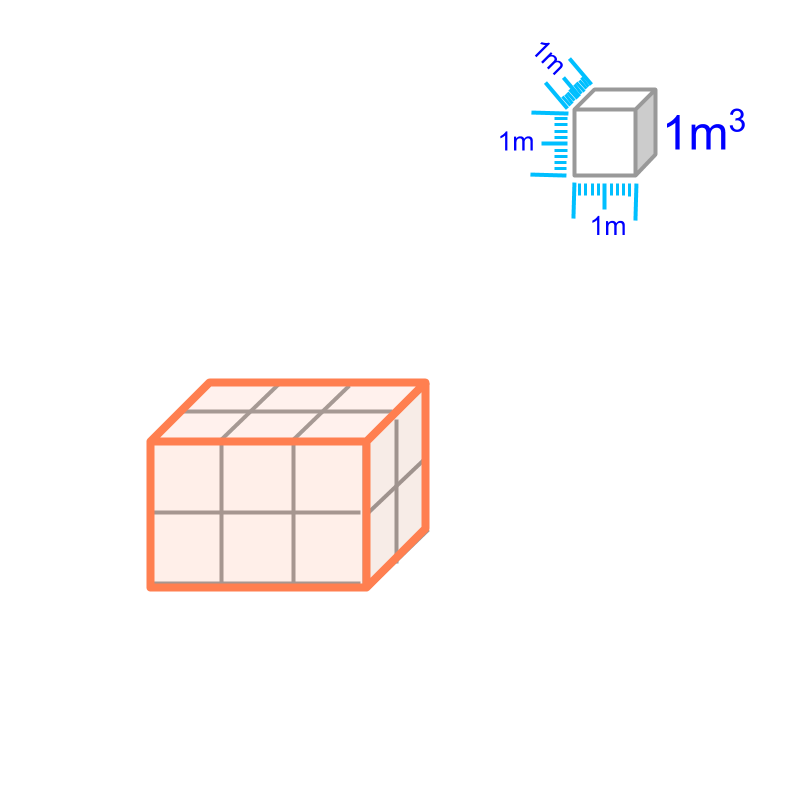measurement of volume Volume is specified as a number in reference to the space-span of a cube of $1$ $1$ meter side.

maths > mensuration-basics > basicmensu-units-conversion

Conversion of Units of Measure

This topic provides a very brief overview of conversion of Units of Measure.

maths > mensuration-basics > basic-perimeter-polygons

Perimeter: Square, Rectangle, Triangle, Polygons

Finding perimeter of simple figures (squares, rectangle, triangle, polygon) are revised.

Perimeter :
Perimeter of a figure is the length of the line or curve forming the boundary of the figure.

Perimeter of square $= 4 \times side$ $=4 xx text( side)$

Perimeter of rectangle $= 2 \times length + width$ $=2 xx text( length + width)$

Perimeter of triangle $= sum of three sides$ $=text( sum of three sides)$

Perimeter of polygon $= sum of sides$ $=text( sum of sides)$

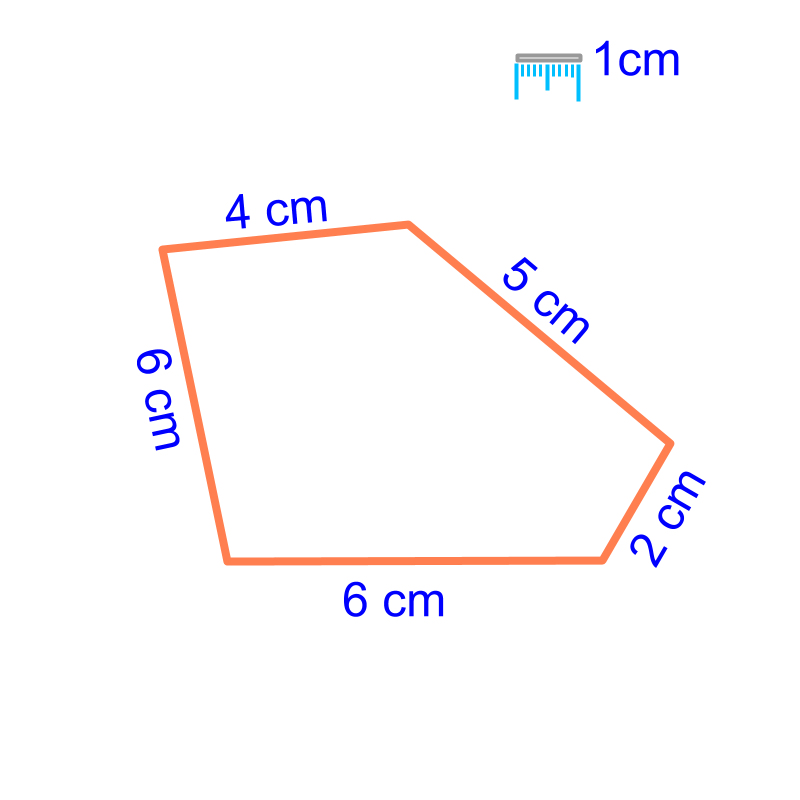
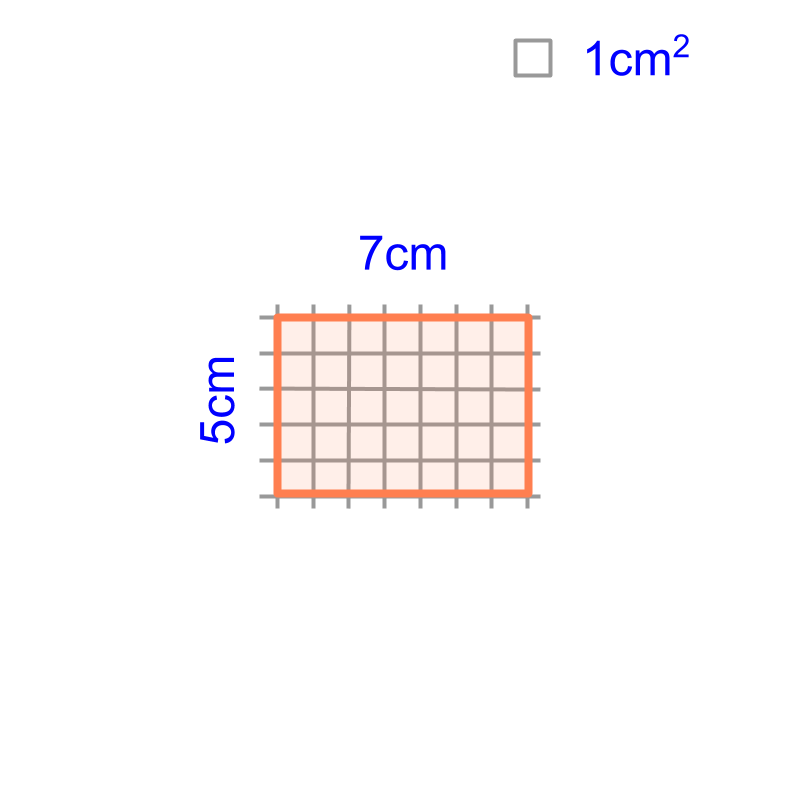
maths > mensuration-basics > basic-area-square-rectangle

Area of Square and Rectangle

Area of a Square and a Rectangle :
Area of square $= {side}^{2}$ $=text( side)^2$

Area of rectangle $= length \times width$ $=text( length ) xx text( width)$

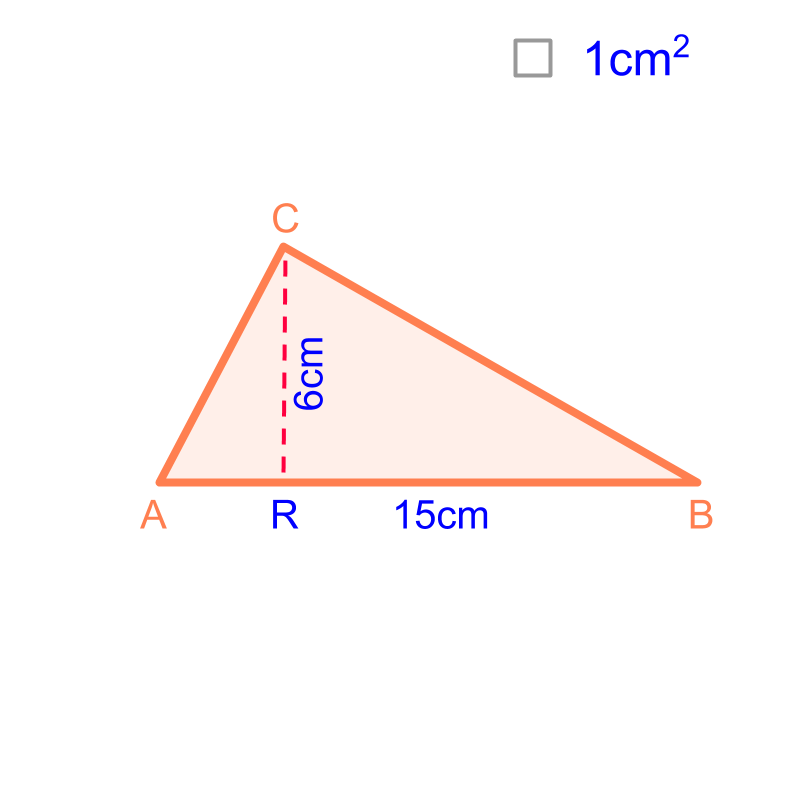
maths > mensuration-basics > basic-area-triangle

Area of a Triangle

The area of a triangle is calculated based on geometrical properties. In this chapter, the different configurations of triangles are illustrated and a common formula is derived.

Area of a Triangle:
$\frac{1}{2} \times base \times (h e i g h t)$ $1/2 xx text( base ) xx ( height)$

maths > mensuration-basics > basic-area-polygons

Area of Polygons

Area of a Polygon : Consider a polygon to be combination of known geometrical forms, mostly triangles.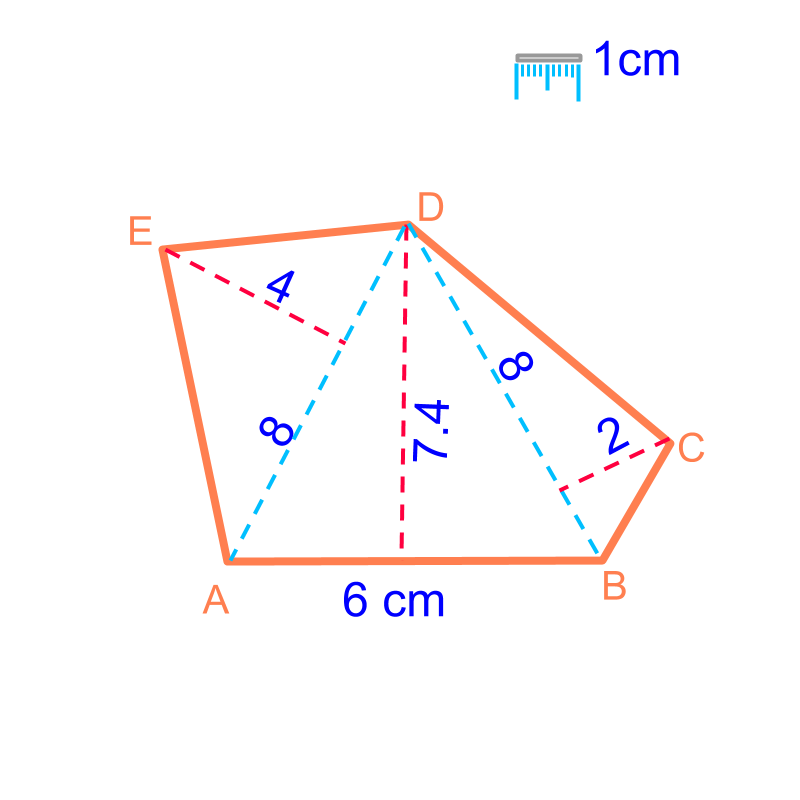 The geometrical forms and the formula for area are:

Area of a triangle $= \frac{1}{2} \times base \times height$ $= 1/2 xx text( base ) xx text( height)$

Area of a trapezium $= \frac{1}{2} \times sum of bases \times height$ $= 1/2 xx text( sum of bases ) xx text( height)$

Area of a parallelogram $= base \times height$ $= text( base ) xx text( height)$

Area of a kite $= \frac{1}{2} \times major-diagonal \times d2$ $= 1/2 xx text( major-diagonal ) xx text( d2)$

maths > mensuration-basics > basic-perimeter-area-circle

Circumference and Area of a Circle

In this page, the formula to find circumference of a circle is introduced.

Circumference of a Circle: :
Circumference $= 2 π r$ $= 2 pi r$ and $= π d$ $=pi d$

$r$ $r$ is the radius of the circle

$d$ $d$ is the diameter of the circle circumference by equivalence Area of a Circle :
$= π r^{2}$ $= pi r^2$

$r$ $r$ is the radius of the circle

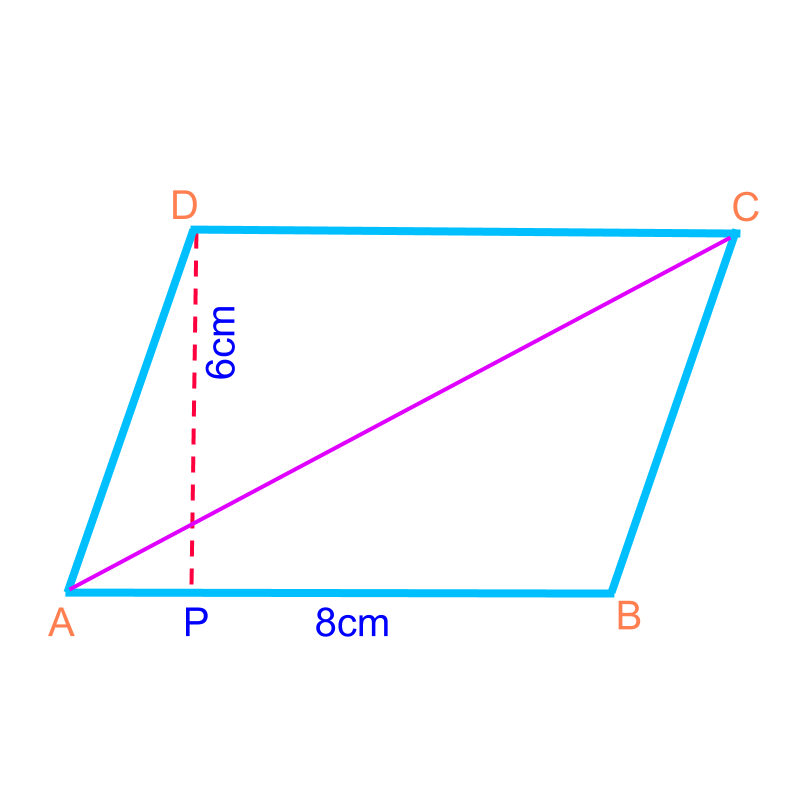
maths > mensuration-basics > basic-mensuration-quadrilaterals

Perimeter and Area of Various Quadrilaterals

In this page, the formula to find area of various quadrilaterals is introduced.

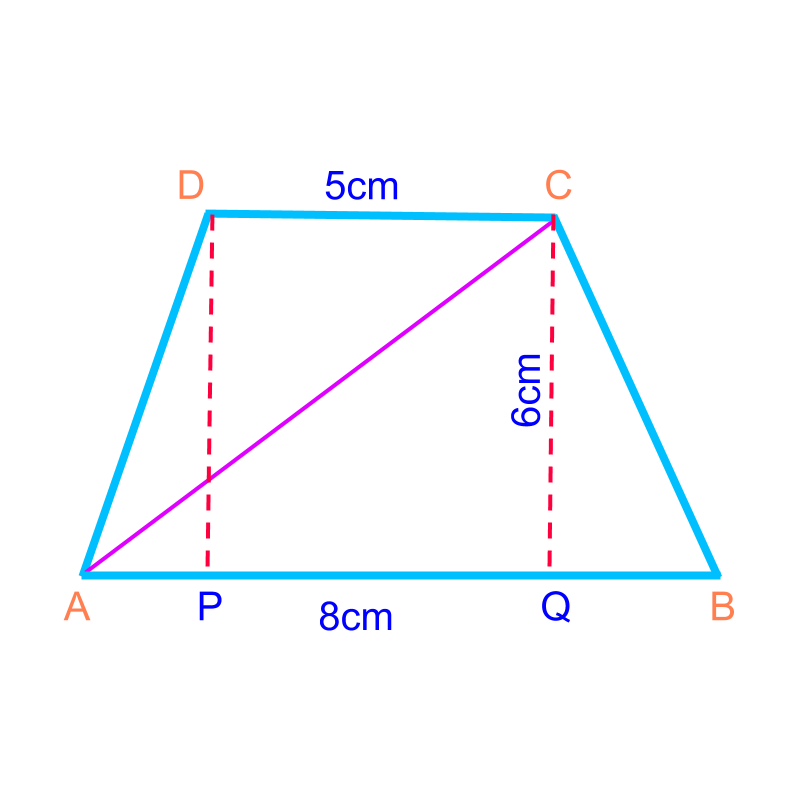
Area of Some Quadrilaterals : Consider the polygon shapes as combination of triangles and find sum of area of the triangles. area of parallelogram $area of a parallelogram$ $text( area of a parallelogram )$ $= base \times height$ $= text( base ) xx text( height)$ area of trapezium $area of a trapezium$ $text( area of a trapezium )$ $= \frac{1}{2} \times sum of bases \times height$ $= 1/2 xx text( sum of bases ) xx text( height)$ area of kite $area of a kite$ $text( area of a kite )$ $= \frac{1}{2} \times product of the diagonals$ $= 1/2 xx text( product of the diagonals)$

maths > mensuration-basics > basic-surface-area-basic-shapes

Surface Area of Cube, Cuboid, Cylinder

In this page, Finding surface area of simple figures (cube, cuboid, and cylinder) are revised without much discussion.

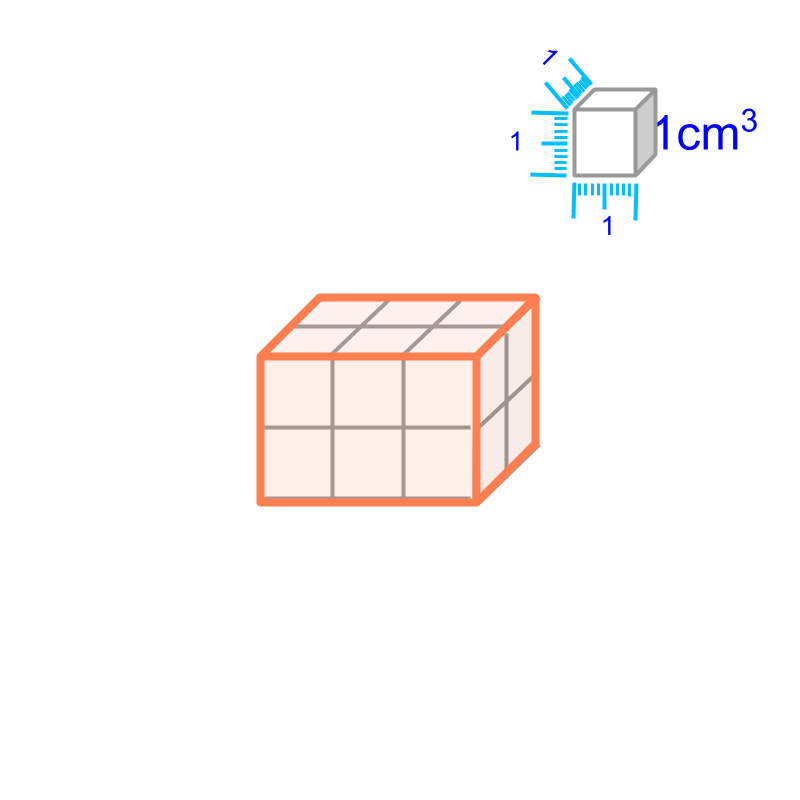Surface Area of Some Shapes: Surface Area of cube $= 6 q^{2}$ $= 6q^2$ Surface Area of cuboid 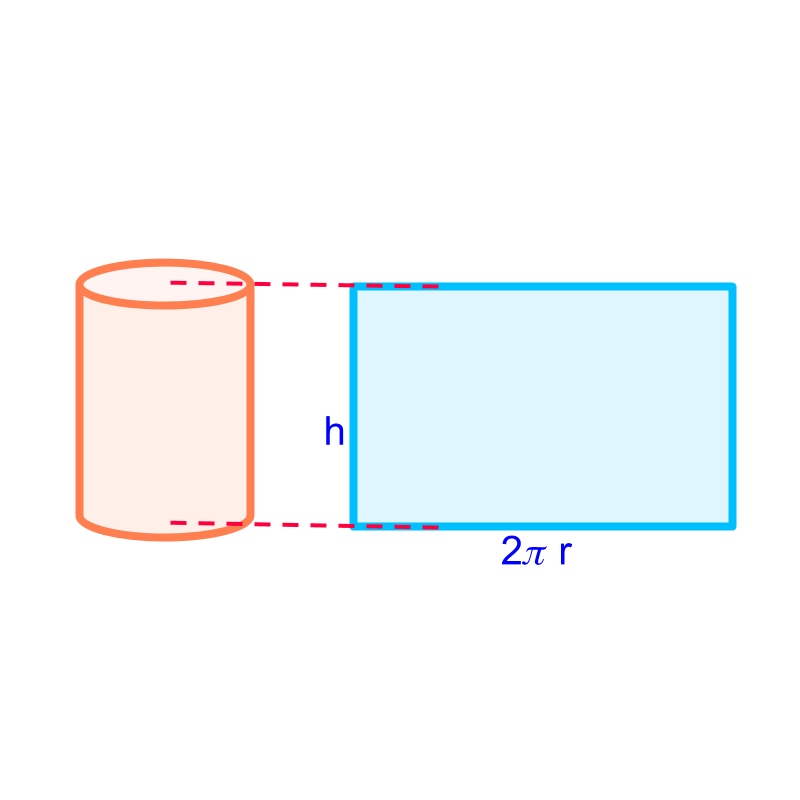$= 2 (l b + b h + h l)$ $= 2(lb+bh+hl)$ Curved Surface Area of Cylinder $= 2 π r h$ $= 2pi r h$

Surface Area of cylinder $= 2 π r (r + h)$ $=2pi r (r+h)$

maths > mensuration-basics > basic-volume-basic-shapes

Volume : Cube, Cuboid, Cylinder

In this page, Finding volume of simple figures (cube, cuboid, and cylinder) are revised without much discussion.

Volume of Some Solids : Volume of cube $= a^{3}$ $= a^3$ Volume of cuboid $= l b h$ $= lbh$ Volume of cylinder $= π r^{2} h$ $= pi r^2 h$