Decimals : Decimals: Not repeating and not ending

maths > decimals

Decimals: Not repeating and not ending

what you'll learn...

overview

On measuring a real-life object, it is found that a number can have decimal digits that do not repeat and do not end. Such decimal numbers -- with decimal digits that do not repeat and do not terminate -- are called "irrational numbers".

numbers in practice

Consider length of a pencil. One of the ways to measure the length of a pencil, is to mark the ends of the pencil into a line-segment and measure the length of the line-segment. This essentially measures the "distance-span between the two ends of the pencil".

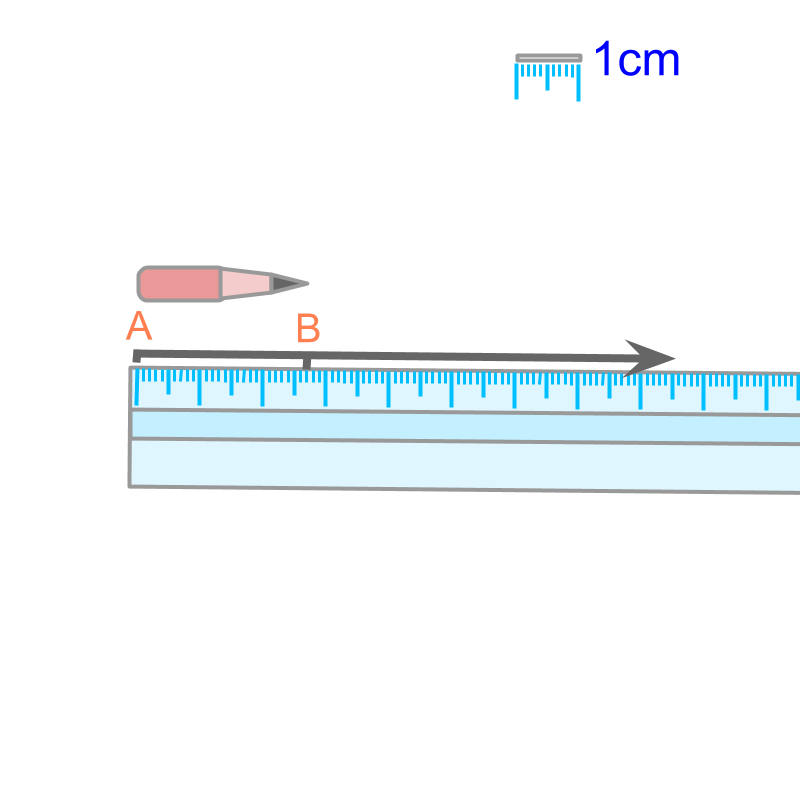
To measure the length of a pencil, an equivalent line segment is taken. The line segment and the graduated scale are shown in the figure. Note the legend on the right-top of the figure showing $1$ $1$ centimeter. What is the length of the line segment $\bar{A B}$ $bar(AB)$ ?

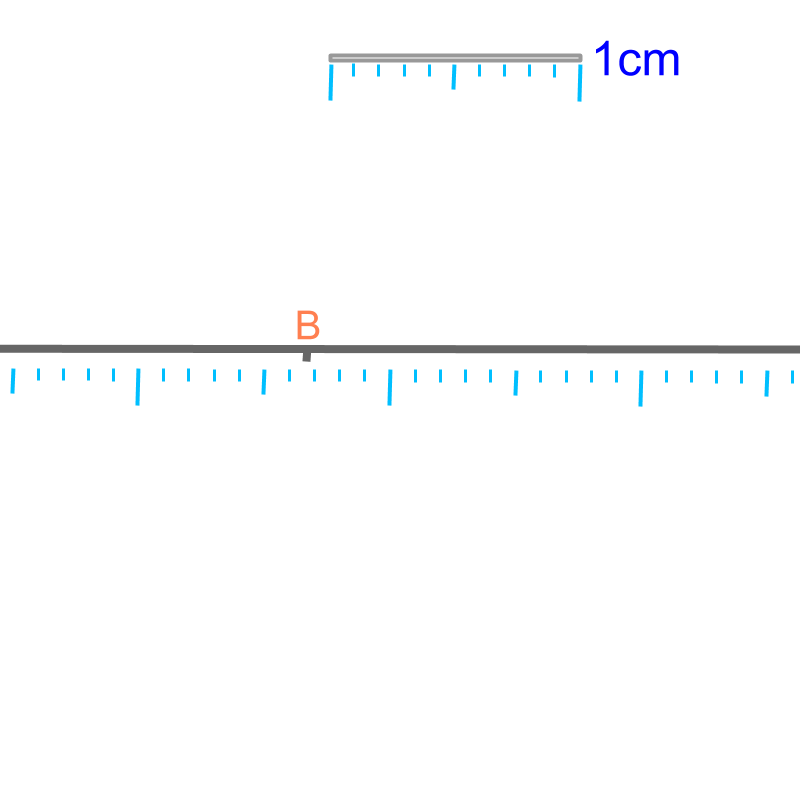
The figure is magnified. Note the legend showing the modified $1 c m$ $1cm$ length. The point $A$ $A$ is not shown. "the length of $\bar{A B}$ $bar(AB)$ is approximately $2.7 c m$ $2.7cm$ "

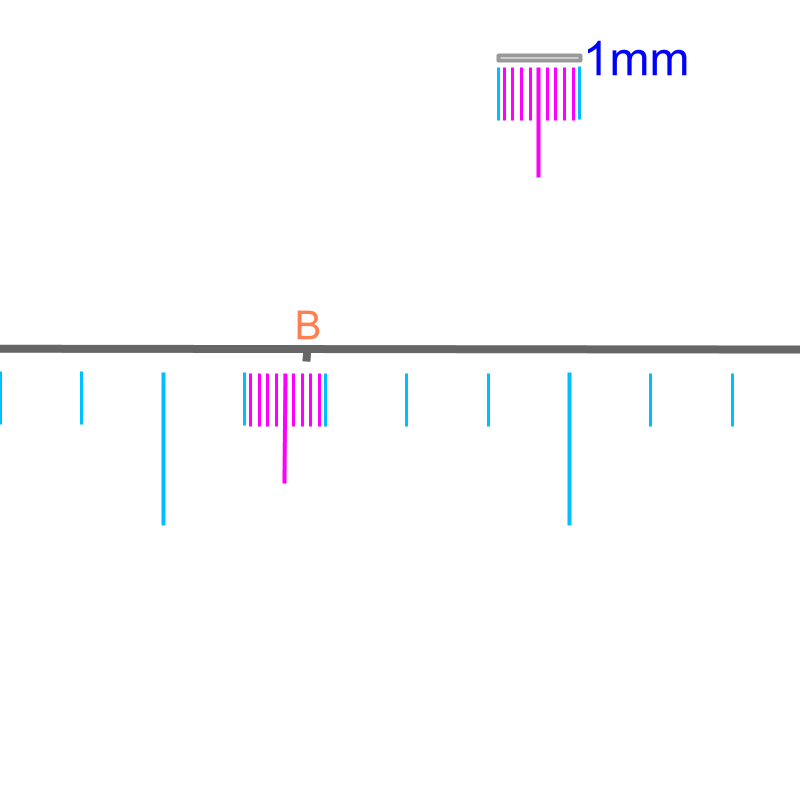
The figure is magnified even larger. Note the legend showing the modified $1 m m$ $1mm$ length. The length of $\bar{A B}$ $bar(AB)$ is better approximated to $2.68 c m$ $2.68cm$

at what accuracy?

The line-segment $\bar{A B}$ $bar(AB)$ can be measured at different accuracies.

• The length is $2.6 c m$ $2.6cm$ when measured with a graduated-scale.

• The length is $2.68 c m$ $2.68cm$ when magnified and measured with a better instrument than a scale.

• The length is $2.68892 \dots$ $2.68892cdots$ when measured at much higher accuracy. For most practical applications, the length of $2.6 c m$ $2.6cm$ is good enough.

Note 1: The line represents a real object. It can be a leaf, or a rod. The important point being, the measurements in real-life are approximated.

Note 2: The length of a real object can be exactly measured too. For example, a pencil of length exactly $2$ $2$ cm is possible. That object, when magnified and measured with high accuracy, will be of length $2$ $2$ cm only.

Note 3: The length of a real object can be a decimal number, that does not end or does not repeat. For example, a pencil is of length $3.68023 \dots$ $3.68023cdots$ cm length. The decimals in the number does not end or repeat. It is an interesting observation, that will help to understand some concepts later.

The word "accuracy" means: state of being exactly correct.

defining

The word "irrational" means: that cannot be given as a ratio.

Irrational Numbers : Decimal numbers that has decimal digits that do not end and do not have a pattern of digits that repeats. eg: accurate length of a pencil is $2.68892 \dots$ $2.68892cdots$ .

advanced concepts

advanced concepts (not for regular readers)

There are two types of decimal numbers with decimal digits that do not end and do not have a pattern that repeats.

• Algebraic irrational numbers: Irrational numbers that are solutions to algebraic equations. eg: The square root of $2$ $2$ which is a solution to $x^{2} = 2$ $x^2=2$ .

• Transcendental irrational numbers: Numbers that are not solutions to algebraic equations. The ratio of circumference to diameter of a circle is an irrational numbers. The diameter is chosen to be in the given standard $1$ $1$ cm. Circle is a regular curve and the length of the curve is measured accurately and found to be an irrational number.

In transcendental irrational numbers, the following is included.
Accurate measurement of real-life object in a unrelated standard.

eg: $1$ $1$ pound is approximated to $453.5924277$ $453.5924277$ grams. Pound is a standard defined based on mass of $7000$ $7000$ grains (wheat or barley). Kilogram is a standard defined based on mass of $1$ $1$ liter water at the temperature of melting point. This irrational number is similar to the example illustrated above -- accurately measuring a real-life object.

Similarly, curve-length of a circle is a measurement in an unrelated standard and so is a irrational number.

summary

Irrational Numbers : Decimal numbers that has decimal digits that do not end and do not have a pattern of digits that repeats. eg: accurate length of a pencil is $2.68892 \dots$ $2.68892cdots$ .

Outline

The outline of material to learn "decimals" is as follows.

Note: goto detailed outline of Decimals

• Decimals - Introduction

→ Decimals as Standard form of Fractions

→ Expanded form of Decimals

• Decimals - Conversion

→ Conversion between decimals and fractions

→ Repeating decimals

→ Irrational Numbers

• Decimals - Arithmetics

→ Comparing decimals

→ Addition & Subtraction

→ Multiplication

→ Division

• Decimals - Expressions

→ Expression Simplification

→ PEMA / BOMA