Decimals : Decimal Addition and Subtraction

maths > decimals

Decimal Addition and Subtraction

what you'll learn...

overview

Addition or Subtraction of decimals is explained. The following are explained for decimals.

• addition in first principles -- combining two quantities and measuring the combined

• subtraction in first principles -- taking away a part of a quantity and measuring the remaining quantity.

• Simplified procedure : Sign property of Addition and Addition by place value

• Simplified procedure : Sign property of Subtraction and Subtraction by place value

combine

Addition represents "putting-together" or "combining" of two quantities.

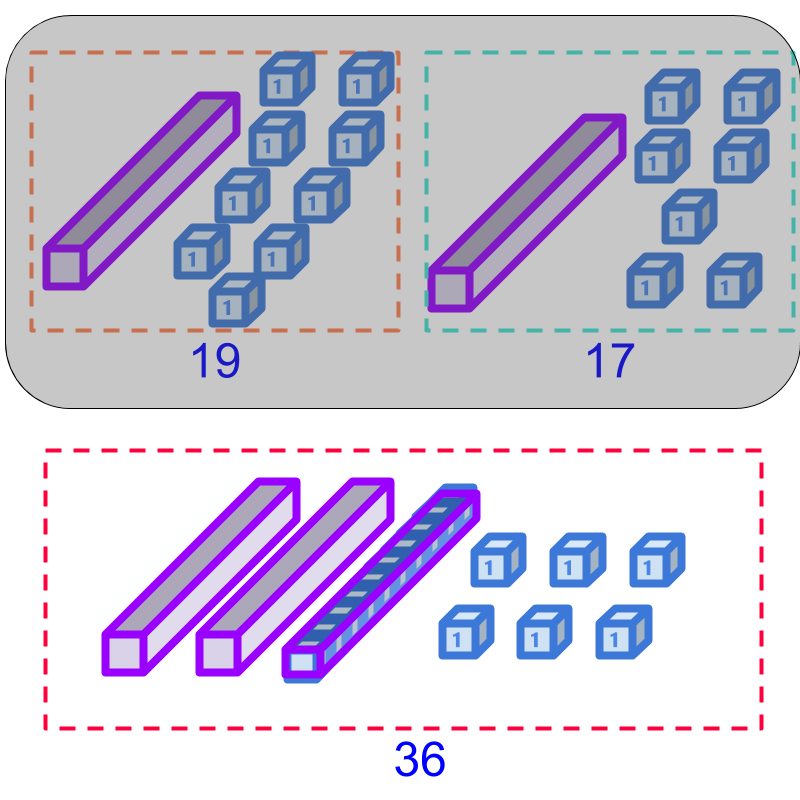
In whole numbers addition, We learned "regrouping" or "carry-over" -- " $10$ $10$ of a lower place-value can be grouped into $1$ $1$ of immediate higher place-value".

Addition of $19$ $19$ and $17$ $17$ is illustrated in the figure.

Addition of $19$ $19$ and $17$ $17$ is sum of $1$ $1$ ten, $9$ $9$ units, and $1$ $1$ ten $7$ $7$ units. This equals $2$ $2$ tens and $16$ $16$ units. $10$ $10$ units is regrouped into $1$ $1$ ten, making the sum as $2 + 1 = 3$ $2+1=3$ tens and $6$ $6$ units. In whole number form, it is $36$ $36$ .

In integer addition, we studied "sign-property of addition" -- "the positive and negative sign of the numbers are handled when adding the numbers".

take away

Subtraction represents "taking-away" or "removing" a number of quantities from another number.

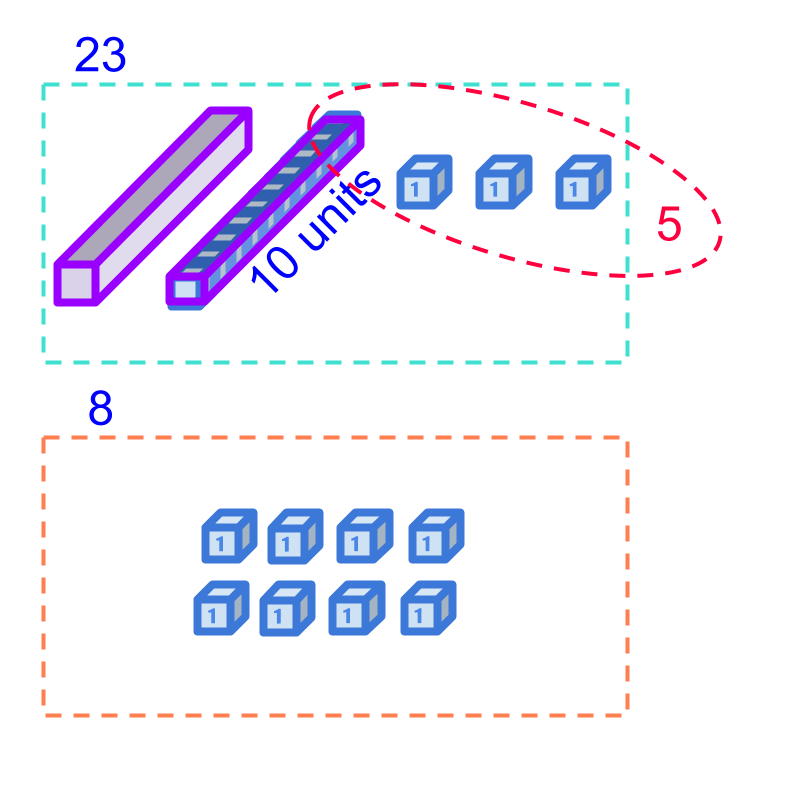
In whole numbers subtraction, we studied "de-grouping" or "borrowing" - " $1$ $1$ of a higher place-value can be split into $10$ $10$ of immediate lower place-value

Subtraction of $15$ $15$ from $23$ $23$ is illustrated in the figure.

Subtraction $23 - 15$ $23-15$ is taking away of $1$ $1$ ten, $5$ $5$ units, from $2$ $2$ tens $3$ $3$ units. To achieve that, $1$ $1$ ten (from minuend $2$ $2$ tens $3$ $3$ units) is de-grouped to $10$ $10$ units and added to the $3$ $3$ units. From the $13$ $13$ units, $5$ $5$ is taken away. The result is $8$ $8$ units.

In integer subtraction, "subtraction is handled as inverse of addition".

For example, to subtract $2$ $2$ from $- 5$ $-5$ , the subtraction is modified into addition $(- 5) - (2) = (- 5) + (- 2)$ $(-5)-(2) =(-5)+(-2)$ . The rules of addition are followed in this.

$aligned: 2$ $text(aligned:)2$ in integer form " $2$ $2$ ". It is also given as $received: 2$ $text(received:)2$ .

$opposed: 2$ $text(opposed:)2$ in integer form is " $- 2$ $-2$ ". It is also given as $given: 2$ $text(given:)2$ .

Directed numbers, positive and negative, are explained as "aligned in direction" and "opposed in direction".

addition (recap)

In whole-numbers, integers, and fractions, we have learned addition of numbers.

Addition First Principles : Two numbers representing count or measurement are put-together and the combined quantity is counted or measured.

Addition by Place-Value with regrouping: The digits of corresponding place-value positions are aligned and added. At each place-value position, the sum is regrouped. This is called carry-over.

Sign-property of Addition : The signs of the addends are handled appropriately
• positive + positive is simple addition
• positive + negative is subtraction of the number with smaller absolute value from the number with larger absolute value. The sign of the sum is the sign of the larger absolute value.
• negative + negative is simple addition with negative as the sign of the sum.

subtraction (recap)

In whole-numbers, integers, and fractions, we have learned subtraction.

Subtraction First Principles : A number representing count or quantity is taken-away from another number and the remaining quantity is counted or measured.

Subtraction by Place-Value with de-grouping: The digits of corresponding place-value positions are aligned and subtracted. At each place-value position, the minuend is de-grouped if subtrahend is larger. This is called borrowing.

Subtraction of Integers : The subtraction is converted to addition of minuend and negative of subtrahend. The sign-property of addition is applicable.

Let us see the decimal addition and subtraction now.

simple examples

The sum of $0.2$ $0.2$ and $0.3$ $0.3$ is " $0.5$ $0.5$ ".

$0.2$ $0.2$ represents $2$ $2$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece.
$0.3$ $0.3$ represents $3$ $3$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece.

Addition is combining the quantities and counting or measuring together.

Together, the quantities make $5$ $5$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece, equaling $0.5$ $0.5$ in decimal.

The difference $0.3 - 0.2$ $0.3-0.2$ is " $0.1$ $0.1$ ".

$0.3$ $0.3$ represents $3$ $3$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece.
$0.2$ $0.2$ represents $2$ $2$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece.

Subtraction is taking-away an amount from another and counting or measuring the remaining.

The remaining makes $1$ $1$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece, equaling $0.1$ $0.1$ in decimal.

carry over in decimals

The sum of $0.19$ $0.19$ and $0.17$ $0.17$ is " $0.36$ $0.36$ ".

$0.19$ $0.19$ represents $1$ $1$ count of $1 / 10^{t h}$ $1//10^(th)$ piece and $9$ $9$ counts of $1 / 100^{t h}$ $1//100^(th)$ piece.
$0.17$ $0.17$ represents $1$ $1$ count of $1 / 10^{t h}$ $1//10^(th)$ piece and $7$ $7$ counts of $1 / 100^{t h}$ $1//100^(th)$ piece.
Addition is combining the quantities and counting or measuring together.

Together, the quantities make $2$ $2$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece and $16$ $16$ counts of $1 / 100^{t h}$ $1//100^(th)$ pieces. $10$ $10$ counts of $1 / 100^{t h}$ $1//100^(th)$ pieces can be regrouped to $1$ $1$ count of $1 / 10^{t h}$ $1//10^(th)$ pieces. This together makes, $2 + 1 = 3$ $2+1=3$ counts of $1 / 10^{t h}$ $1//10^(th)$ pieces and $6$ $6$ counts of $1 / 100^{t h}$ $1//100^(th)$ pieces, equaling $0.36$ $0.36$ in decimal.

taking away in decimals

The difference $0.36 - 0.17$ $0.36-0.17$ is " $0.19$ $0.19$ ".

Subtraction is taking-away an amount from another and counting or measuring the remaining.

In the $1 / 100^{t h}$ $1//100^(th)$ place, $7$ $7$ counts subtrahend is subtracted from $6$ $6$ counts minuend. Since minuend is smaller, $1$ $1$ count from immediate higher place value is de-grouped or borrowed to make minuend at $1 / 100^{t h}$ $1//100^(th)$ place $16$ $16$ and at $1 / 10^{t h}$ $1//10^(th)$ place $2$ $2$ .

Subtracting $7$ $7$ counts from $13$ $13$ counts, the different is $9$ $9$ counts in $1 / 100^{t h}$ $1//100^(th)$ place.

Subtracting $1$ $1$ count from $2$ $2$ counts, the difference is $1$ $1$ count in $1 / 10^{t h}$ $1//10^(th)$ place.

These two makes the difference as $1$ $1$ count in $1 / 10^{t h}$ $1//10^(th)$ place and $9$ $9$ counts in $1 / 100^{t h}$ $1//100^(th)$ place, equaling $0.19$ $0.19$ in decimal.

aligning place value in decimals

The sum of $1.2$ $1.2$ and $0.3$ $0.3$ is " $1.5$ $1.5$ ".

$1.2$ $1.2$ represents $1$ $1$ count of whole and $2$ $2$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece.
$0.3$ $0.3$ represents $3$ $3$ count of $1 / 10^{t h}$ $1//10^(th)$ piece.

Together, the quantities make $1$ $1$ count of whole and $5$ $5$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece, equaling $1.5$ $1.5$ in decimal.

The difference of $1.2 - 0.3$ $1.2 - 0.3$ is " $0.9$ $0.9$ ".

The numbers are aligned at the corresponding place-value positions. By de-grouping or borrowing, the $1 / 10^{t h}$ $1//10^(th)$ place of minuend is $12$ $12$ counts. Subtracting $3$ $3$ counts from that, the difference is $9$ $9$ counts of $1 / 10^{t h}$ $1//10^(th)$ piece, equaling $0.9$ $0.9$ in decimal.

directed decimals

The sum of $0.5$ $0.5$ and $- 0.3$ $-0.3$ is " $0.2$ $0.2$ ".

Note that, positive and negative numbers are "aligned" and "opposed" directions in directed numbers.

$0.5$ $0.5$ represents $5$ $5$ aligned counts of $1 / 10^{t h}$ $1//10^(th)$ piece.
$- 0.3$ $-0.3$ represents $3$ $3$ opposed counts of $1 / 10^{t h}$ $1//10^(th)$ piece.

Addition is combining the quantities and counting or measuring together. $5$ $5$ aligned and $3$ $3$ opposed make together is $2$ $2$ aligned.

Together, the quantities make $2$ $2$ aligned counts of $1 / 10^{t h}$ $1//10^(th)$ piece, equaling $0.2$ $0.2$ in decimal.

The sum of $- 0.5 - 0.3$ $-0.5-0.3$ is " $- 0.8$ $-0.8$ ".

Note that, positive and negative numbers are "aligned" and "opposed" directions in directed numbers.

$- 0.5$ $-0.5$ represents $5$ $5$ opposed counts of $1 / 10^{t h}$ $1//10^(th)$ piece.
$0.3$ $0.3$ represents $3$ $3$ aligned counts of $1 / 10^{t h}$ $1//10^(th)$ piece.

When handling directed numbers, Subtraction is handled as inverse of addition (explained in integers).

$- 0.5 - 0.3$ $-0.5-0.3$
$= (- 0.5) + (- 0.3)$ $=(-0.5) + (-0.3)$
Follow the decimal addition procedure.

Together, the quantities make $8$ $8$ opposed counts of $1 / 10^{t h}$ $1//10^(th)$ piece, equaling $- 0.8$ $-0.8$ in decimal.

decimal addition & subtraction

Decimal Addition - First Principles : The numbers representing quantities are combined together and the combined quantity is measured or counted.

Decimal Subtraction - First Principles : The subtraction is handled as addition of minuend and negative of subtrahend.

In decimal addition, the following are understood.

• handling the sign (positive or negative)

• adding at place-value of the digits

• the regrouping at digit level.

Let us look at the simplified procedure to add or subtract decimals.

addition by place-value

In whole numbers, we studied addition as combining two quantities. the simplified procedure for whole number addition is "Addition by place-value with regrouping".

An example is illustrated in the figure. $156 + 88 = 244$ $156+88 = 244$

subtraction by place-value

In whole numbers, we studied subtraction as removing an amount from a quantity. The simplified procedure for whole number subtraction is "Subtraction by place-value with de-grouping".

An example is illustrated in the figure. $156 - 88 = 68$ $156 - 88 = 68$ .

sign property of addition

In integers, we studied about addition of directed whole-numbers (that is, numbers with signs). The simplified procedure for integer addition is "sign-property of integer addition".

The sign-property of integer addition is given as

• positive + positive is whole number addition

• positive + negative is subtraction of the number with smaller absolute value from the other. The difference is the absolute value of the result. The sign of result is the sign of the number with larger absolute value.

• negative + negative is the sum of absolute values with negative sign.

This was explained in integers.

subtraction as inverse of addition

In integers, we studied about subtraction of directed whole-numbers (that is, numbers with signs). The simplified procedure for integer subtraction is "convert the subtraction to inverse of addition and then, add based on sign-property of integer addition".

$- 5 - 3 = - 5 + (- 3) = - 8$ $-5 - 3 = -5 + (-3) = -8$ .

place-value order

The extended place value order for decimals is " $\dots <$ $cdots <$ hundredth $<$ $<$ tenth $<$ $<$ units $<$ $<$ tens $<$ $<$ hundreds $< \dots$ $< cdots$ ".

simplify decimal addition

The sum of $2.14 + 1.32$ $2.14 + 1.32$ is " $3.46$ $3.46$ ". By first principles, the values are combined and the combined quantity is counted.

A simplified procedure is designed to represent the addition by first principles.

The digits of the numbers are aligned by place-value. The digits are added in place-value.

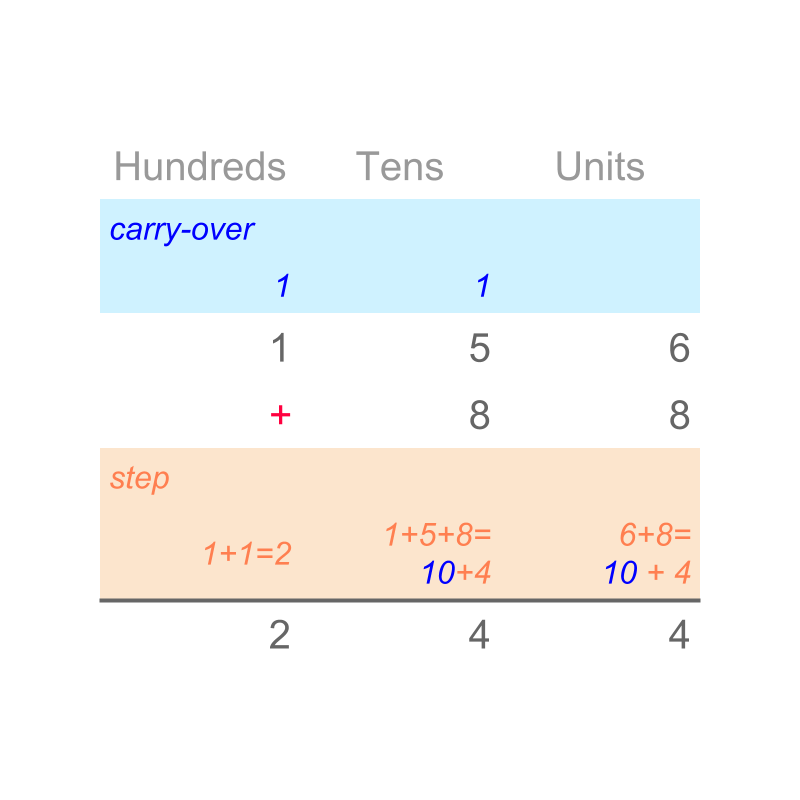
The sum of $2.14 + 1.32 = 3.46$ $2.14 + 1.32 = 3.46$

What is the sum of $1.56 + 0.88$ $1.56 + 0.88$ ?
The answer is " $2.44$ $2.44$ ". By first principles, the values are combined and the combined quantity is counted. When a sum at a place value is greater than or equal to $10$ $10$ , it is regrouped to the immediate higher place-value.

A simplified procedure is designed to represent the addition by first principles.

Consider the addition of $1.56 + 0.88$ $1.56 + 0.88$ . The digits of the numbers are aligned by place-value. Note that $5$ $5$ of tenth place-value is aligned to $8$ $8$ of tenth place value. The digits are added in place-value starting from the lowest place-value hundredth. The result $6 + 8 = 14$ $6+8=14$ is regrouped to $1$ $1$ tenth and $4$ $4$ hundredths. This is repeated.

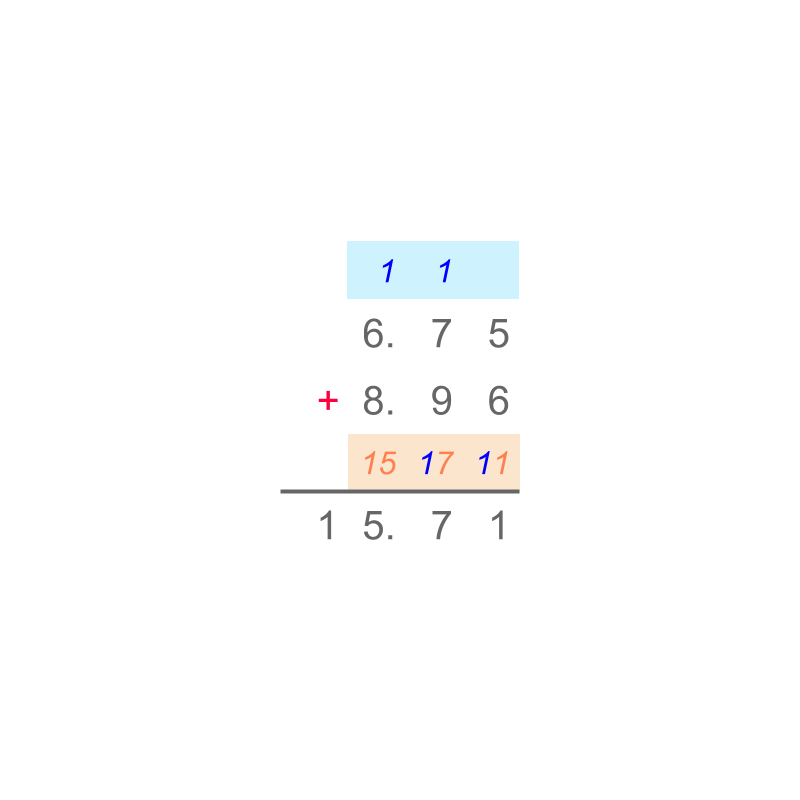
The sum of $6.75 + 8.96$ $6.75 + 8.96$ is " $15.71$ $15.71$ ". The simplified procedure is given in figure.

simplify decimal subtraction

The difference $2.74 - 1.32$ $2.74 - 1.32$ is " $1.42$ $1.42$ ".

By first principles, the subtrahend amount is taken-away from minuend and remaining is counted.

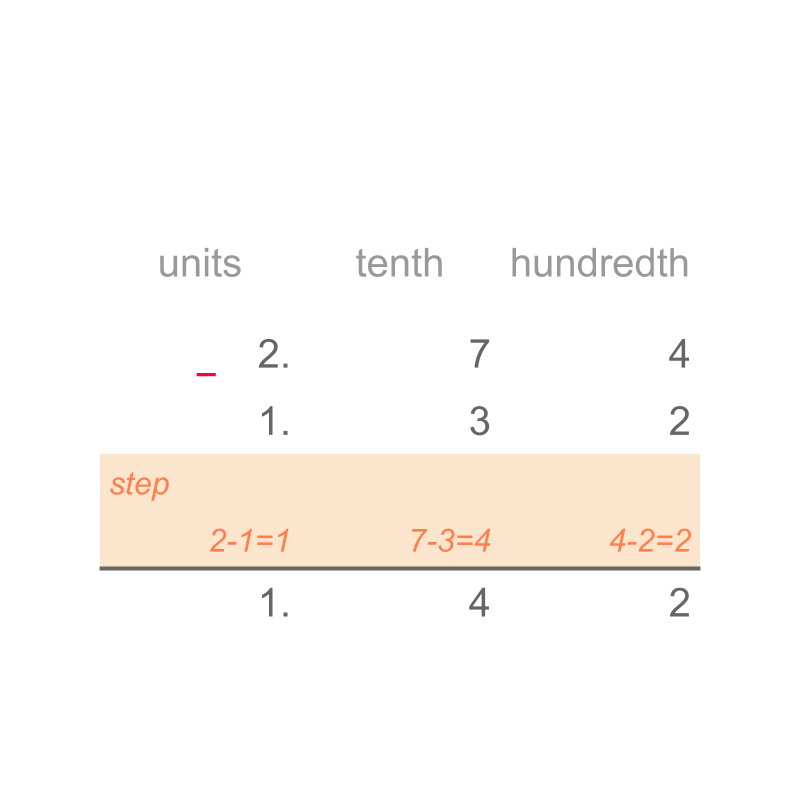
A simplified procedure is designed to represent the subtraction by first principles.

Consider the subtraction $2.14 - 1.32$ $2.14 - 1.32$ . The digits of the numbers are aligned by place-value. The digits are subtracted in place-value. The simplified procedure is given in figure.

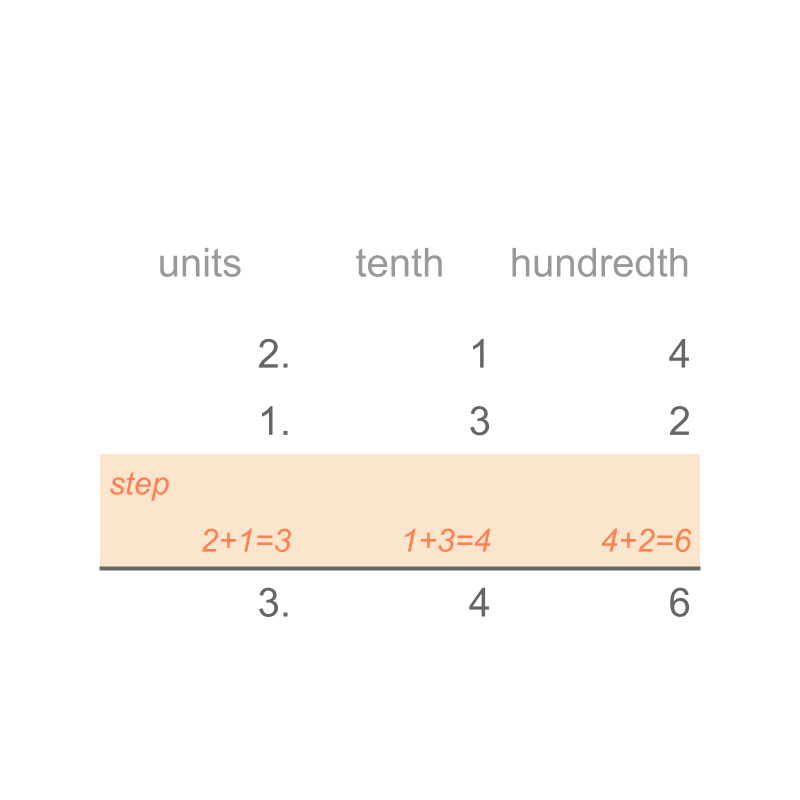
The difference $1.56 - 0.88$ $1.56 - 0.88$ is " $0.68$ $0.68$ ".

By first principles, the subtrahend amount is taken-away from minuend. When subtrahend is greater than the minuend, the immediate larger place-value of minuend is de-grouped before subtraction.

A simplified procedure is designed to represent the subtraction by first principles.

Consider the subtraction $1.56 - 0.88$ $1.56 - 0.88$ .
The digits of the numbers are aligned by place-value. Note that $5$ $5$ of tenth place-value is aligned to $8$ $8$ of tenth place value. The digits are subtracted in place-value starting from lowest place-value hundredth. The subtrahend $8$ $8$ count is larger than the minuend $6$ $6$ counts. This leads to de-grouping or borrowing before performing subtraction.

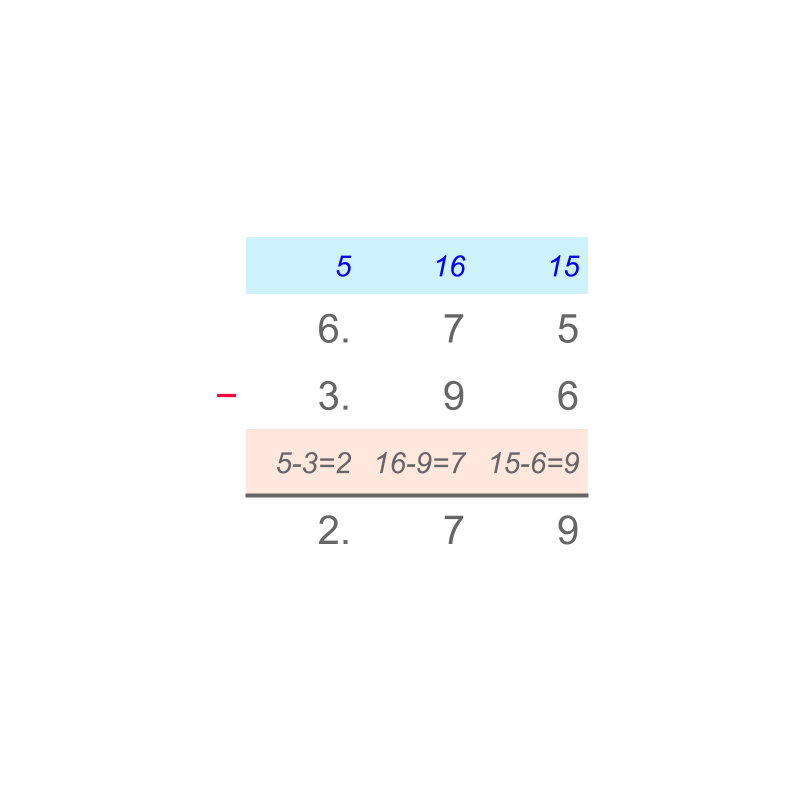
The difference $6.75 - 3.96$ $6.75 - 3.96$ is " $2.79$ $2.79$ ". The simplified procedure is given in the figure.

simplification

Addition of Decimals Decimals are directed numbers with positive or negative sign.

The Sign-property of Integer Addition is applicable to Decimals
positive + positive is simple addition of absolute values
positive + negative is subtraction of smaller absolute value from larger one with result having sign of number with larger absolute value
negative + negative is simple addition of absolute values with result having negative sign.

The addition of absolute values is performed as per Addition by Place-value with regrouping.

The subtraction of absolute values is performed as per Subtraction by Place-value with de-grouping.

The extended place-value order for decimals is used.
$\dots <$ $cdots <$ hundredth $<$ $<$ tenth $<$ $<$ units $<$ $<$ tens $<$ $<$ hundreds $< \dots$ $< cdots$

Subtraction of Decimals : Decimals are directed numbers with positive or negative sign. Subtraction is handled as addition of minuend and negative of subtrahend.
That is, the above procedure for addition is followed after converting subtraction to addition.

examples

Find the sum of $- 0.6$ $-0.6$ and $0$ $0$ .
The answer is " $- .6$ $-.6$ "

Find the sum of $1.1$ $1.1$ and $- .140$ $-.140$
The answer is " $0.96$ $0.96$ "

Find the sum of $.2$ $.2$ and $- .2$ $-.2$
The answer is " $0$ $0$ "

Find the sum of $- 23.45$ $-23.45$ and $- 8.89$ $-8.89$
The answer is " $- 32.34$ $-32.34$ "

Find the difference $- 0.6 - 0$ $-0.6- 0$ .
The answer is " $- .6$ $-.6$ "

Find the difference of $- 1.1 - .140$ $-1.1-.140$
The answer is " $- 1.24$ $-1.24$ "

Find the difference $.2 - (- .2)$ $.2 - (-.2)$
The answer is " $0.4$ $0.4$ "

Find the difference $- 23.45 - (- 8.89)$ $-23.45-(-8.89)$
The answer is " $- 14.56$ $-14.56$ "

summary

Addition of Decimals Decimals are directed numbers with positive or negative sign.

The Sign-property of Addition is applicable to Decimals
positive + positive is simple addition of absolute values
positive + negative is subtraction of smaller absolute value from larger one with result having sign of number with larger absolute value
negative + negative is simple addition of absolute values with result having negative sign.

The addition of absolute values is performed as per Addition by Place-value with regrouping.

The extended place-value order for decimals is used.
$\dots <$ $cdots <$ hundredth $<$ $<$ tenth $<$ $<$ units $<$ $<$ tens $<$ $<$ hundreds $< \dots$ $< cdots$

The subtraction of absolute values is performed as per Subtraction by Place-value with de-grouping.

Subtraction of Decimals : Decimals are directed numbers with positive or negative sign. Subtraction is handled as addition of minuend and negative of subtrahend.
That is, the above procedure for addition is followed after converting subtraction to addition.

Outline

The outline of material to learn "decimals" is as follows.

Note: goto detailed outline of Decimals

• Decimals - Introduction

→ Decimals as Standard form of Fractions

→ Expanded form of Decimals

• Decimals - Conversion

→ Conversion between decimals and fractions

→ Repeating decimals

→ Irrational Numbers

• Decimals - Arithmetics

→ Comparing decimals

→ Addition & Subtraction

→ Multiplication

→ Division

• Decimals - Expressions

→ Expression Simplification

→ PEMA / BOMA