Whole Numbers : Division : Simplified Procedure for Large Numbers

maths > wholenumbers

Division : Simplified Procedure for Large Numbers

what you'll learn...

overview

The division in first principles was explained as splitting of dividend into divisor number of parts. In that, one part is the quotient and the part of dividend that could not be split is the remainder. division simplified procedure This method is revised for 2-digit numbers and established the de-grouping is required. A simplified procedure for large numbers is explained.

de-grouping

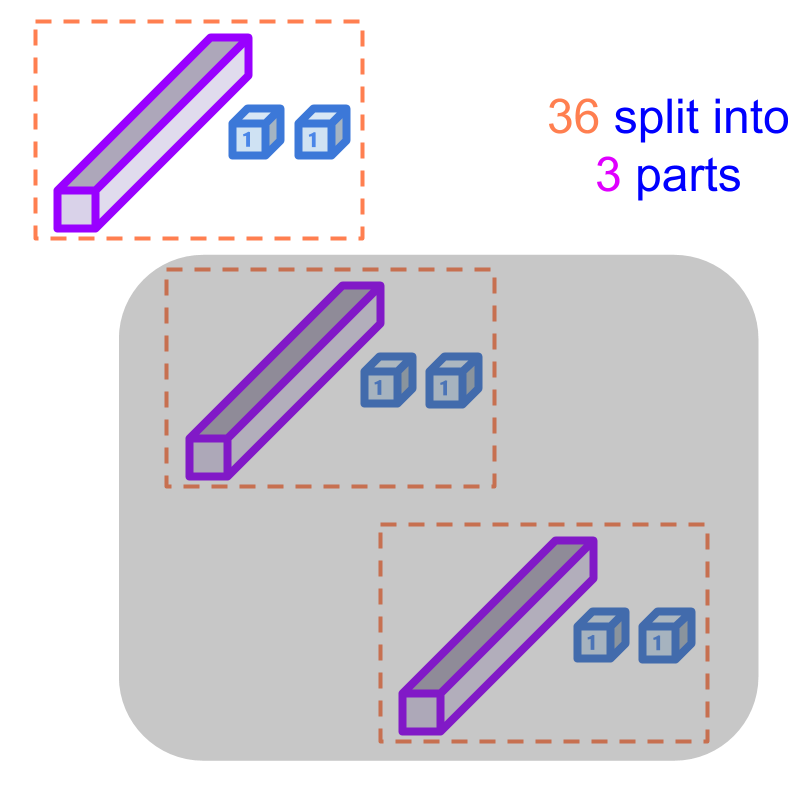
Consider the division $36 \div 3$ $36-:3$ . To perform the division, $36$ $36$ is split into $3$ $3$ parts and one part is counted.

Considering the division $36 \div 3$ $36-:3$ . Splitting $36$ $36$ into $3$ $3$ parts is shown in the figure. Only one part is chosen, and other parts are shaded.

There are $1$ $1$ tens and $2$ units which together form the value $12$ in one part.

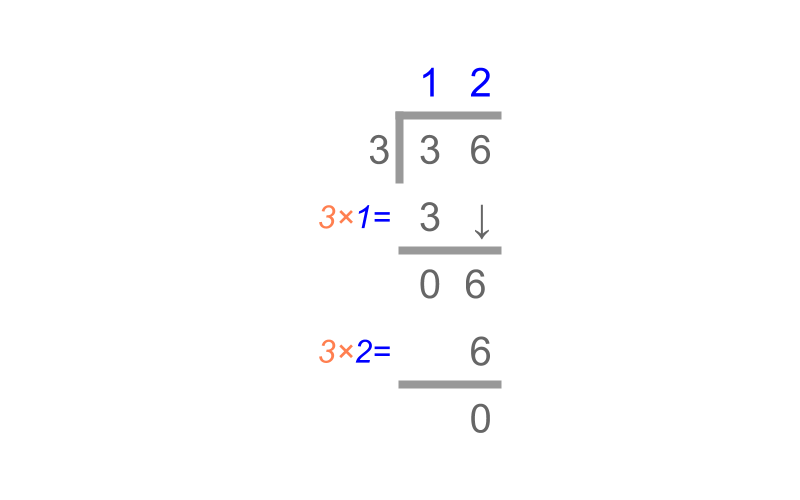
division two digit numbers place-value-form

Considering the division $36-:3$ . The number $36$ is given in the place value form in the figure. The splitting into equal parts is visualized and the division is performed as shown in the figure.

The tens place is divided first as $3-:3=1$ and then the units place is divided as $6-:3=2$ .

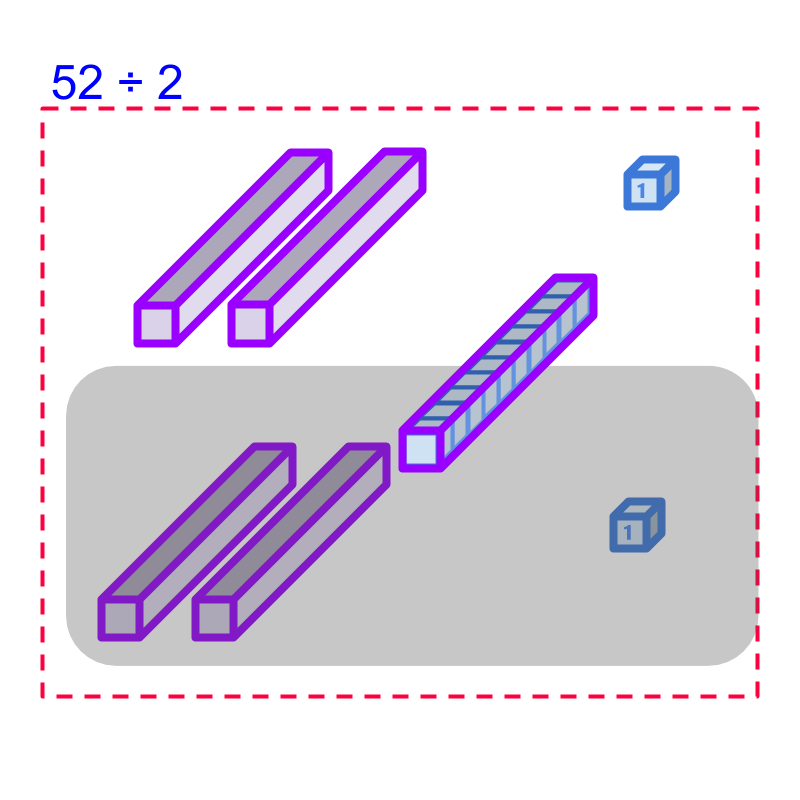
division with carryover two digit numbers

Consider the division $52-:2$ . That is, $52$ is split into two equal parts as shown in the figure.

$5$ tens are distributed as $2$ each in the two parts. $1$ ten part remains in the dividend. The $2$ units parts are distributed as $1$ each in the two parts.

$1$ ten is equivalently $10$ units and so can be distributed as $5$ units each.

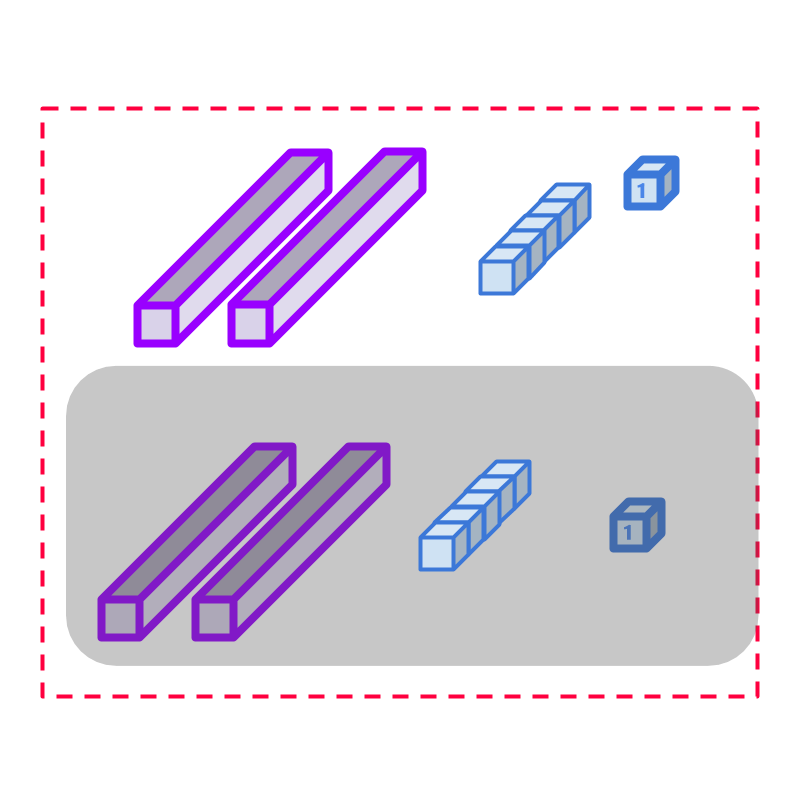
Considering the division $52-:2$ . That is, $52$ is split into two equal parts as shown in the figure. Note that $1$ ten remaining in dividend is de-grouped into $10$ units and are placed $5$ each. So the result of the division is $2$ tens and $6$ units, which is $26$ .

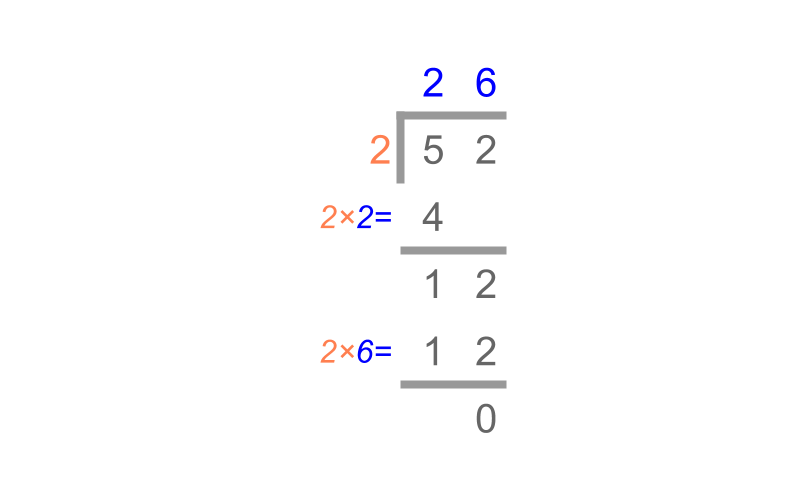
Considering the division $52-:2$ . The number $52$ is given in the place value format in the figure.

A simplified procedure, Division by Place-value is shown in the figure.

First the tens place division, $5-:2$ is considered. $2xx2=4$ and $1$ ten remains.

The remaining $1$ ten is converted to $10$ units and combined with $2$ units from units place of dividend. In the units place, $2xx6=12$ is applied. The result is $26$ .

simplify

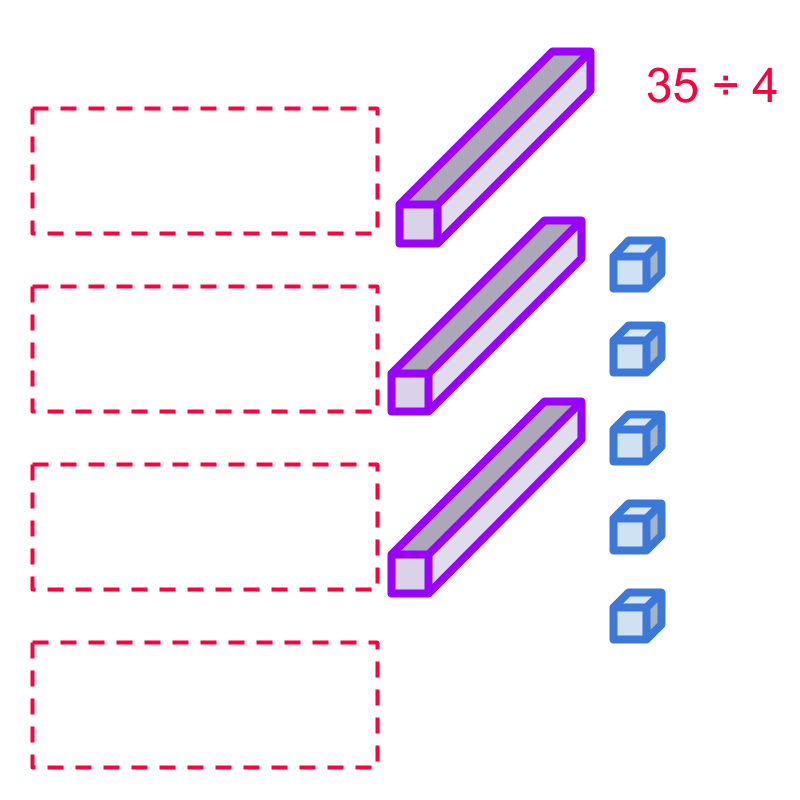
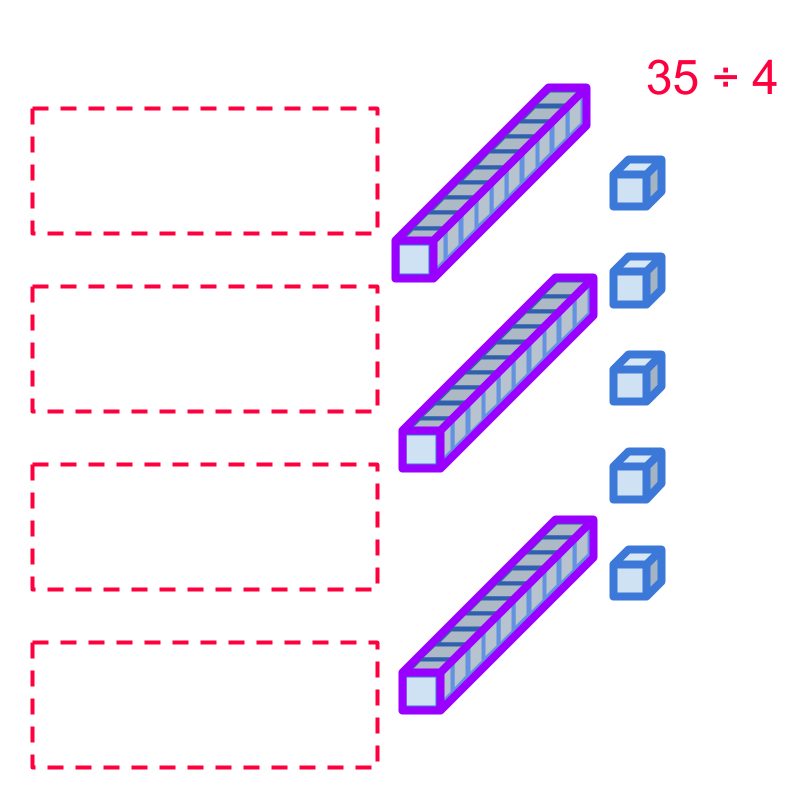
Consider the division, $35-:4$ . One $35$ is shown in the figure.

The dividend can be either split into $4$ equal parts or the simplified procedure can be used to divide in place-value form.

Considering the division: $35-:4$ .

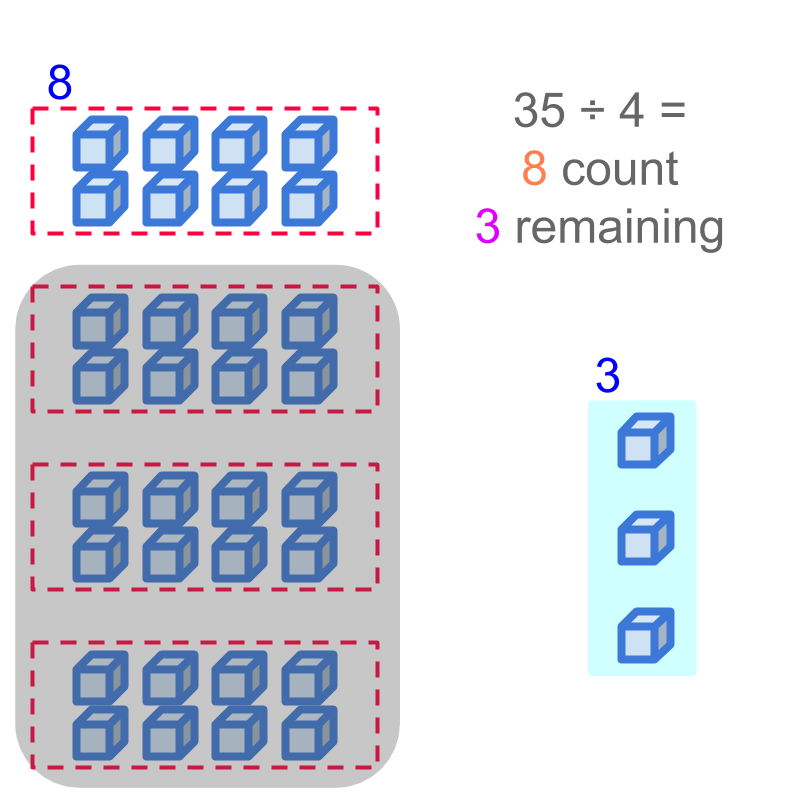
The $3$ tens cannot be split into $4$ equal parts. So the $3$ tens are de-grouped into $30$ units and combined with the $5$ units.

Considering the division: $35-:4$ . The value $35$ is converted into $30$ units and combined with the $5$ units in the units place. Now, the units are distributed as shown in the figure.

One part makes $8$ units and $3$ units of dividend is remaining. The result of the division is, quotient $8$ and remainder $3$ .

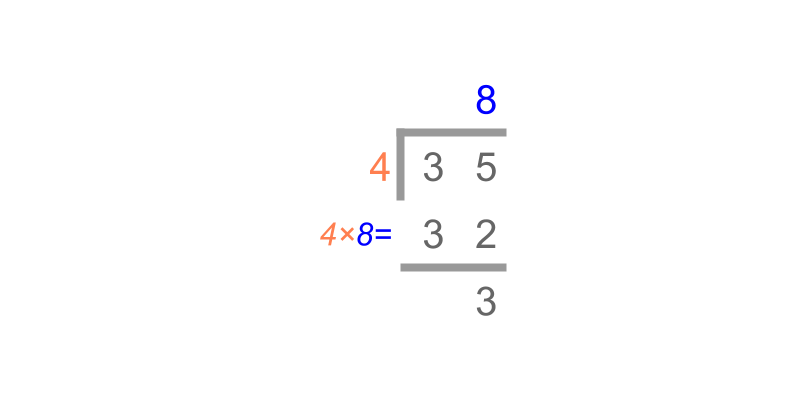
division of larger two digit numbers place value

Considering the division: $35-:4$ . The numbers are given in place value in the figure. A simplified procedure is given in the figure. The result of the division is, quotient $8$ and remainder $3$ .

Division by Place-value -- Simplified Procedure : A number is divided using long division method as shown in the figure.
Note: The procedure de-groups remaining tens into equivalent number of $10$ units.

example

What is the quotient and remainder of $1111 -: 4$ ?
The answer is "quotient $277$ and remainder $3$ "

What is the quotient and remainder of $3001 -: 3$ ?
The answer is "quotient $1000$ and remainder $1$ "

summary

Division by Place-value -- Simplified Procedure : A number is divided using long division method as shown in the figure. simplified process for division Note: The procedure de-groups remaining tens into equivalent number of $10$ units.

Outline

The outline of material to learn whole numbers is as follows

Note: click here for detailed outline of Whole numbers

• Introduction

→ Numbers

→ Large Numbers

→ Expanded form

→ Face and place values

→ Approximation and Estimation

• Comparison

→ Comparing two numbers

→ Number line

→ Predecessor & Successor

→ Largest & Smallest

→ Ascending & Descending

• Addition Subtraction

→ Addtion: First Principles

→ Addition: Simplified Procedure

→ Subtraction: First Principles

→ Subtraction: Simplified Procedure

• Multiplication Division

→ Multiplication: First Principles

→ Multiplication: Simplified Procedure

→ Division: First Principles

→ Division: Simplified Procedure

• Numerical Expression

→ Introducing Numerical Expressions

→ Precedence

→ Sequence

→ Brackets