Whole Numbers : Addition: Simplified Procedure for Large Numbers

maths > wholenumbers

Addition: Simplified Procedure for Large Numbers

what you'll learn...

overview

The addition in first principles was explained as combining two quantities and counting or measuring the combined quantity. addition simplified procedure This method is revised for 2-digit numbers and established that the tens place and units place can be combined separately. This sets up learning addition by place-value.

In doing the addition by place-value, the count at a place-value can be more than $9$ $9$ and that sets up learning regrouping. The regrouping is explained as the carry-over in addition.

regrouping

Consider addition of, $12$ $12$ and $15$ $15$ . The quantities are combined together and the combined quantity is counted.

Combining $12$ $12$ and $15$ $15$ is shown in the figure. The top shaded portion shows the numbers $12$ $12$ and $15$ $15$ .The combined quantity is shown in the lower half. The combined quantity is: $2$ tens and $7$ units. The result is $27$ .

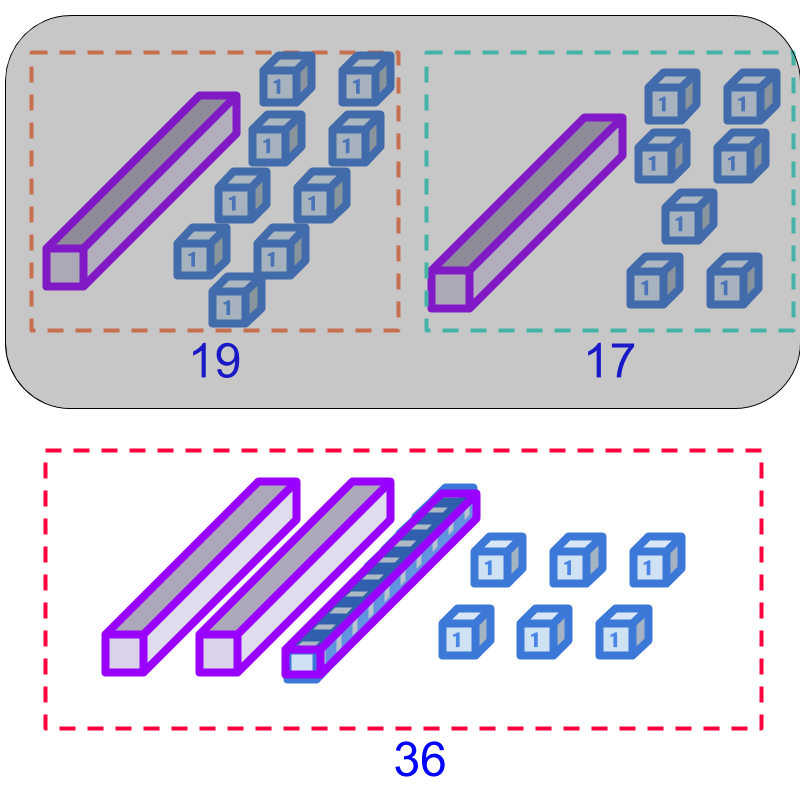
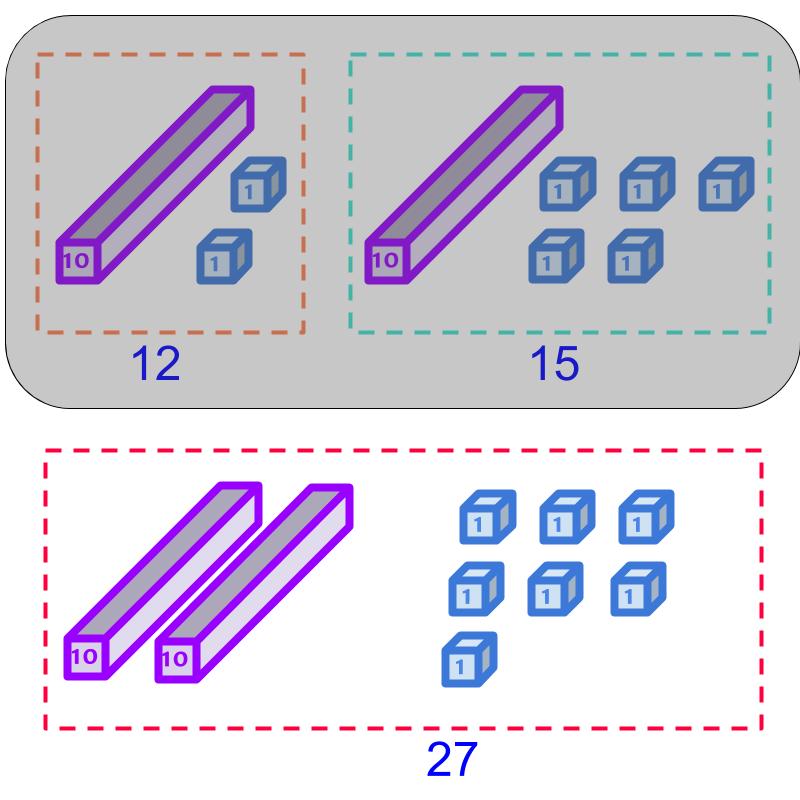
Consider the addition of $19$ and $17$ . The quantities are illustrated in the figure. Counting the two quantities together, there are $2$ tens and $16$ units. The units can be re-grouped into tens.

Considering the addition of $19$ and $17$ .

The combined sum is illustrated in the lower portion of the figure. Note that $10$ units are combined together to form the $1$ ten. So the result of the addition is $36$ .

$10$ units blocks are grouped into $1$ ten. This is referred as regrouping.

Note that, the two numbers $19$ and $17$ were grouped already and when combined, the number representing the sum is regrouped.

Regrouping: In a place value position, when combining grouped numbers, $10$ of a lower place-value can be regrouped into $1$ of the next higher place-value.

simplify

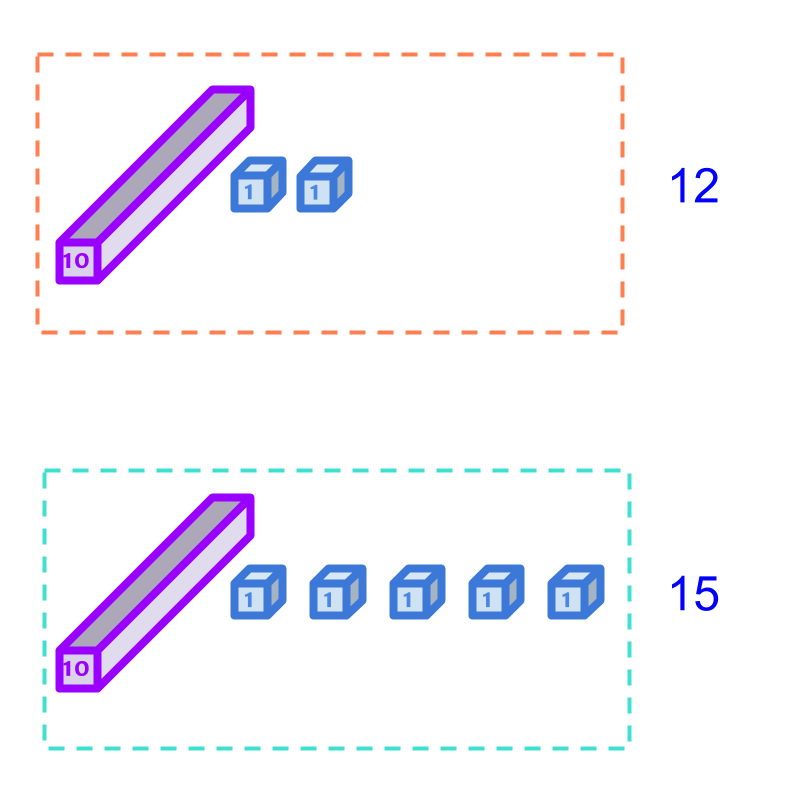
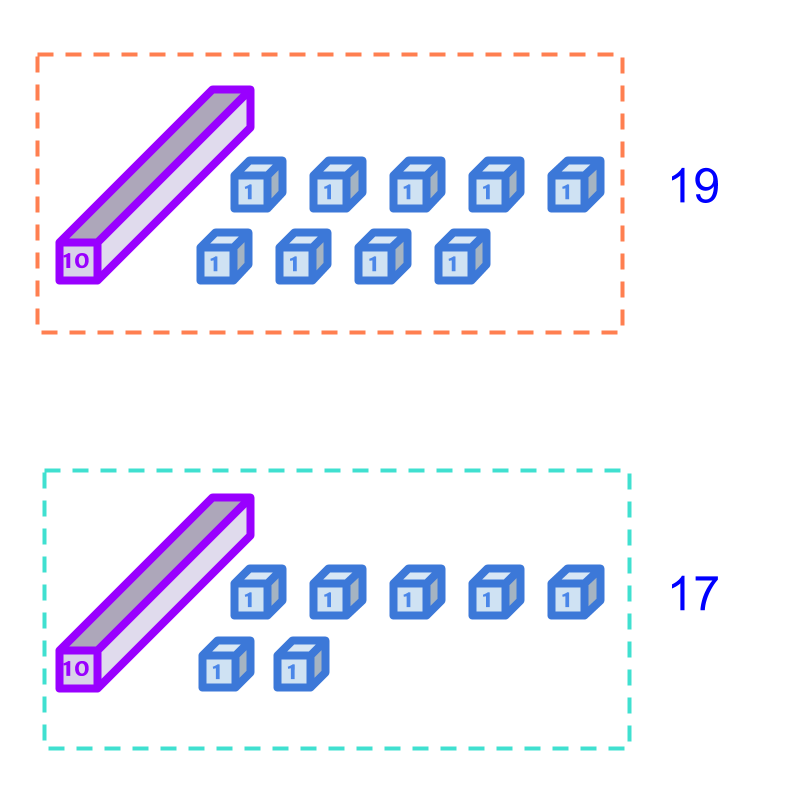
Considering the addition of $19$ and $17$ .

A simplified procedure for addition is shown in the figure.

$9$ and $7$ are added to $16$ . The $10$ units are converted to $1$ ten and moved to the tens position.

The sum is calculated as $36$ .

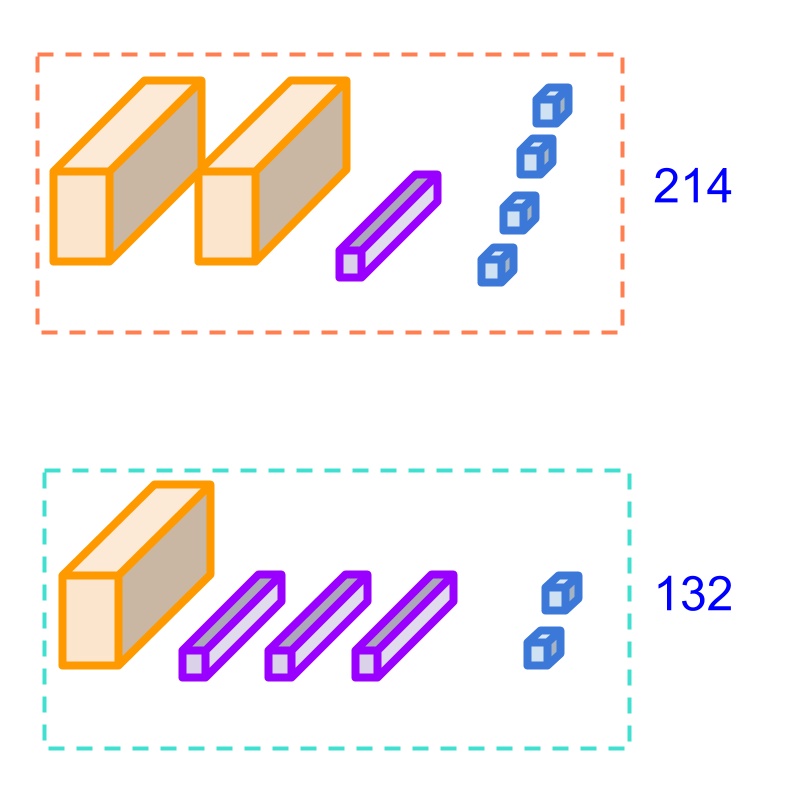
Consider the addition of $214$ and $132$ . We can count the combined quantity in the figure. The combined quantity is counted as,

$4$ units and $2$ units together is $6$ units,

$1$ tens and $3$ tens together is $4$ tens,

$2$ hundreds and

$1$ hundred together is $3$ hundreds.

So the combined count is $346$ .

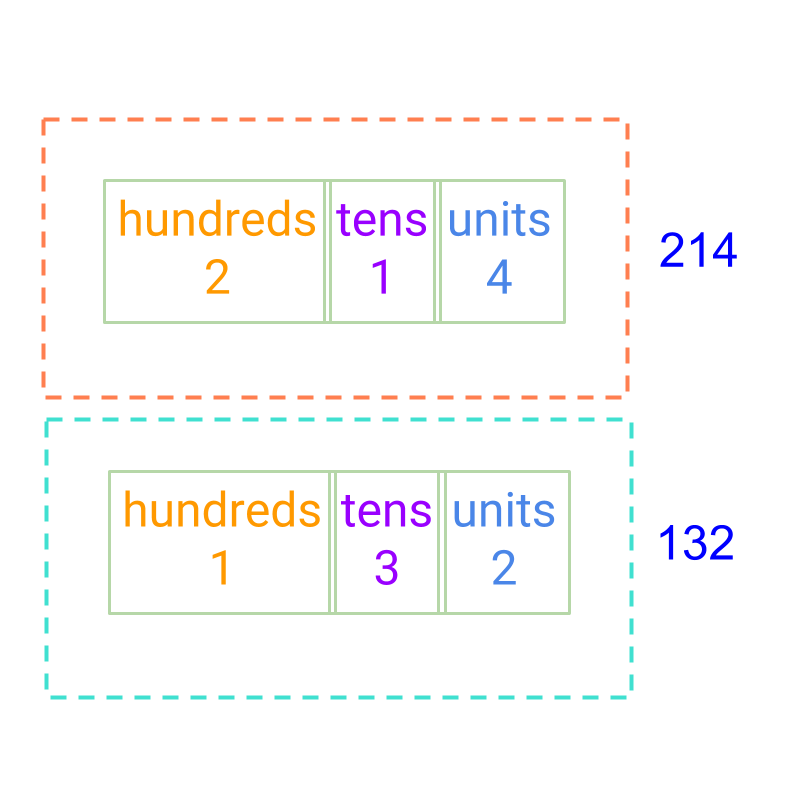
The numbers $214$ and $132$ are given in the place-value form. Addition is carried out and

The result if $346$ .

The simplified procedure is given in the figure.

The digits in the units place are added.

Then the digits in the tens place are added.

Then the digits in the hundreds place are added.

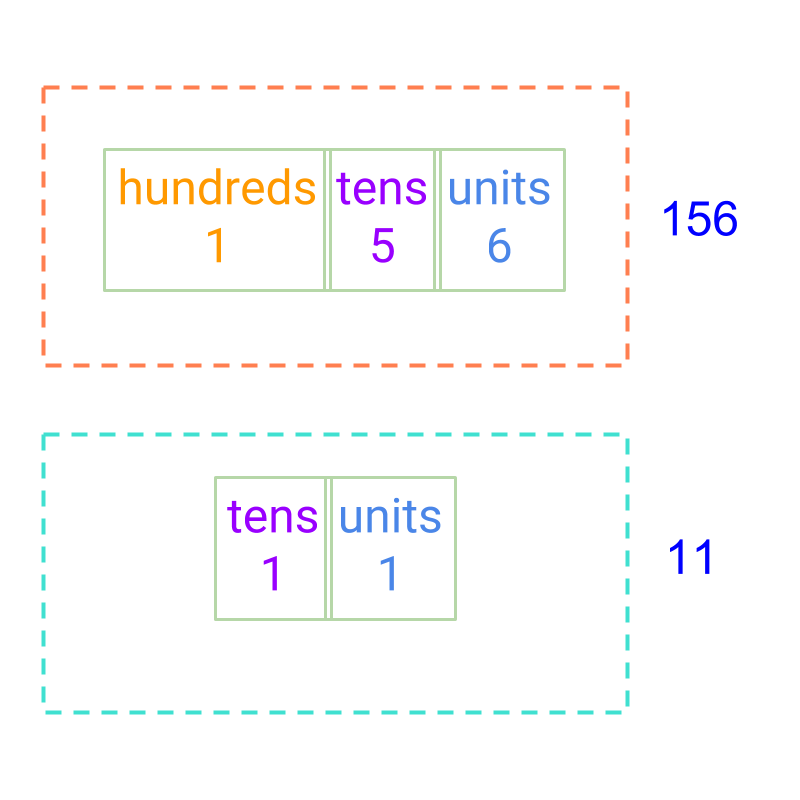
Considering the addition of $156$ and $11$ . The result is $167$ , and not 266. The place value positions should be aligned correctly when employing the simplified procedure.

Considering the addition of $156$ and $88$ . The simplified procedure Addition by Place-value with regrouping is given in the figure.

• The digits in units place are added. $6+8=14$ . $14$ units is modified as $1$ ten and $4$ units. The $1$ ten is moved to the tens place as carry over. The $4$ units is placed in the units place of sum.

• The tens place is modified $1+5+8 = 14$ . $14$ tens is modified as $1$ hundred and $4$ tens. The $1$ hundred is moved to the hundreds place as carry over. The $4$ tens is placed in the tens place of sum.

• The hundreds place is modified $1+1 = 2$ . $2$ hundreds is placed in the hundreds place of the sum.

The result of addition is $244$

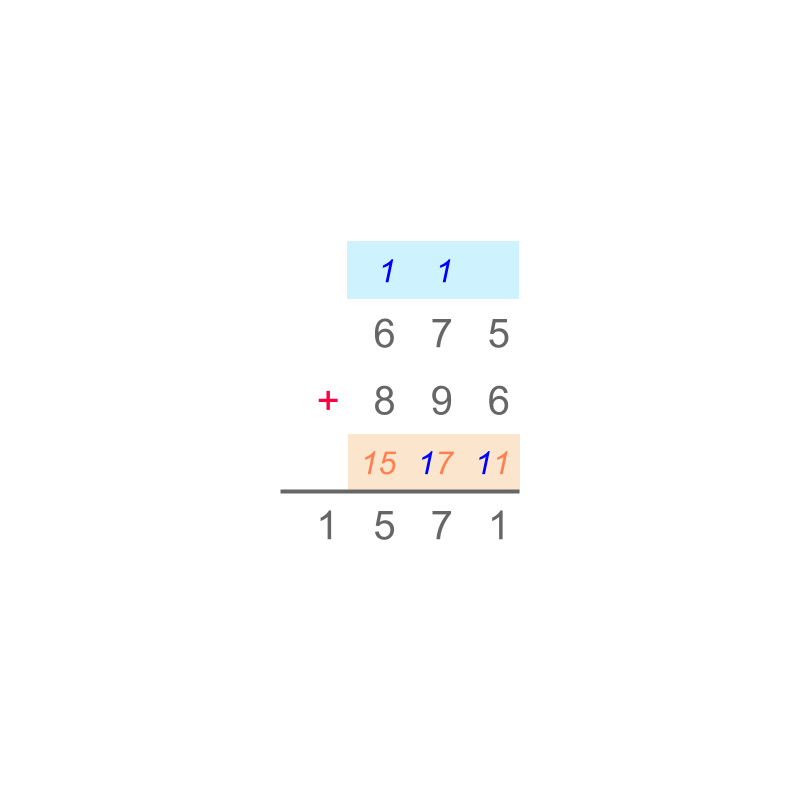
Consider the addition of two numbers. The simplified procedure Addition by Place-value with regrouping is given in the figure. Note: the addition of place values and the carry over are highlighted in color.

The result of addition is $1571$ .

Addition by Place-value with regrouping -- simplified procedure : Two numbers are added as follows:

• the place-value positions are arranged units under units, $10$ s under $10$ s, etc.

• the units are added and if the result has $10$ numbers, then it is carried to the $10$ s place.

• The addition is continued to the higher place-value position.

Note: The carry over is the simplification of combining $10$ of a place value to a higher place value.

examples

What is the sum of $2314+2883$ ?
The answer is " $5297$ "

What is the sum of $34+66$ ?
The answer is " $100$ "

summary

Addition by Place-value with regrouping -- simplified procedure : Two numbers are added as follows:

• the place-value positions are arranged units under units, $10$ s under $10$ s, etc.

• the units are added and if the result has $10$ numbers, then it is carried to the $10$ s place.

• The addition is continued to the higher place-value position. addition simplified procedure The carry over is the simplification of combining $10$ of a place value to a higher place value.

Outline

The outline of material to learn whole numbers is as follows

Note: click here for detailed outline of Whole numbers

• Introduction

→ Numbers

→ Large Numbers

→ Expanded form

→ Face and place values

→ Approximation and Estimation

• Comparison

→ Comparing two numbers

→ Number line

→ Predecessor & Successor

→ Largest & Smallest

→ Ascending & Descending

• Addition Subtraction

→ Addtion: First Principles

→ Addition: Simplified Procedure

→ Subtraction: First Principles

→ Subtraction: Simplified Procedure

• Multiplication Division

→ Multiplication: First Principles

→ Multiplication: Simplified Procedure

→ Division: First Principles

→ Division: Simplified Procedure

• Numerical Expression

→ Introducing Numerical Expressions

→ Precedence

→ Sequence

→ Brackets