Whole Numbers : Comparing two Whole Numbers

maths > wholenumbers

Comparing two Whole Numbers

what you'll learn...

overview

In this page, comparison of two whole numbers is explained in the following two forms.

• lesson outline

Trichotomy Property

Whole numbers are used to represent count or measure of quantities.

Comparing the number of fish and cats in the figure, it is found that, number of fish is more than number of cats.

That is $10$ $10$ is larger than $5$ $5$ . .

number of cars is equal to the number of cats.

That is $5$ $5$ equals $5$ $5$ .

number of cats is lesser than number of fish.

That is $5$ $5$ is less than $10$ $10$

Whole numbers are used to measure quantities. An example is height of a tree.

The pine tree, shown in picture, is taller than the palm tree shown in the picture.

Such measurement of quantities or numbers can also be compared for smaller and equal.

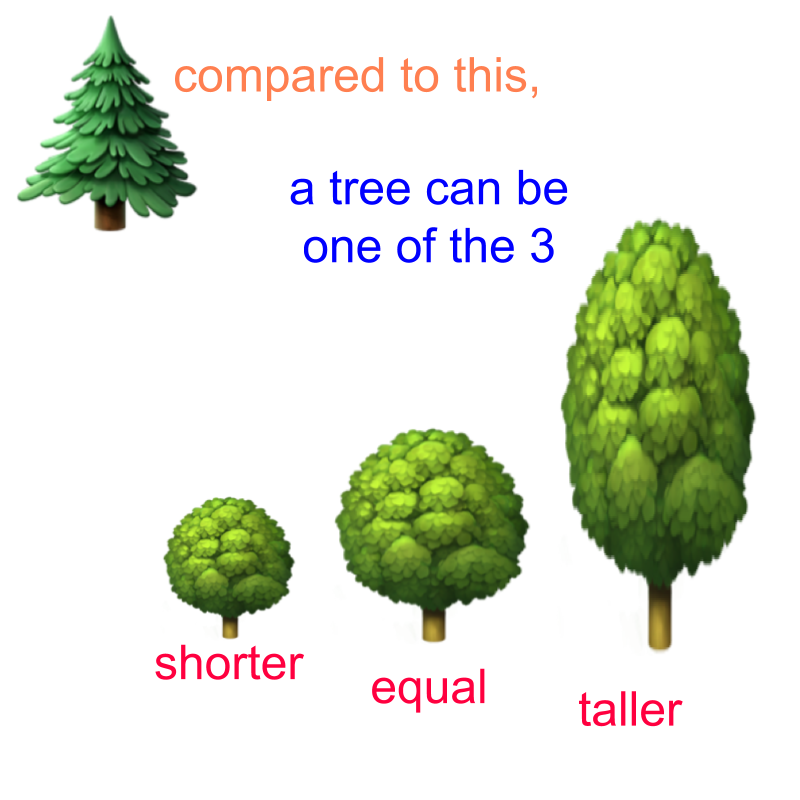
One of the following is true while comparing two quantities.

• A quantity is lesser than another.

• A quantity equals another.

• A quantity is more than another.

For example,
• $4$ $4$ is lesser than $5$ , which is given as $4 < 5$

• $5$ equals $5$ , which is given as $5=5$

• $5$ is more than $4$ , which is given as $5>4$

When compared to a number, another number can only be one of the three,
(1) smaller,
(2) equal, or
(3) larger

$3<7$

The symbol $<$ is used to denote the number on the left side is less than the number on the right. In this case, 3 is less than 7.

$7>3$

The symbol $>$ is used to denote the number on the left side is greater than the number on the right. In this case, 7 is greater than 3.

$3=3$

The symbol $=$ is used to denote the number on the left side equals the number on the right. In this case, 3 equals 3.

Comparison in First Principles

Considering numbers $7$ and $8$ . There are $7$ burgers and $8$ dogs in the figure.

Consider comparing $8$ and $7$ . The comparison of numbers as quantities is illustrated in the figure. In first principles, two quantities are matched one-to-one. The quantity that has excess is greater. The other quantity is smaller. If the two quantities match to the last count, then they are equal.

Number of dogs have one excess, so number of dogs is greater than the number of burgers.

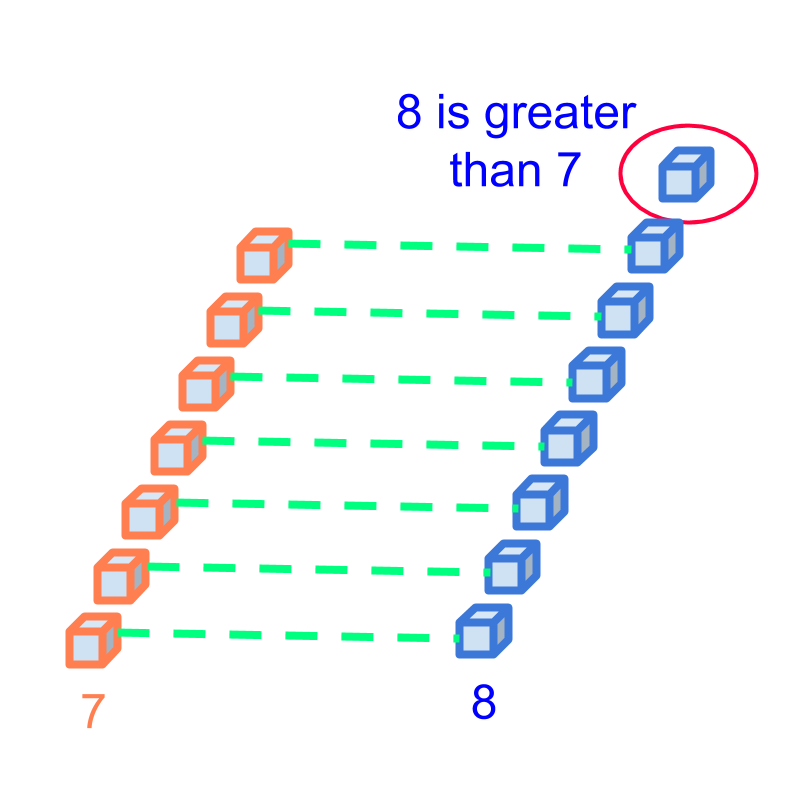
Consider comparing $8$ and $7$ . The comparison of numbers as quantities is illustrated in the figure.

The quantity that has excess is greater. And

The the other quantity is lesser.

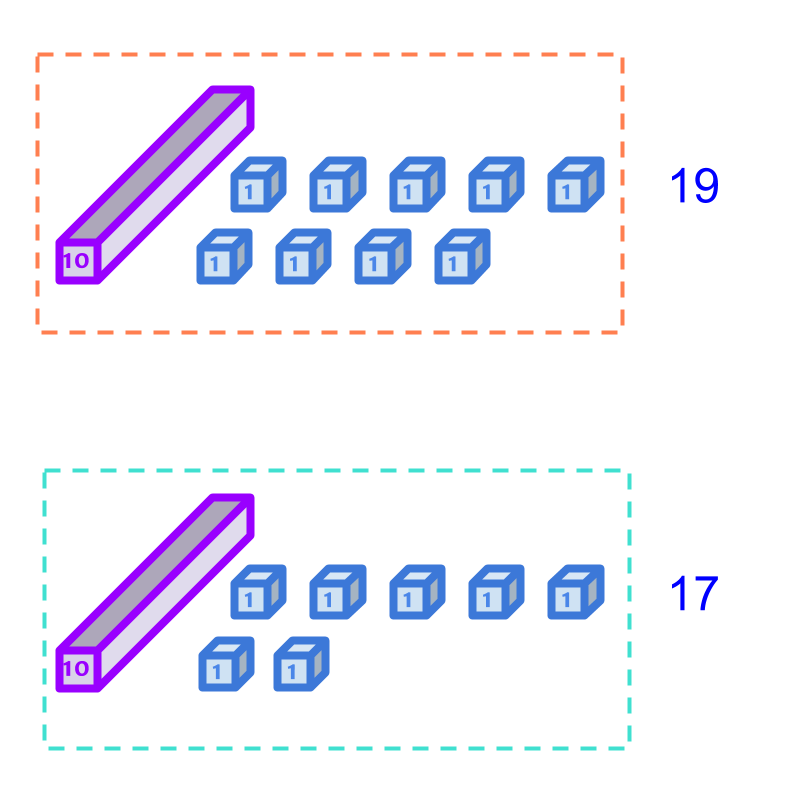
Comparison of two numbers $19$ and $17$ is illustrated in the figure. Which one is smaller?

On comparing the quantities, $17$ is found to be smaller.

Comparing $19$ and $17$ . By first principles: The quantities are matched. The tens is made of 10 units. So first the tens, given in purple bar, are matched one-to-one. Then the units, given in blue cubes, are matched and found that $19$ has excess. So $17$ is found to be smaller.

Compare numbers $47$ and $53$ . Which one is larger?
The answer is " $53$ ".

Simplified Procedure : Comparison by place-value

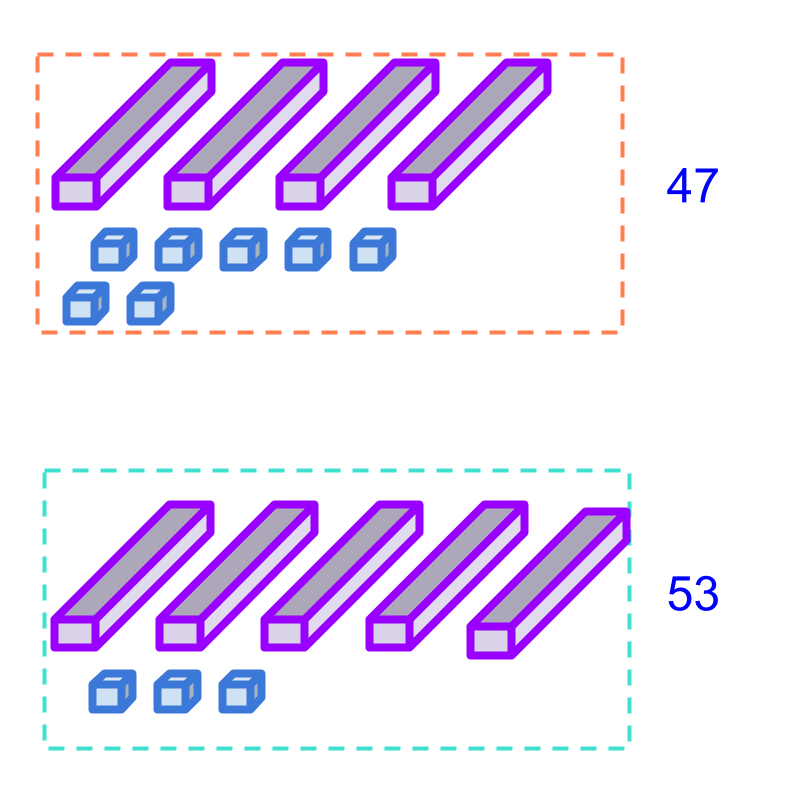
Comparing the numbers $47$ and $53$ .

By first principles : The quantities are matched. A ten is made of 10 units. The tens, given in purple bar, are matched one-to-one. From this, $53$ is found to be larger.

As a simplified procedure : Comparison by place-value, the numbers in tens place value can be compared. $4$ in $47$ and $5$ in $53$ . On comparing, $53$ is found to be larger.

Note that once it is found that the tens place are not equal, the larger number is decided. The units place does not need to be compared.

Compare numbers $214$ and $132$ . Which one is larger?
The answer is " $214$ "

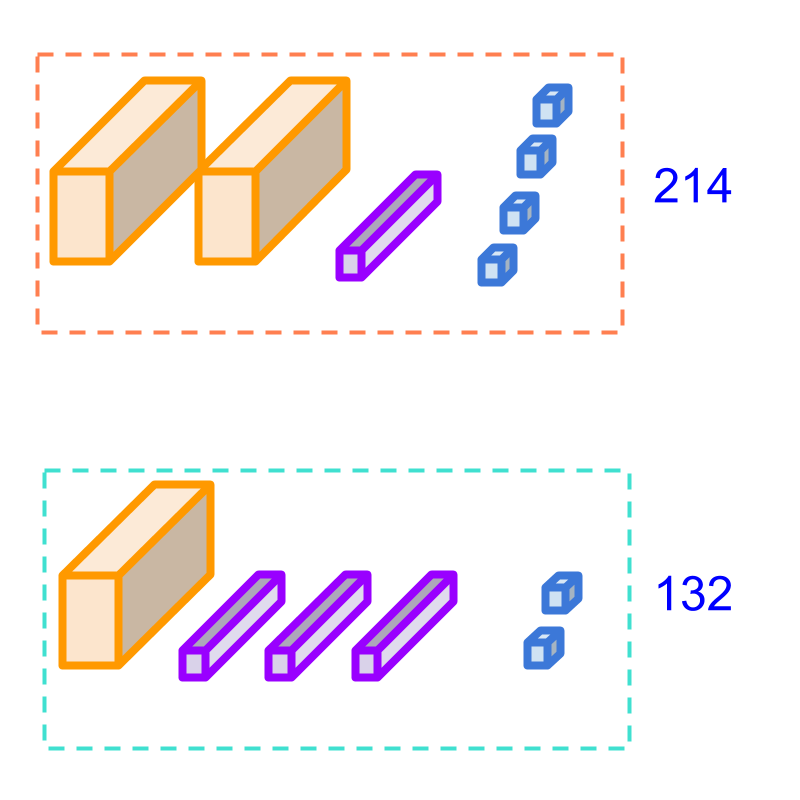
Comparing numbers $214$ and $132$ .

By First principles, the two quantities are matched. The hundreds are the largest among the three and made of $10$ tens. So the hundreds are matched. From this, $214$ is found to be larger.

As a simplified procedure: Comparison by place-value, the numbers in hundreds place are compared first. $2$ from $214$ is compared with $1$ from $132$ . Since $2$ is greater than $1$ , it is concluded that the $214$ is larger.

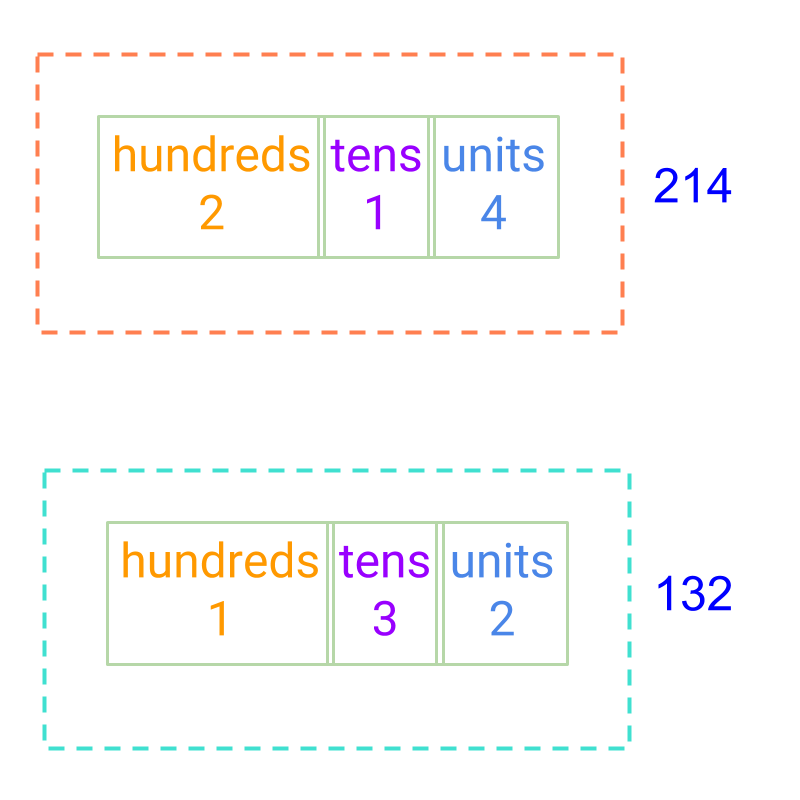
Comparing numbers $214$ and $132$ .

The numbers are given in the place-value form. Comparing the hundreds place, $2$ is greater than $1$ , it is concluded that the $214$ is larger.

Compare numbers $156$ and $88$ . Which one is smaller?
The answer is "Comparing $1$ of $156$ and $0$ of $088$ , $88$ is smaller"

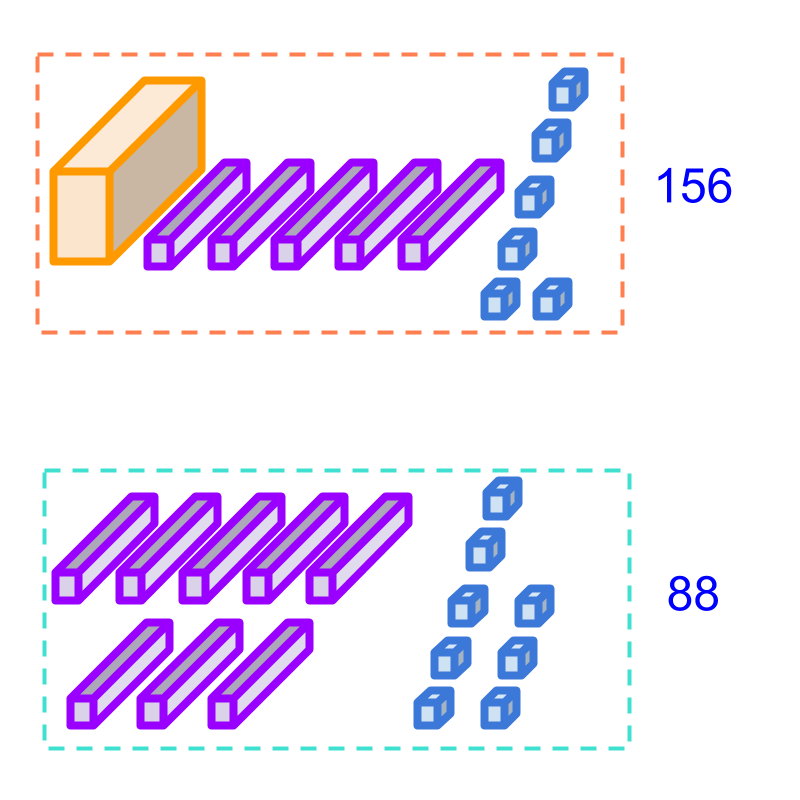
Comparing $156$ and $88$ . It is noted that the hundreds place is $0$ for $88$ .

By the simplified procedure, the digits in the hundreds place are compared and $0$ is smaller than $1$ . It is concluded that $88$ is smaller.

As a Simplified Procedure : Comparison by place-value , the numbers in tens place value can be compared. $1$ in $19$ and $1$ in $17$ . Both digits in tens place are equal. Then the numbers in the units position are compared. $9$ in the $19$ and $7$ in $17$ . On comparing, $17$ is found to be smaller.

Which of the following is larger than the other? $23$ or $61$ .
The answer is " $61$ " or $61 > 23$

Which of the following is smaller than the other? $2183$ or $2661$ .
The answer is " $2183$ " or $2183 < 2661$ .

Which of the following is greater than the other? $341$ or $341$ .
The answer is "the numbers are equal". $341 = 341$

Definitions

Comparison of whole numbers : Two numbers can be compared to find one of them as

• smaller or less

• equal

• greater or larger

When compared to a number, another number can only be one of the three,

(1) smaller,

(2) equal, or

(3) larger

Comparison by First Principle: To find if one number is larger or smaller than another number, the quantities represented by them are compared.

Example: Comparing the numbers $47$ and $53$ . The quantities represented by them is compared in the figure. It is found that $47$ is smaller than $53$ .

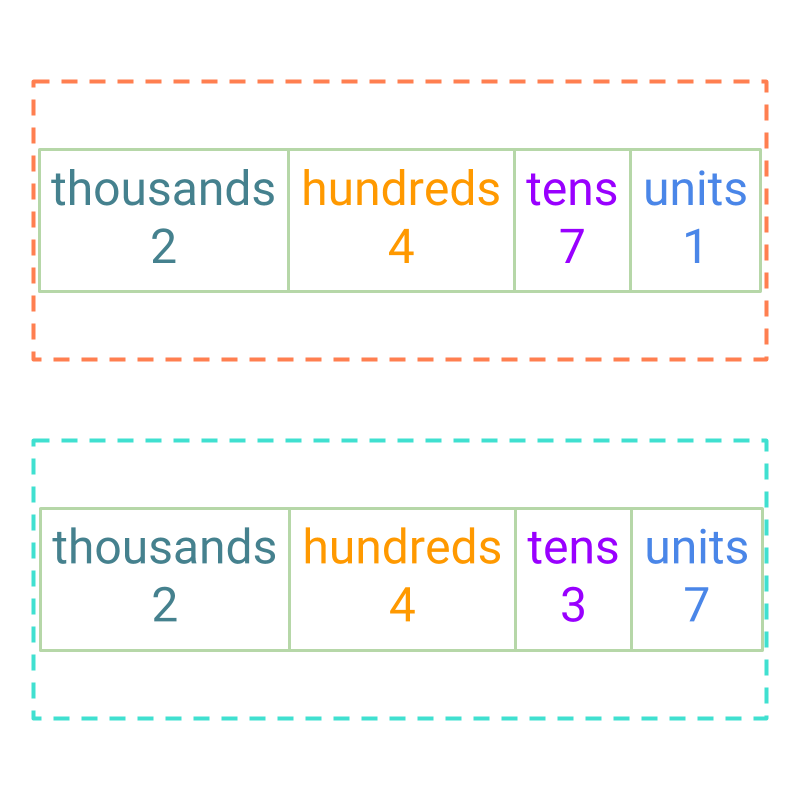
Comparison by Place-value -- Simplified Procedure to Compare Large Numbers: To find if one number is larger or smaller than another number, the digits at the highest place value are compared and if they are equal, then the digits at next lower place value are compared.

For example: Let us take the numbers $2471$ and $2437$ .

Largest place value is $1000$ and the digits are $2$ and $2$ , which are equal.

Next smaller place value is $100$ and the digits are $4$ and $4$ , which are equal.

Next smaller place value is $10$ and the digits are $7$ and $3$ , in which, $7$ is greater than $3$ .

So $2471$ is greater than $2437$ .

Which of the following step help to find the larger between $23$ and $156$ ?

• compare first digits $2$ and $1$ OR

• compare the $100$ s place $0$ and $1$

The answer is "compare the $100$ s place $0$ and $1$ ". The numbers are equivalently given as $023$ and $156$ .

summary

Comparison : Two numbers can be compared to find one of them as

• smaller or less

• equal

• greater or larger

Comparison by First Principle: Two quantities are matched one-to-one and compared in the count or magnitude of the quantities. As a result one of them is smaller or equal to or larger to the other. Example: Comparing the numbers $7$ and $8$ . The quantities represented by them is compared in the figure. It is found that $7$ is smaller than $8$ .

Simplified Procedure -- Comparison by ordered-sequence: To find if one numbers is larger or smaller than another number, the numbers are compared using the order $0,1,2,3,4,5,6,7,8,9, 10, 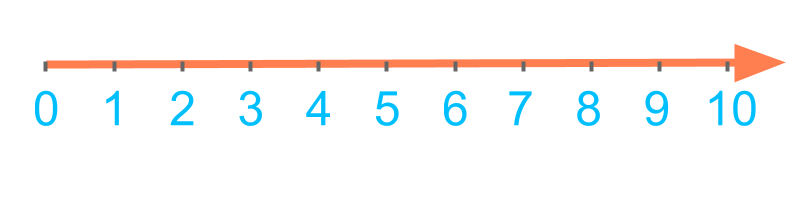cdots$ . Example: Comparing the numbers $4$ and $7$ .

$4$ is on the left-side to $7$ in the order $0,1,2,3,4,5,6,7,8,9$ and so $4$ is smaller than $7$ .

Comparison by Place-value -- Simplified Procedure to Compare Large Numbers: To find if one number is larger or smaller than another number, the digits at the highest place value are compared and if they are equal, then the digits at next lower place value are compared. For example: Let us consider the numbers $2471$ and $2437$ .

Largest place value is $1000$ and the digits are $2$ and $2$ , which are equal.

Next smaller place value is $100$ and the digits are $4$ and $4$ , which are equal.

Next smaller place value is $10$ and the digits are $7$ and $3$ , in which, $7$ is greater than $3$ .

So $2471$ is greater than $2437$ .

A set of symbols $< = >$ are introduced to represent the comparison of two numbers. Consider $2$ and $3$

• $2$ is smaller than $3$ is given as $2<3$

• $2$ equals $1+1$ is given as $2=1+1$

• $3$ is larger than $2$ is given as $3>2$

Outline
The outline of material to learn whole numbers is as follows

Note: click here for detailed outline of Whole numbers

• Introduction

→ Numbers

→ Large Numbers

→ Expanded form

→ Face and place values

→ Approximation and Estimation

• Comparison

→ Comparing two numbers

→ Number line

→ Predecessor & Successor

→ Largest & Smallest

→ Ascending & Descending

• Addition Subtraction

→ Addtion: First Principles

→ Addition: Simplified Procedure

→ Subtraction: First Principles

→ Subtraction: Simplified Procedure

• Multiplication Division

→ Multiplication: First Principles

→ Multiplication: Simplified Procedure

→ Division: First Principles

→ Division: Simplified Procedure

• Numerical Expression

→ Introducing Numerical Expressions

→ Precedence

→ Sequence

→ Brackets