Integers : Integer Multiplication: Simplified Procedure

maths > integers

Integer Multiplication: Simplified Procedure

what you'll learn...

overview

The multiplication in first principles was explained as repetition of integer multiplicand, the integer multiplier number of times. This establishes the simplified procedure : Sign-Property of Integer Multiplication.

regrouping

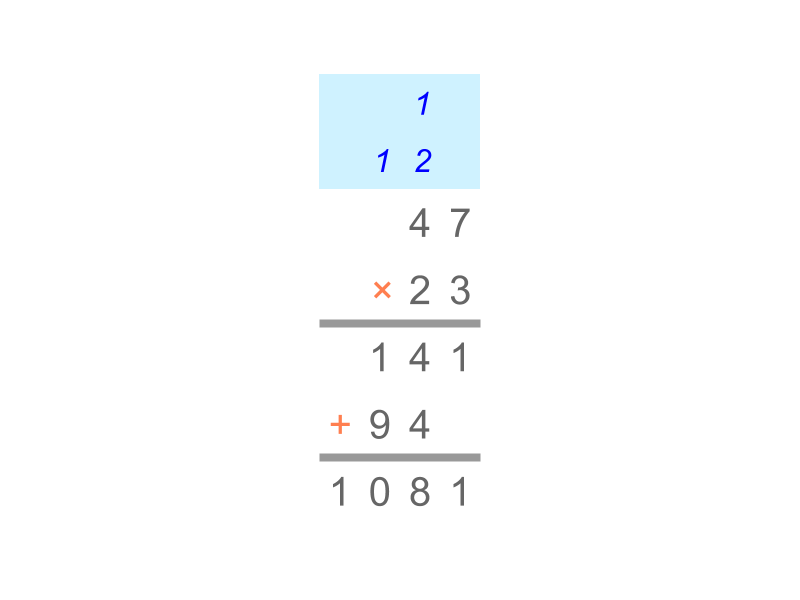
In whole numbers, we had studied the following.

Multiplication by Place-value with Regrouping - Simplified Procedure : Two numbers are multiplied as illustrated in the figure.
Note: The procedure combines $10$ $10$ units into $1$ $1$ ten as carry over and so on for higher place-values.

The product of whole numbers $4 \times 3 = 12$ $4xx3 = 12$ is understood in integers as:

$received: 4$ $text(received:)4$ is repeatedly put in $3$ $3$ times.

The product of integers $- 4 \times 3 = - 12$ $-4 xx 3 = -12$ is understood as $text(given:)4$ is repeatedly put in $3$ times.

The product of integers $4 xx -3 = -12$ is understood as $text(received:)4$ is repeatedly taken away $3$ times.

The product of integers $-4 xx -3 = +12$ is understood as $text(given:)4$ is repeatedly taken away $3$ times.

simplify

Summary of integer multiplication illustrative examples:

• $4xx3 = 12$
$text(received:)4$ is put-in $3$ times

• $(-4)xx3 = -12$
$text(given:)4$ is put-in $3$ times

• $4xx(-3) = -12$
$text(received:)4$ is taken-away $3$ times

• $(-4)xx(-3) = 12$
$text(given:)4$ is taken-away $3$ times

Based on this, the multiplication is simplified as

• +ve $xx$ +ve $=$ +ve

• -ve $xx$ +ve $=$ -ve

• +ve $xx$ -ve $=$ -ve

• -ve $xx$ -ve $=$ +ve

examples

Find the product of the multiplication $22 xx (-1)$
The answer is " $-22$ "

Find the product of the multiplication $0xx(-32)$
The answer is "both the above"

Find the product of the multiplication $-222 xx (-88)$
The answer is "a positive number".

summary

Integer Multiplication -- Simplified Procedure : The sign of the product is decided by signs of multiplicand and multiplier as follows.

Sign-Property of Integer Multiplication
• positive $xx$ positive $=$ positive
• positive $xx$ negative $=$ negative
• negative $xx$ positive $=$ negative
• negative $xx$ negative $=$ positive

The absolute value of the product is calculated by whole number multiplication of absolute values of the multiplicand and multiplier.

Outline

The outline of material to learn integers is as follows.

Note: click here for detailed outline of Integers (directed numbers)

→ Introduction to Directed Numbers

→ Handling Direction

→ Ordinal Property

→ Sign and Absolute Value

→ Comparing Integers

→ Predecessor & Successor

→ Largest & Smallest

→ Ascending & Descending

→ Addition: First Principles

→ Addition: Simplified Procedure

→ Subtraction: First Principles

→ Subtraction: Simplified Procedure

→ Multiplication: First Principles

→ Multiplication: Simplified Procedure

→ Division: First Principles

→ Division: Simplfied Procedure

→ Numerical Expressions with Integers

→ PEMA / BOMA