Integers : Comparing Integers

maths > integers

Comparing Integers

what you'll learn...

overview

In this page, comparison of two integers is explained in the following two forms.

• Comparison or integers (directed whole numbers) in first principles is to compare the quantities by the amount received (the positive direction). Amount given (the negative direction) is smaller than amount received. Larger amount given is smaller than smaller amount given.

• Sign-property of comparison is the simplified procedure which helps in comparing large integers.

recap

In whole numbers, we had studied the following.

Trichotomy Property of Comparison : Two numbers can be compared to find one of them as

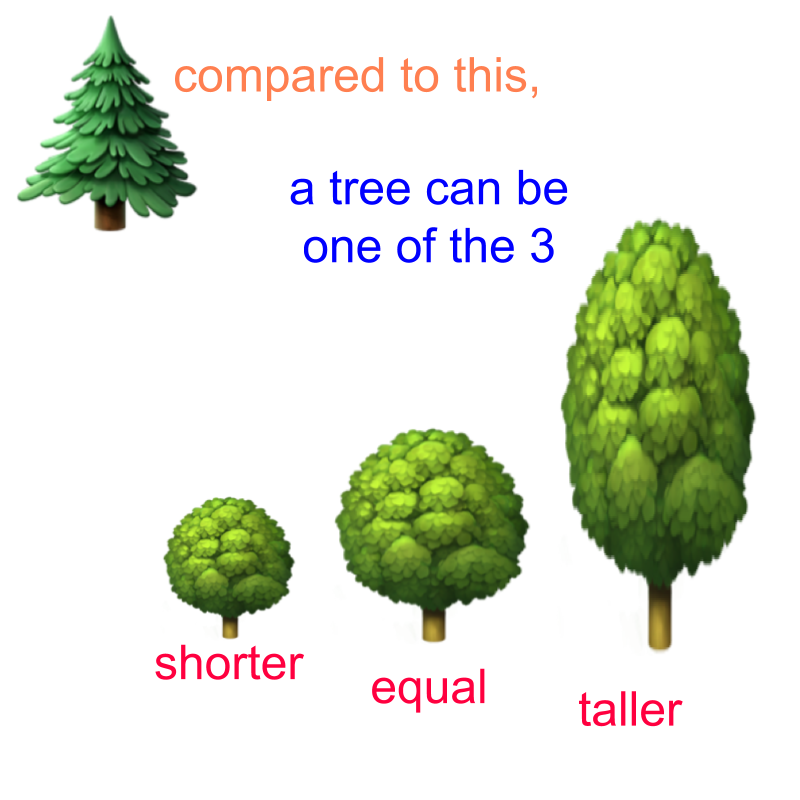
• smaller or less

• equal

• greater or larger

Comparison by First Principle: Two quantities are matched one-to-one and compared in the count or magnitude of the quantities. As a result one of them is smaller or equal to or larger to the other. 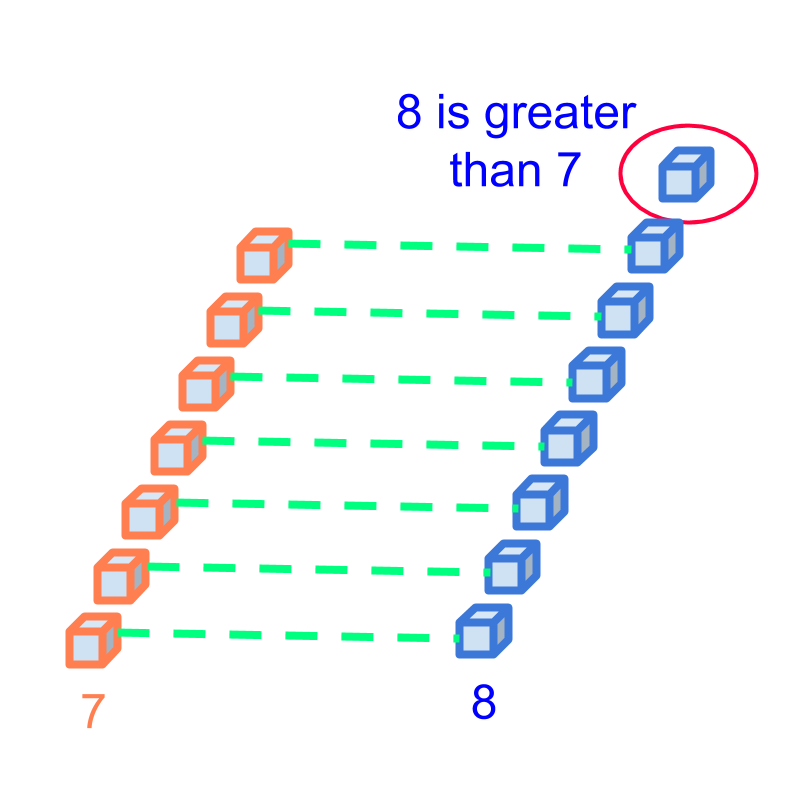whole number comparison Example: Comparing the numbers $7$ $7$ and $8$ $8$ . The quantities represented by them is compared in the figure. It is found that $7$ $7$ is smaller than $8$ $8$ .

Simplified Procedure -- Comparison by ordered-sequence: To find if one numbers is larger or smaller than another number, the numbers are compared using the order $0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, \dots$ $0,1,2,3,4,5,6,7,8,9, 10, 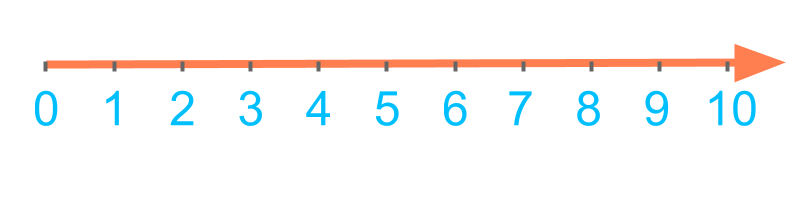cdots$ . comparing on number line Example: Comparing the numbers $4$ $4$ and $7$ .

$4$ is on the left-side to $7$ in the order $0,1,2,3,4,5,6,7,8,9$ and so $4$ is smaller than $7$ .

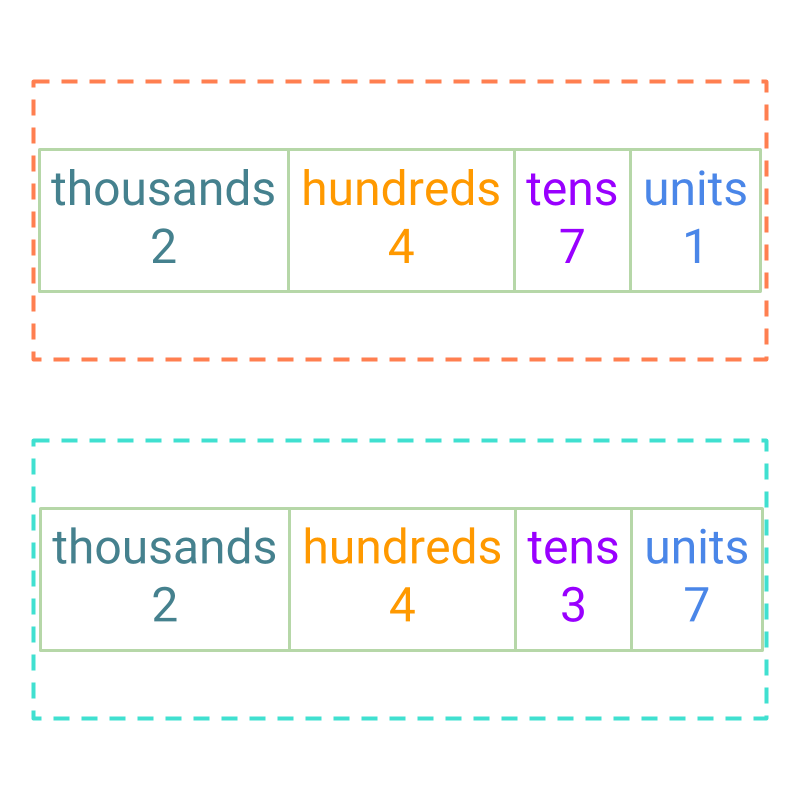
Comparison by Place-value -- Simplified Procedure to Compare Large Numbers: To find if one number is larger or smaller than another number, the digits at the highest place value are compared and if they are equal, then the digits at next lower place value are compared. comparing numbers simplified procedure

comparing given

Comparing two whole numbers $3$ and $6$ , it is found that $6>3$ .

In directed whole numbers, or, integers form, $6$ is $text(received:)3$ and $3$ is $text(received:)6$ . In integers too, $text(received:)3 > text(received:)6$ .

$3$ and $-6$ are compared.

The numbers are, $text(received:)3$ and $text(given:)6$ in directed whole number format.

$text(received:)3 > text(given:)6$

To understand how $text(received:)3$ is larger than $text(given:)6$ , consider the box-of-candy example.

A girl and her brother each have a box of candies. The number of candies in the box is not counted and they have equal numbers to start with.

She received $3$ candies.
Her brother gave $6$ candies.

Who would have more candies?
Obviously the sister as the number of candies in her box increased. The number of candies in brother's box decreased because he gave away some of the candies he had.

Consider the numbers $text(received:)3$ and $text(received:)6$ . $text(received:)6$ is larger than $text(received:)3$ . The comparison is in terms of amount received.

Consider the numbers $text(received:)3$ and $text(given:)6$ . In this, $text(given:)6$ gives a value opposite of amount received. When comparing in terms of amount received, $text(received:)3$ is larger than $text(given:)6$ .

This can be generalized to, negative numbers are smaller than positive numbers.

Comparing $-3$ and $-6$ .

comparison is in terms of amount received. and
$-3 = text(given:)3$
$-6 = text(given:)6$

In terms of amount received, $text(given:)3 > text(given:)6$

To understand how $text(given:)3$ is larger than $text(given:)6$ , consider the box-of-candy example.

A girl and her brother each have a box of candies. The number of candies in the box is not counted and they have equal numbers to start with.

She gave $3$ candies.
Her brother gave $6$ candies.

Who has more candies?
Sister has more candies. The number of candies in the sister's box is reduced a smaller amount. The number of candies in brother's box is reduced a larger amount.

When comparing in terms of amount received, $text(given:)3$ is larger than $text(given:)6$ ..

This can be generalized to the statement, negative number with larger absolute value is smaller than negative number with smaller absolute value.

Note the absolute values of the numbers are whole numbers and compared accordingly.

examples

Which of the following is smaller than the other? $21$ or $-26$
The answer is " $-26$ ." As per sign property of comparison, the negative number is smaller than the positive number.

Which of the following is smaller than the other? $-2183$ or $-2661$
The answer is " $-2661$ ". Both the numbers are negative. So, the larger amount in negative is smaller in values.

Comparing the numbers without the sign and using the comparison by place-value, 2 thousands equals 2 thousands. 6 hundreds is larger than 1 hundreds. So, 2661 is larger, and negative 2661 is smaller.

Which of the following is larger than the other? $-341$ or $-341$
The answer is "they are equal"

Which one is larger among $-23$ and $-156$ ?
The answer is " $-23$ ". Compare the absolute values $23$ and $156$ . The smaller absolute value is the larger number.

Find the smaller number among $-2323$ and $-99$ ?
The answer is " $-2323$ ". Compare the absolute values $2323$ and $99$ . The larger absolute value is the smaller number.

summary

Comparison of Integers -- First Principles: : Comparison is in terms of the amount received.

Amount given is smaller than amount received, as comparison is by amount received.

Larger amount given is smaller than smaller amount given, as comparison is by the amount received.

Comparison of Integers -- Simplified Procedure:

sign-property of comparison
• +ve and +ve are compared as whole numbers.
• When comparing +ve and -ve, the +ve value is larger irrespective of the absolute values of the numbers.
• When comparing -ve and -ve, the number with smaller absolute value is larger than the other.

The absolute values are compared as the simplified procedure detailed in whole numbers comparison by place-value.

Outline

The outline of material to learn integers is as follows.

Note: click here for detailed outline of Integers (directed numbers)

→ Introduction to Directed Numbers

→ Handling Direction

→ Ordinal Property

→ Sign and Absolute Value

→ Comparing Integers

→ Predecessor & Successor

→ Largest & Smallest

→ Ascending & Descending

→ Addition: First Principles

→ Addition: Simplified Procedure

→ Subtraction: First Principles

→ Subtraction: Simplified Procedure

→ Multiplication: First Principles

→ Multiplication: Simplified Procedure

→ Division: First Principles

→ Division: Simplfied Procedure

→ Numerical Expressions with Integers

→ PEMA / BOMA