Integers : Ordinal Property of Integers

maths > integers

Ordinal Property of Integers

what you'll learn...

overview

In whole numbers, we had studied that the numbers are in ordered sequence $0, 1, 2, \dots$ $0, 1, 2, cdots$ .

Where does the negative numbers fit in this?

Considering the following
$2 + (- 1) = 1$ $2+(-1) = 1$
$2 + (- 2) = 0$ $2+(-2) = 0$
$2 + (- 3) = - 1$ $2+(-3) = -1$
negative numbers are positioned to the left of $0$ $0$ .

$\dots, - 2, - 1, 0, 1, 2, \dots$ $cdots,-2, -1, 0, 1, 2, cdots$

ordered sequence

One of the fundamental properties of whole numbers is that, numbers are in an ordered sequence representing the magnitude of quantity represented by them.

The whole numbers are in the ordered sequence

$0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,$ etc. This is the ordinal property of whole numbers.

The word "ordinal" means: relating to order or series.

Ordinal property of whole numbers refers to the order 0, 1, 2, 3, et cetera.

order in negative

Integers are directed whole numbers, having positive and negative numbers.

Do integers have the ordinal property?

Are negative numbers ordered?

Where are the negative numbers placed in reference to the positive numbers?

To answer these questions, let us look at the properties in the number line.

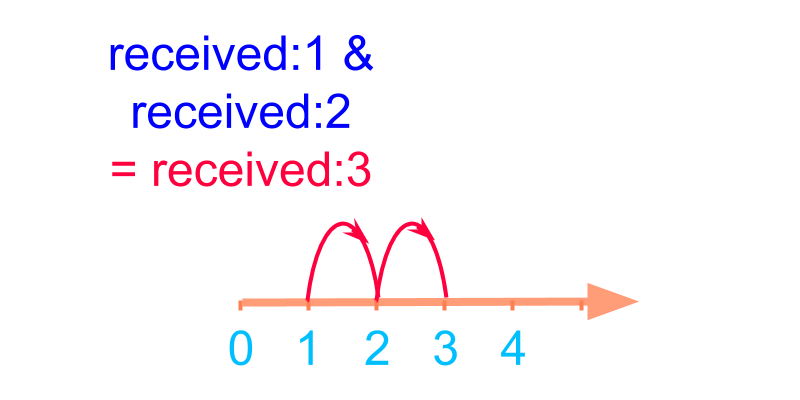
Consider combining the two numbers $text(received:)1$ and $text(received:)2$ .

The addition is shown in number-line in the figure. The sum is $3$ .The addition is shown in number-line in the figure.

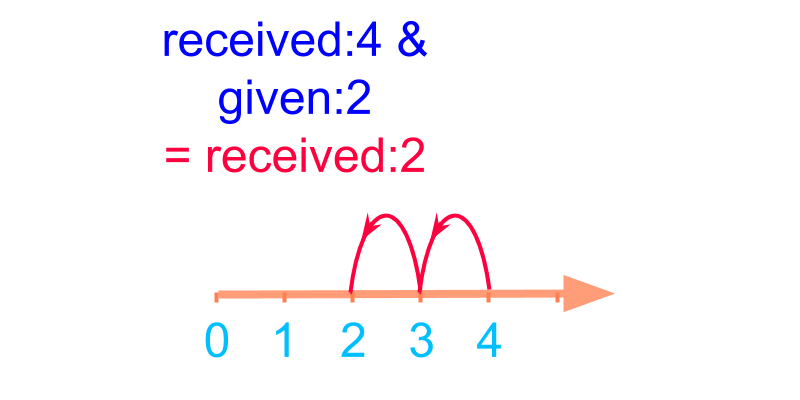
Consider combining the two numbers $text(received:)4$ and $text(given:)2$ . The sum is $2$ .

$4+(-2) = 2$
The addition is shown in number-line in the figure.

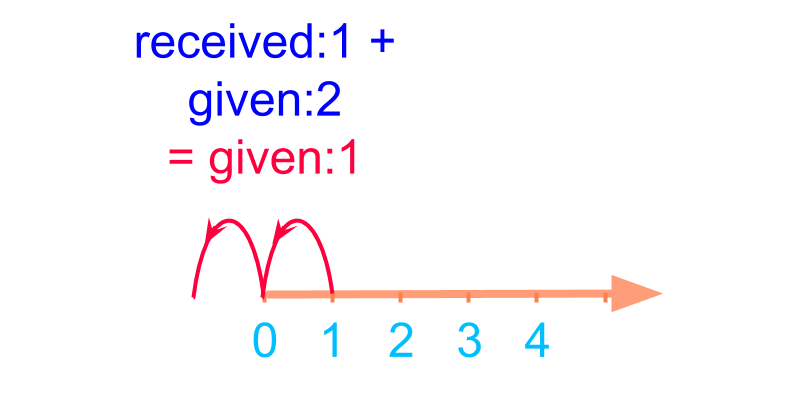
Consider combining the two numbers $text(received:)1$ and $text(given:)2$ .

The addition is shown in number-line in the figure.

$1+(-2)=-1$ .

In the number line the position of $-1$ is the position before the value $0$ . The addition is shown in number-line in the figure.

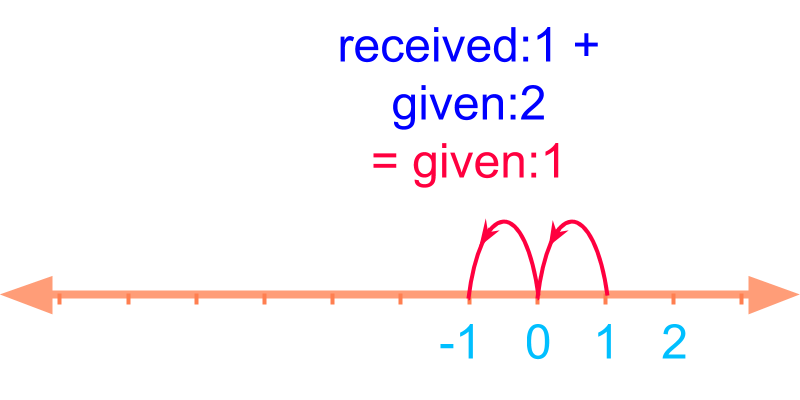
Consider combining the two $text(received:)1$ and $text(given:)2$ . This is $1+(-2)=-1$ and the position of the $-1$ is fixed to the left of $0$ .

The position of $-1$ is shown in the figure.

The whole number-line starts from $0$ and extends in positive direction.
The integer number-line extends in both the directions as shown.

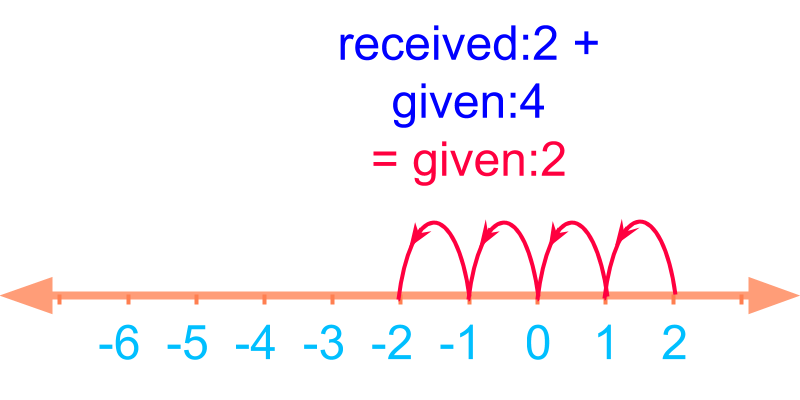
Consider combining the two numbers $text(received:)2$ and $text(given:)4$ .

The answer is $-2$

$2+(-4)=-2$ .

$-2$ is placed one position before $-1$ .

Extending the placement of $-1$ and $-2$ , the other negative numbers are placed as shown in the figure. The addition is shown in number-line in the figure.

summary

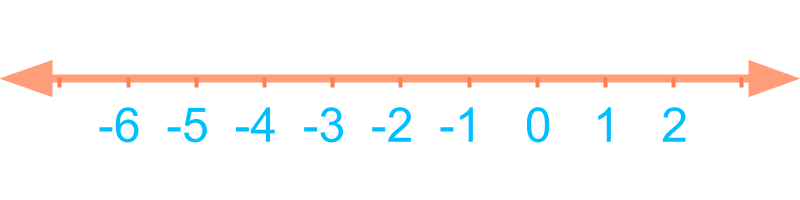
Ordered Sequence in Integers:
$cdots,-2, -1, 0, 1, 2, cdots$ .
The integer number line is shown in the figure.

Outline

The outline of material to learn integers is as follows.

Note: click here for detailed outline of Integers (directed numbers)

→ Introduction to Directed Numbers

→ Handling Direction

→ Ordinal Property

→ Sign and Absolute Value

→ Comparing Integers

→ Predecessor & Successor

→ Largest & Smallest

→ Ascending & Descending

→ Addition: First Principles

→ Addition: Simplified Procedure

→ Subtraction: First Principles

→ Subtraction: Simplified Procedure

→ Multiplication: First Principles

→ Multiplication: Simplified Procedure

→ Division: First Principles

→ Division: Simplfied Procedure

→ Numerical Expressions with Integers

→ PEMA / BOMA