Integers : Integer Subtraction : Simplified Procedure

maths > integers

Integer Subtraction : Simplified Procedure

what you'll learn...

overview

The subtraction in first principles was explained as taking away a quantity from another quantity and counting or measuring the remaining quantity.

For integers, the positive and negative numbers are to be handled appropriately. By considering all the combination of signs in subtrahends and minuends, a simplified procedure is derived.

Integer subtraction is handled as integer addition with addends (a) minuend and (b) the negative of subtrahend.

$minuend - subtrahend$ $text(minuend )-text( subtrahend )$
$= minuend as addend$ $= text( minuend as addend )$ $+ negative of subtrahend as addend$ $+ text( negative of subtrahend as addend)$

de-grouping

In whole numbers, we had studied the following.

Subtraction by Place-value with de-grouping -- Simplified Procedure : A number is subtracted from another as per the following procedure:

• the place-value positions are arranged units under units, $10$ $10$ s under $10$ $10$ s, etc.

• the units are subtracted and if the minuend digit is smaller than the subtrahend digit, then one ten's place is borrowed to make the minuend at the position larger. Then subtraction is carried out.

• continue to the higher place-value position. 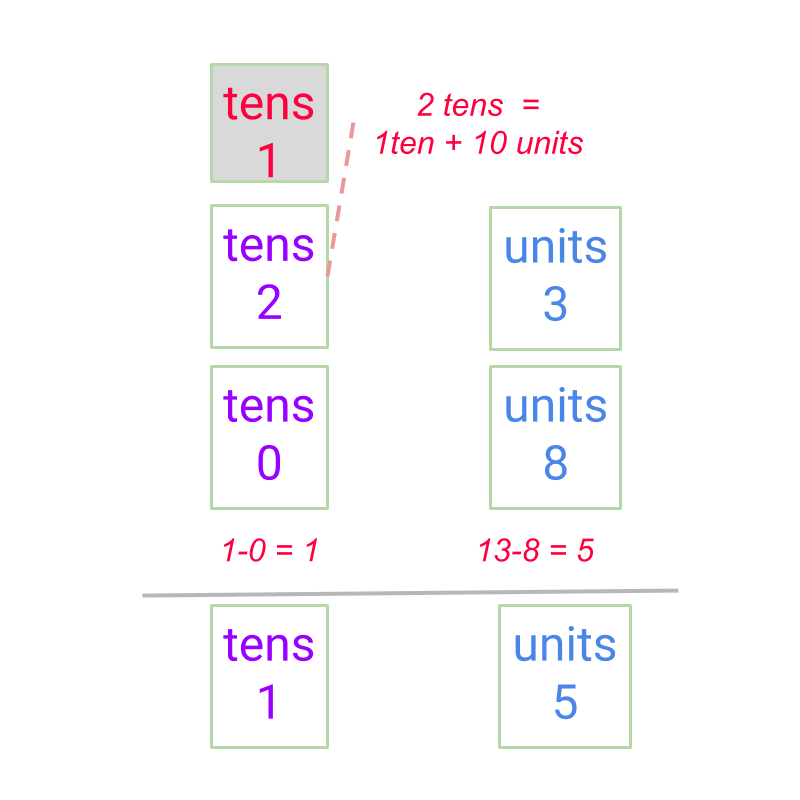subtraction meaning The "borrow" is the simplification of taking $1$ $1$ from a place value to $10$ $10$ pieces of a lower place value.

$4 - 3 = 1$ $4-3=1$

By first principles, $received: 4$ $text(received:)4$ minus $received: 3$ $text(received:)3$ equals $received: 1$ $text(received:)1$ .

This subtraction is equivalent to addition of integers $4 + (- 3) = 1$ $4+(-3) = 1$ .

$4 - (- 3) = 7$ $4-(-3) = 7$

By first principles, $received: 4$ $text(received:)4$ minus $given: 3$ $text(given:)3$ equals $received: 7$ $text(received:)7$ .

This subtraction is equivalent to addition of integers $4 + (+ 3) = 7$ $4+(+3) = 7$ .

$- 4 - (- 3) = - 1$ $-4 - (-3) = -1$

By first principles, $given: 4$ $text(given:)4$ minus $given: 3$ $text(given:)3$ equals $given: 1$ $text(given:)1$ .

This subtraction is equivalent to addition of integers $- 4 + (+ 3) = - 1$ $-4 + (+3) = -1$ .

$- 4 - (- 5) = 1$ $-4 - (-5) = 1$

By first principles, $given: 4$ $text(given:)4$ minus $given: 5$ $text(given:)5$ equals $received: 1$ $text(received:)1$ .

This subtraction is equivalent to addition of integers $- 4 + (+ 5) = 1$ $-4 + (+5) = 1$ .

Note the following

• $4 - 3 = 4 + (- 3) = 1$ $4 - 3 = 4 + (-3) = 1$

• $4 - (- 3) = 4 + (+ 3) = 7$ $4-(-3) = 4 + (+3) =7$

• $- 4 - (- 3) = - 4 + (+ 3) = - 1$ $-4-(-3) = -4 + (+3) = -1$

• $- 4 - (- 5) = - 4 + (+ 5) = 1$ $-4-(-5) = -4 + (+5) = 1$

Based on this, the subtraction is simplified and handed as addition of negative of subtrahend. That is,

$minuend - subtrahend$ $text(minuend ) - text( subtrahend )$ $= minuend + (- subtrahend)$ $= text(minuend ) + (-text(subtrahend))$

Integer Subtraction Simplified Procedure : Sign-Property of Integer Subtraction:

Integer subtraction is handled as integer addition with addends
(a) minuend and
(b) the negative of subtrahend.

$minuend - subtrahend$ $text(minuend )-text( subtrahend )$
$= minuend as addend$ $= text( minuend as addend )$ $+ negative of subtrahend as addend$ $+ text( negative of subtrahend as addend)$

examples

Find the result of $(- 6) - 0$ $(-6)-0$ .
The answer is " $- 6$ $-6$ "

Find the result of $- 140$ $-140$ subtracted from $11$ $11$ .
The answer is " $151$ $151$ "

Find the result of $2$ $2$ subtracted from $- 2$ $-2$
The answer is " $- 4$ $-4$ "

Find the result of $- 2345$ $-2345$ subtracted from $- 889$ $-889$
The answer is " $1456$ $1456$ "

summary

Sign-Property of Integer Subtraction:

Integer subtraction is handled as integer addition with addends (a) minuend and (b) the negative of subtrahend.

$minuend - subtrahend$ $text(minuend )-text( subtrahend )$
$= minuend as addend$ $= text( minuend as addend )$ $+ negative of subtrahend as addend$ $+ text( negative of subtrahend as addend)$

Outline

The outline of material to learn integers is as follows.

Note: click here for detailed outline of Integers (directed numbers)

→ Introduction to Directed Numbers

→ Handling Direction

→ Ordinal Property

→ Sign and Absolute Value

→ Comparing Integers

→ Predecessor & Successor

→ Largest & Smallest

→ Ascending & Descending

→ Addition: First Principles

→ Addition: Simplified Procedure

→ Subtraction: First Principles

→ Subtraction: Simplified Procedure

→ Multiplication: First Principles

→ Multiplication: Simplified Procedure

→ Division: First Principles

→ Division: Simplfied Procedure

→ Numerical Expressions with Integers

→ PEMA / BOMA