Complex Numbers : Properties of Complex Addition

maths > complex-number

Properties of Complex Addition

what you'll learn...

Overview

Understanding Properties of Complex Arithmetic
» The properties of real number arithmetic is extended to include $i = \sqrt{- 1}$ $i=sqrt(-1)$ as a number that cannot be added or multiplied to other real-numbers.Properties of Complex numbers extend on properties of Real numbers.

» Complex Addition is closed.
    → $z_{1} + z_{2} \in ℂ$ $z_1 + z_2 in CC$

» Complex Addition is commutative.
    → $z_{1} + z_{2} = z_{2} + z_{1}$ $z_1 + z_2 = z_2 + z_1$

» Complex Addition is associative.
    → $z_{1} + (z_{2} + z_{3}) = (z_{1} + z_{2}) + z_{3}$ $z_1 + (z_2 +z_3) = (z_1+z_2)+z_3$

» Complex Additive identity is $0$ $0$ .
    → $z_{1} + 0 = z_{1}$ $z_1 + 0 = z_1$

» Complex Additive inverse of $z$ $z$ is $- z$ $-z$
    → $z_{1} + (- z_{1}) = 0$ $z_1 + (-z_1) = 0$

» Complex modulus of sum is less than or equal to sum of moduluses
    → $| z_{1} + z_{2} | \leq | z_{1} | + | z_{2} |$ $|z_1 + z_2| <= |z_1| + |z_2|$

Understanding Properties of Complex Arithmetic

complex number system is :

• Real number system extended to include solutions to polynomials.

• Real number system added with an additional number $\sqrt{- 1}$ $sqrt(-1)$

• Model of amplitude and phase of sine waves and elements interacting with sine waves

To understand properties of the complex numbers, the following are to be learned
• Properties of addition and subtraction
• Properties of multiplication and division
• Properties of exponents and roots
• properties like commutative, distributive, associative, etc.

One Need not learn each of these afresh. Instead, just extend the definitions and properties of real numbers as though complex number is a numerical expression.

Complex number is a numerical expression with $\sqrt{- 1}$ $sqrt(-1)$ as an element. When learning rules and properties of complex number, visualize the complex number as a numerical expression of real numbers.

summary

Complex Arithmetic Fundamentals: The properties of real number arithmetic is extended to include $\sqrt{- 1}$ $sqrt(-1)$ as a number that cannot be added or multiplied to other numbers.

Complex arithmetic is an extension of Real numbers arithmetic.

closure law

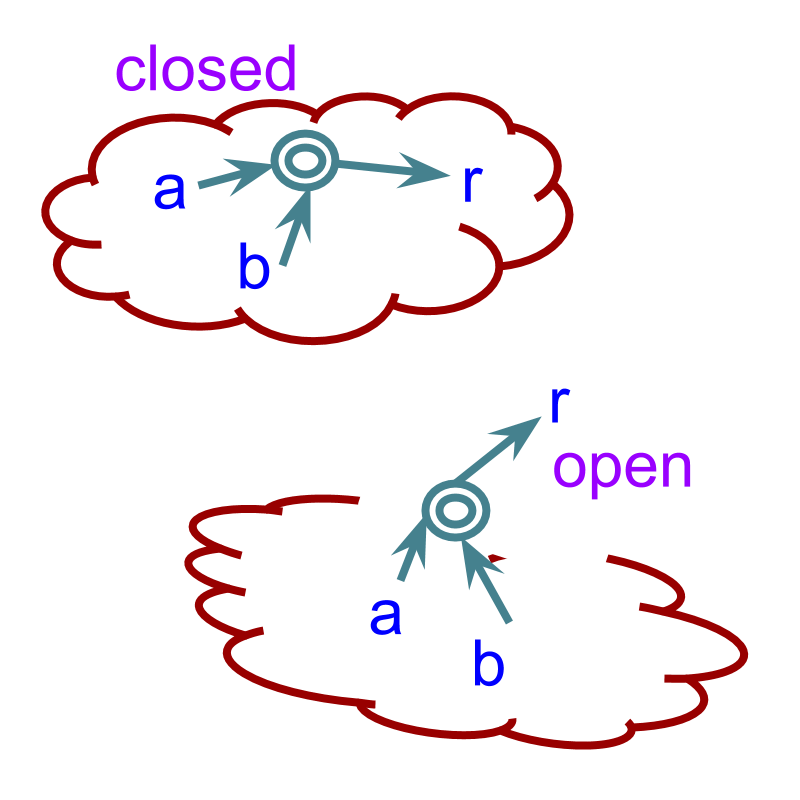
The word 'closure' means, closed and not open

The word "span" means "Full extent of something"

The span of complex numbers is
$a + i b$ $a+ib$ with $a, b \in ℝ$ $a,b in RR$

That is, real and imaginary parts taking any real number.

The span of complex numbers or the set of complex numbers is represented as $ℂ$ $CC$ .

When any two complex numbers are added, the result is another complex number.

summary

Closure Property of Addition and Subtraction: For any given complex numbers $z_{1}, z_{2} \in ℂ$ $z_1, z_2 in CC$ , $z_{1} \pm z_{2} \in ℂ$ $z_1 +- z_2 in CC$ .

Sum or difference of two complex numbers is another complex number - closure property

commutative law

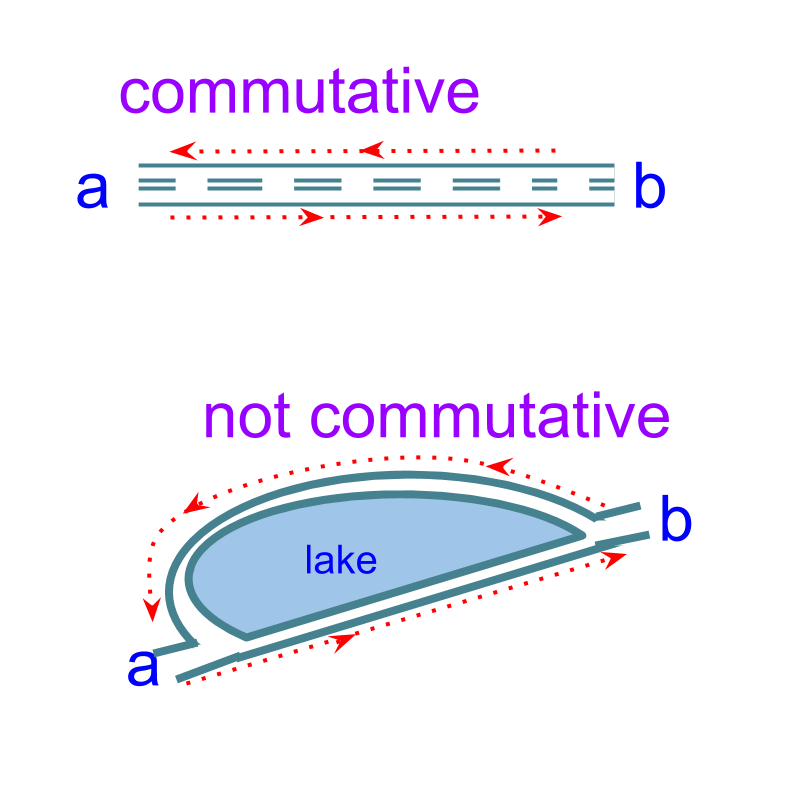
The word 'commute' means 'to go to and fro between two places on a regular basis'.

Consider the addition and subtraction of complex numbers. $z_{3} = z_{1} + z_{2}$ $z_3 = z_1+z_2$ given as $a_{3} + i b_{3} = (a_{1} + a_{2}) + i (b_{1} + b_{2})$ $a_3+ib_3 = (a_1+a_2)+i(b_1+b_2)$ , where $a_{1}, a_{2}, b_{1}, b_{2} \in ℝ$ $a_1, a_2, b_1, b_2 in RR$ .
$z_{4} = z_{2} + z_{1}$ $z_4 = z_2+z_1$ , and $a_{4} + i b_{4} = (a_{2} + a_{1}) + i (b_{2} + b_{1})$ $a_4+ib_4 = (a_2+a_1)+i(b_2+b_1)$

Since the real numbers are commutative, $a_{1} + a_{2} = a_{2} + a_{1}$ $a_1+a_2=a_2+a_1$ , and similarly for imaginary part. This proves that $z_{1} + z_{2} = z_{2} + z_{1}$ $z_1+z_2 = z_2+z_1$

The commutative property is not defined for real subtraction, and so not for complex subtraction.

Subtraction is the inverse of addition.

The commutative property has to be used in the following way.
$z_{1} - z_{2}$ $z_1-z_2$
$= z_{1} + (- z_{2})$ $quad quad = z_1 + (-z_2)$
$= (- z_{2}) + z_{1}$ $quad quad =(-z_2) + z_1$ (commutative property of addition.)

Given two complex numbers $z_{1}, z_{2}$ $z_1, z_2$ ; $z_{1} + z_{2} = 3.1 + i 2.9$ $z_1+z_2 = 3.1+i2.9$ . Find the value of $z_{2} + z_{1}$ $z_2+z_1$ .
The answer is ' $3.1 + i 2.9$ $3.1+i2.9$ '

summary

Commutative Property of Complex addition: for any complex number $z_{1}, z_{2} \in ℂ$ $z_1, z_2 in CC$
$z_{1} + z_{2} = z_{2} + z_{1}$ $z_1 + z_2 = z_2 + z_1$

Complex numbers can be swapped in complex addition - commutative.

Associative Law

The word 'Associate' means 'to connect with; to join'.

When three complex numbers are added,
• Person A associates the middle complex number with first complex number and, to the result of that, he adds the third complex number $(z_{1} + z_{2}) + z_{3}$ $(z_1 + z_2) + z_3$
• Person B associates the middle complex number with third complex number and to that she adds the first complex number $z_{1} + (z_{2} + z_{3})$ $z_1 + (z_2+z_3)$

If the real and imaginary parts of the numbers are substituted, and associative property of real numbers is applied, it is proven that $(z_{1} + z_{2}) + z_{3}$ $(z_1 + z_2) + z_3$ $= z_{1} + (z_{2} + z_{3})$ $=z_1 + (z_2+z_3)$

Associative property is not applicable to subtraction, but the property can be used as when subtraction is handled as inverse of addition. For $(z_{1} - z_{2}) - z_{3}$ $(z_1 - z_2) - z_3$ , it will be considered as $(z_{1} + (- z_{2})) + (- z_{3})$ $(z_1 + (-z_2)) + (-z_3)$ .

Given $z_{1}, z_{2} \in ℂ$ $z_1, z_2 in CC$ , what will be the result of $z_{1} + z_{2} + z_{1}$ $z_1 + z_2 + z_1$ ?

The answer is ' $2 z_{1} + z_{2}$ $2z_1+z_2$ '. This algebraic modification uses associative property of addition.

summary

Associative Property of Complex Addition: For Any complex number $z_{1}, z_{2}, z_{3} \in ℂ$ $z_1,z_2,z_3 in CC$ ,
$z_{1} + (z_{2} + z_{3}) = (z_{1} + z_{2}) + z_{3}$ $z_1+(z_2+z_3) = (z_1+z_2)+z_3$

Order of addition can be changed - associative.

additive identity

The word "identical" means "exactly alike; same in every detail"

Consider the complex number $0 + i 0$ $0+i0$ . The result of adding that with a complex number $z_{1}$ $z_1$ gives result as ' $z_{1}$ $z_1$ '. The sum is identical to the complex number being added.

An additive identity is 'an element, when added, will result in sum identical to the addend.'.

Consider $z_{1} = e + π i$ $z_1 = e+ pi i$ . What will be the sum $z_{1} + 0$ $z_1 + 0$ ?

The answer is ' $z_{1} + 0 = z_{1} = e + π i$ $z_1 + 0 = z_1 = e+ pi i$ '

summary

Additive Identity in complex numbers: For any complex number $z_{1} \in ℂ$ $z_1 in CC$ , there exists $0 = 0 + i 0, 0 \in ℂ$ $0 = 0+i0, 0 in CC$ such that
$z_{1} + 0 = z_{1}$ $z_1 + 0 = z_1$

$0 = 0 + i 0$ $0 = 0+i0$ is additive identity.

additive inverse

The word 'inverse' means 'opposite; converse'.

Consider two complex numbers $z_{1} = a + i b$ $z_1 = a+ i b$ and $z_{2} = - a - i b$ $z_2 = -a-ib$ .

$z_{1} + z_{2}$ $z_1+z_2$
$= a + i b - a - i b$ $= a+ib -a - ib$
$= a - a + i (b - b)$ $= a-a+ i (b-b)$
$= 0 + 0 i$ $= 0+0i$
$= 0$ $= 0$
$=$ $=$ additive identity

$- z$ $-z$ is called the additive inverse for $z$ $z$ as $z + (- z) = 0$ $z+(-z) = 0$ .

What is the additive inverse of $3.5 + 2.1 i$ $3.5+2.1i$ ?

The answer is ' $- 3.5 - 2.1 i$ $-3.5-2.1i$ '

summary

Additive Inverse: For any complex number $z = a + i b \in ℂ$ $z = a+ib in CC$ , there exists $- z = - a - i b \in ℂ$ $-z = -a - i b in CC$ such that
$z + (- z) = 0$ $z + (-z) = 0$

For any complex number $z$ $z$ there exits $- z$ $-z$ : additive inverse.

Modulus in addition

Given $z_{1} = a_{1} + i b_{1}$ $z_1 = a_1+ib_1$ and $z_{2} = a_{2} + i b_{2}$ $z_2 = a_2+ib_2$ , the modulus of sum $| z_{1} + z_{2} |$ $|z_1 + z_2|$ is ' $\leq | z_{1} | + | z_{2} |$ $<=|z_1| + |z_2|$ '.

$| z_{1} + z_{2} | \leq | z_{1} | + | z_{2} |$ $|z_1 + z_2| <= |z_1| + |z_2|$ is proven with the representation on complex plane. $z_{1}, z_{2}, z_{1} + z_{2}$ $z_1, z_2, z_1+z_2$ form a triangle. Length of the sides of the triangle are $| z_{1} |, | z_{2} |, | z_{1} + z_{2} |$ $|z_1|, |z_2|, |z_1+z_2|$ . Sum of any two sides of the triangle is greater than the third side.

Given $z_{1} = a_{1} + i b_{1}$ $z_1 = a_1+ib_1$ and $z_{2} = a_{2} + i b_{2}$ $z_2 = a_2+ib_2$ what is the modulus of difference $| z_{1} - z_{2} |$ $|z_1 - z_2|$ ?

The answer is ' $\leq | z_{1} | + | z_{2} |$ $<=|z_1| + |z_2|$ '. Subtraction is the inverse of addition. So, $| z_{1} - z_{2} |$ $|z_1 - z_2|$ = $| z_{1} + (- z_{2}) |$ $|z_1 + (-z_2)|$ . $\leq | z_{1} | + | - z_{2} |$ $<= |z_1|+|-z_2|$ $\leq | z_{1} | + | z_{2} |$ $<= |z_1| + |z_2|$ . Note : $| - z_{2} | = | z_{2} |$ $|-z_2| = |z_2|$

summary

Modulus of Sum: For complex numbers $z_{1}, z_{2} \in ℂ$ $z_1, z_2 in CC$
$| z_{1} + z_{2} | \leq | z_{1} | + | z_{2} |$ $|z_1 + z_2| <= |z_1| + |z_2|$

Modulus of sum is less than or equal to the sum of modulus.

Outline

The outline of material to learn "complex numbers" is as follows.

Note : Click here for detailed overview of Complex-Numbers

→ Complex Numbers in Number System

→ Representation of Complex Number (incomplete)

→ Euler's Formula

→ Generic Form of Complex Numbers

→ Argand Plane & Polar form

→ Complex Number Arithmetic Applications

→ Understanding Complex Artithmetics

→ Addition & Subtraction

→ Multiplication, Conjugate, & Division

→ Exponents & Roots

→ Properties of Addition

→ Properties of Multiplication

→ Properties of Conjugate

→ Algebraic Identities