Complex Numbers

maths

Complex Numbers

Welcome to the novel approach to understanding complex numbers: it completely changes the way complex numbers are thought-about and learned.

• Irrational numbers are numerical expressions, eg: $2 + \sqrt[5]{3}$ $2+root(5)(3)$

» Complex numbers are numerical expressions too.

• Irrational numbers do not have a standard form. They are expressed as numerical expressions, with some having many terms. eg: $2 + \sqrt[2]{2} - 3 \times \sqrt[3]{5}$ $2+ root(2)(2)-3xx root(3)(5)$

» Similar to irrational numbers, the direct extension is to express complex numbers as numerical expressions. eg: $x^{3} = 1$ $x^3=1$ has $3$ $3$ solutions, ${(\sqrt[3]{1})}_{1 s t}$ $(root(3)(1))_(1st)$ , ${(\sqrt[3]{1})}_{2 n d}$ $(root(3)(1))_(2nd)$ , ${(\sqrt[3]{1})}_{3 r d}$ $(root(3)(1))_(3rd)$

» But, Any complex number is given in a standard form $a + i b$ $a+ib$ , because of Euler Formula $r e^{i θ}$ $re^(i theta)$ $= r (\cos θ + i \sin θ)$ $= r(cos theta + i sin theta)$

How so? Go through the first few lessons to get the astoundingly new perspective of complex numbers.

maths > complex-number > complex-number-in-number-system

Complex Numbers in Number System

This page starts with a quick revision of number system hierarchy. Complex numbers are introduced as an extension of Real Numbers. Then it reviews, the representation of irrational numbers. The complex number notation is very similar to the representation of irrational numbers -- both are given as numerical expressions.

Number System Hierarchy

» Natural or counting numbers
    → Counting with hands 1, 2, 3, ...

» whole numbers
    → 0 is included

» integers
    → negatives are included.

» rational numbers
    → fractions and decimals are included.

» real numbers
    → irrational numbers included. numbers represented as expressions

» complex number : $a + i b$ $a+ib$ form
    → $a$ $a$ is the real part
    → $b$ $b$ is the imaginary part
    → $i = \sqrt{- 1}$ $i = sqrt(-1)$
    → Complex means "consisting of many different parts"

Irrational Number Representation

» irrational numbers
    → solutions of algebraic equations in real line
    → eg: $\sqrt{2}$ $sqrt(2)$ is one solution of $x^{2} = 2$ $x^2=2$

» irrational numbers are represented as numerical expressions
    → eg: $3 + 4 \sqrt[3]{5}$ $3+4 root(3)(5)$ is one solution of ${(\frac{x - 3}{4})}^{3} = 5$ $((x-3)/4)^3 = 5$

maths > complex-number > complex-number-incomplete-notation

Representation of Complex Numbers (incomplete)

In this page, as initial understanding of complex numbers, quadratic equations are examined. The solutions to quadratic equations is in the form $a + i b$ $a+ib$ , where $i = \sqrt{- 1}$ $i=sqrt(-1)$ . Complex number in the form $a + i b$ $a+ib$ can be equivalently represented in the form $r (\cos θ + i \sin θ)$ $r(cos theta + i sin theta)$ . This representation, has an advantage to understanding the generic form of complex numbers.

Complex number Representation

» Abstraction of complex numbers
    → solution of algebraic equations in 2D plane
    → eg: $x^{3} = 1$ $x^3=1$ has $3$ $3$ solutions, ${(\sqrt[3]{1})}_{1 s t}$ $(root(3)(1))_(1st)$ , ${(\sqrt[3]{1})}_{2 n d}$ $(root(3)(1))_(2nd)$ , ${(\sqrt[3]{1})}_{3 r d}$ $(root(3)(1))_(3rd)$

» complex numbers are numerical expressions
    → eg: $3 + 4 \sqrt[4]{- 5}$ $3+4 root(4)(-5)$ is one solution to ${(\frac{x - 3}{4})}^{4} = - 5$ $((x-3)/4)^4 = -5$

» solution to quadratic equation in the form $a + i b$ $a+ib$
    → $i = \sqrt{- 1}$ $i=sqrt(-1)$

Note: irrational numbers do not have a generic form. But, it is later proven that all complex numbers can be expressed in the form $a + i b$ $a+ib$ .

For now, only solution to quadratic equation is shown to be in the form $a + i b$ $a+ib$ .

Representations of Complex Numbers

» coordinate form $a + i b$ $a+ib$

» polar form $r (\cos θ + i \sin θ)$ $r(cos theta + i sin theta)$
abstracted from $a + i b$ $a+ib$
    → $r = \sqrt{a^{2} + b^{2}}$ $r=sqrt(a^2+b^2)$
    → $\cos θ = \frac{a}{r}$ $cos theta = a/r$
    → $\sin θ = \frac{b}{r}$ $sin theta = b/r$

maths > complex-number > complex-number-euler-formula

Euler's Formula

To understand the generic form of complex numbers as $a + i b$ $a+i b$ , one should know Euler's Formula. This helps to convert numerical expressions of various forms to the form $a + i b$ $a+i b$ .

Euler's formula

» exponent form of complex number

» $r e^{i θ}$ $re^(i theta)$ $= r (\cos θ + i \sin θ)$ $= r(cos theta + i sin theta)$
→ $e$ $e$ is the base of natural logarithm
→ abstracted based on the properties of polar form $r (\cos θ + i \sin θ)$ $r(cos theta + i sin theta)$ The coordinate form, polar form, and exponent form help to establish a generic representation $a + i b$ $a+ib$ for all complex numbers.

maths > complex-number > generic-form-complex-numbers

Generic Form of Complex Numbers

Irrational numbers are specified with the operations such as $+$ $+$ , $\sqrt{}$ $sqrt( )$ , $\sqrt[5]{}$ $root(5)( )$ etc. Unlike irrational numbers, complex numbers have an uniform representation. This page explains this in detail.

Generic Form of Complex Numbers

» All complex numbers are in the form $a + i b$ $a+ib$

» Example: Solutions of $x^{3} = - 1$ $x^3=-1$

→ ${(\sqrt[3]{- 1})}_{1 s t} = e^{\frac{i π}{3}}$ $(root(3)(-1))_(1st) =e^((i pi)/3)$ $= \frac{1}{2} + i \frac{\sqrt{3}}{2}$ $= 1/2 + i sqrt(3)/2$

→ ${(\sqrt[3]{- 1})}_{2 n d} = e^{i π}$ $(root(3)(-1))_(2nd) =e^(i pi)$ $= - 1$ $= -1$

→ ${(\sqrt[3]{- 1})}_{3 r d} = e^{\frac{i 5 π}{3}}$ $(root(3)(-1))_(3rd) =e^((i 5pi)/3)$ $= \frac{1}{2} - i \frac{\sqrt{3}}{2}$ $= 1/2 - i sqrt(3)/2$

maths > complex-number > complex-number-polar-form

Argand Plane and Polar Form

Complex number $a + i b$ $a+i b$ is equivalently an ordered pair $(a, b)$ $(a,b)$ which can be abstracted to represent a 2D plane called Argand Plane or Complex Plane.

Complex Plane

» Real line extended to complex plane
    → Argand Plane 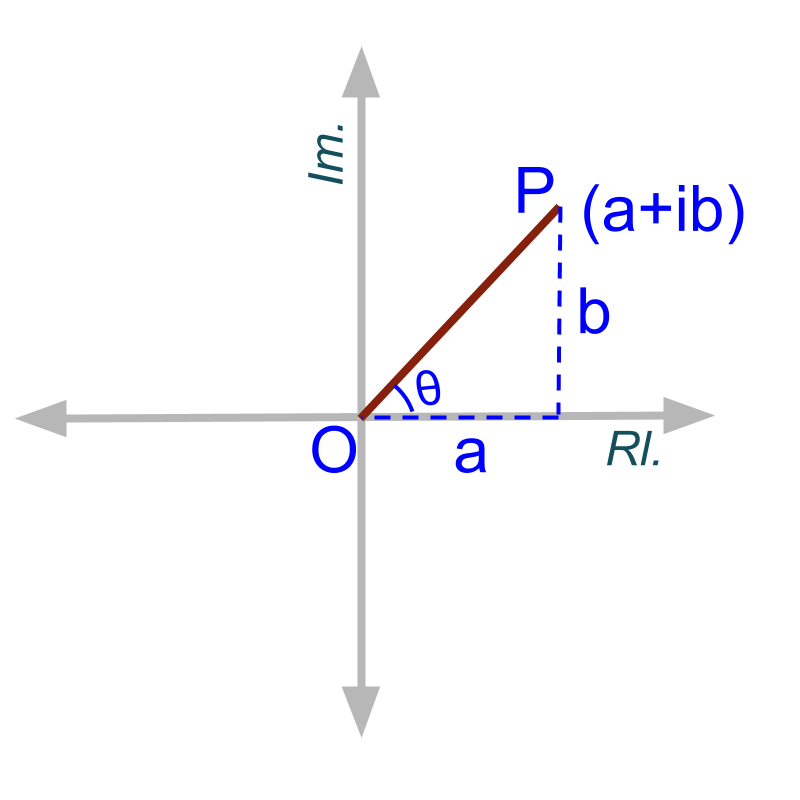» Complex plane for $a + i b$ $a+ib$

    → real part $a$ $a$ on real-axis or real-line

    → imaginary part $b$ $b$ on imaginary-axis

    → coordinate equivalent $(a, b)$ $(a,b)$

Modulus

» distance from origin $(0, 0)$ $(0,0)$ is modulus $r$ $r$ » $| a + i b |$ $|a+ib|$ $= r = \sqrt{a^{2} + b^{2}}$ $= r = sqrt(a^2+b^2)$
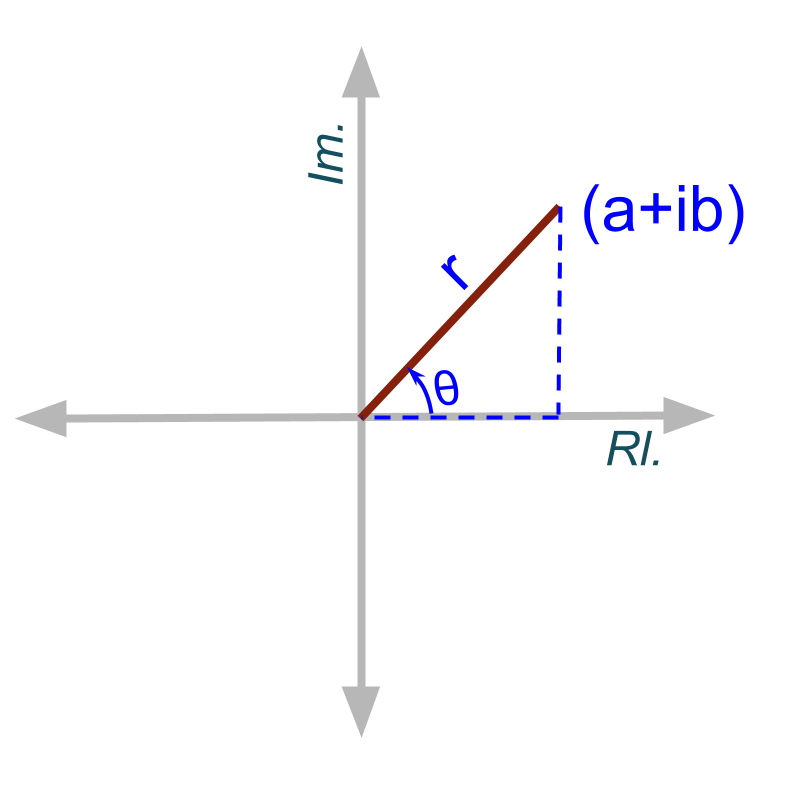by Pythagorean Theorem

Argument

» Angle with positive real-axis » $θ = \tan^{- 1} (\frac{b}{a})$ $theta = tan^(-1) (b/a)$

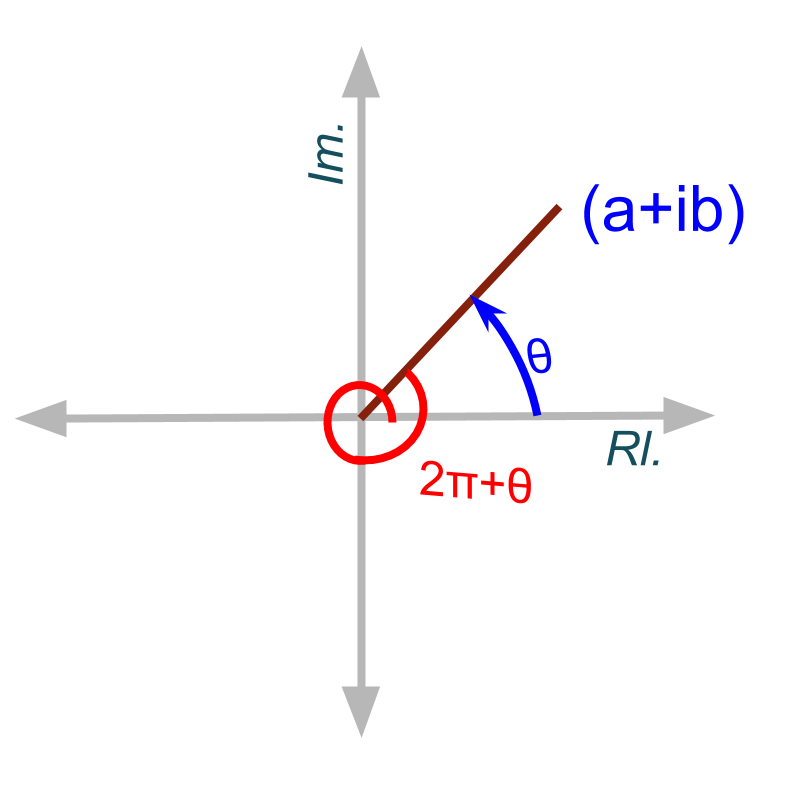» Arguments $= 2 n π + θ$ $= 2npi+theta$ where $n = 0, 1, 2, ...$ $n=0,1,2,...$

» Principal argument $= θ$ $= theta$ where $0 \leq θ < 2 π$ $0 <= theta < 2pi$

Polar form

$a + i b$ $a+ib$ $= r (\cos θ + i \sin θ)$ $=r(cos theta+i sin theta)$ $= r e^{i θ}$ $=re^(itheta)$

maths > complex-number > modeling-sine-waves-complex-arithmetic

Complex Number Arithmetics & modeling sine waves

This page brings up the question, what are the applications of complex numbers and outlines those application scenarios. This page provides proofs, illustration, and explanation to how complex number is used to model sine waves and elements interacting with sine waves.

Basis of Complex Number Arithmetic

» Modeling sine waves
    → same frequency $ω$ $omega$

    → different amplitude $r$ $r$

    → different phase $ϕ$ $phi$ » amplitude and phase

    → $\sin 1.1 x$ $sin1.1x$ is shown in blue

    → $2.5 \sin (1.1 x + 0.7)$ $2.5sin(1.1x+0.7)$ is shown in orange
$2.5$ $2.5$ amplitude is the size change.
$0.7$ $0.7$ phase is the horizontal shift.

Modeling sine waves

» Algebraic explanation
    → $r \sin (ω x + ϕ)$ $r sin(omega x + phi)$

substitute $\sin (A + B)$ $sin(A+B)$ formula
    → $= r (\cos ϕ \sin ω x$ $= r(cos phi sin omega x$ $+ \sin ϕ \cos ω x)$ $+ sin phi cos omega x)$

substitute $\cos ω x = i \sin ω x$ $cos omega x = i sin omega x$
    → $= r (\cos ϕ + i \sin ϕ) \sin ω x$ $= r(cos phi + i sin phi)sin omega x$

substitute coordinate form of complex number
    → $= (a + i b) \sin ω x$ $=(a+ib)sin omega x$

considering that $ω$ $omega$ is a constant, $\sin ω x$ $sin omega x$ can be taken off the expression.
    → $= a + i b$ $=a+ib$

» Geometrical explanation
    → $r \sin (ω x + ϕ)$ $r sin(omega x + phi)$
A sine wave with an amplitude and phase can be equivalently represented as sum of a sine wave and a cosine wave of different amplitudes and $0$ $0$ phase.       $2.5 \sin (1.1 x + .7)$ $2.5 sin(1.1x+.7)$
      $= 2.5 \cos (.7) \sin (1.1 x)$ $= 2.5 cos(.7)sin(1.1x)$
      $+ 2.5 \sin (0.7) \cos (1.1 x)$ $+ 2.5 sin(0.7)cos(1.1x)$

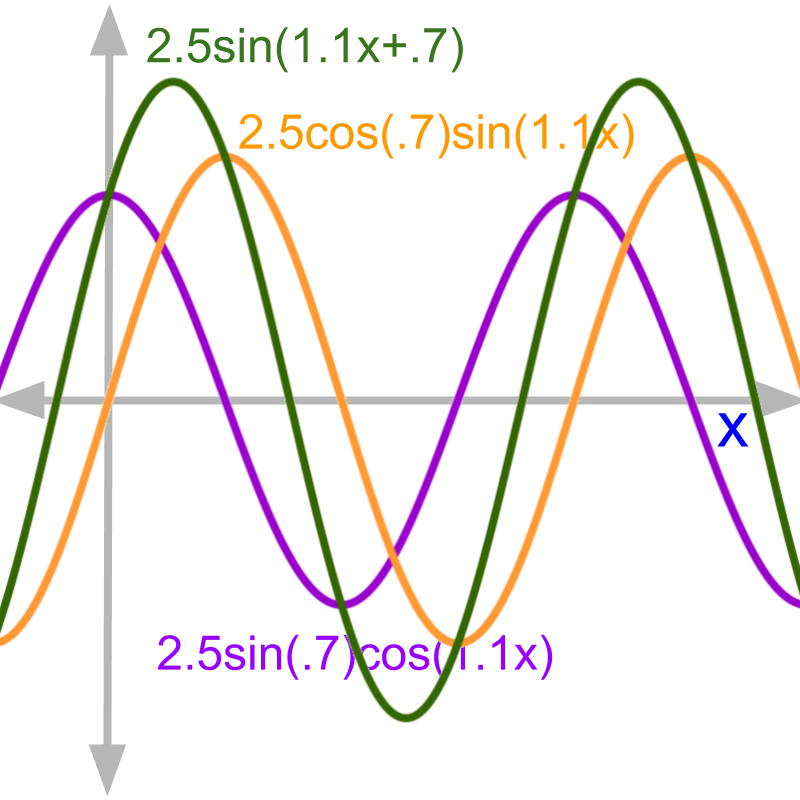
» Sine waves of same frequency is modeled with complex number $a + i b$ $a+ib$
    → Complex addition as per sine wave addition
    → Complex multiplication as per sine wave interaction.

maths > complex-number > understanding-complex-arithmetic-and-equivalence

Understanding Complex Arithmetic and equivalence

Complex number arithmetic like addition, multiplication, etc are nothing but extension of real number arithmetic. Complex Arithmetic as Numerical Expression

» Real Number arithmetic

    → Addition with closure, commutative, associative, identity, inverse properties

    → Multiplication with closure, commutative, associative, distributive, identity, inverse properties

    → subtraction and division as inverse of addition and multiplication respectively

    → PEMDAS / BODMAS Precedence rule

» Complex number arithmetic
    → extension of real arithmetic with additional number $i$ $i$
    → $i$ $i$ is handled like a variable
    → $i^{2} = - 1$ $i^2 = -1$ maps $i$ $i$ to a real number

When Two Complex numbers are Equal?

» if two complex numbers $a + i b$ $a+ib$ and $c + i d$ $c+id$ are equal then

    → $a = c$ $a=c$ and

    → $b = d$ $b=d$

maths > complex-number > complex-number-addition-subtraction

Addition and Subtraction of Complex numbers

Complex Number Addition

» $(a + i b) + (c + i d)$ $(a+ib) + (c+id)$
by associative, commutative, distributive laws of real numbers and by considering $i$ $i$ as a variable
→ $= (a + c) + i (b + d)$ $=(a+c) + i(b+d)$

Complex Number Subtraction

» $(a + i b) - (c + i d)$ $(a+ib) - (c+id)$
by associative, commutative, distributive laws of real numbers and by considering $i$ $i$ as a variable
→ $= (a - c) + i (b - d)$ $=(a-c) + i(b-d)$

maths > complex-number > complex-number-multiplication-conjugate-division

Multiplication, Conjugate, & Division in Complex numbers

Complex number multiplication

» $(a + i b) \times (c + i d)$ $(a+ib) xx (c+id)$
by associative, commutative, distributive laws of real numbers, considering $i$ $i$ as a variable, and applying $i^{2} = - 1$ $i^2=-1$
    → $= (a c - b d) + i (c b + a d)$ $=(ac-bd) + i(cb+ad)$

Complex Number Conjugate

» Conjuage of $a + i b$ $a+ib$
Conjugate means "coupled or related". Conjugate of a complex number makes the number real by addition or multiplication.

    → $= \bar{a + i b}$ $=bar(a+ib)$
    → $= a - i b$ $=a-ib$

Complex Number Division

» $(a + i b) \div (c + i d)$ $(a+ib) -: (c+id)$
by multiplicative identity, multiplicative inverse, distributive properties.

    → $= \frac{a + i b}{c + i d}$ $= (a+ib)/(c+id)$ $\times \frac{c - i d}{c - i d}$ $xx (c-id)/(c-id)$

    → $= \frac{(a + i b) \times (c - i d)}{c^{2} + d^{2}}$ $= ((a+ib)xx(c-id)) / (c^2+d^2)$

maths > complex-number > complex-number-exponents-roots

Exponent and Root of Complex Numbers

Exponent of Complex Numbers

» Play with the forms of the complex number

    → component form $a + i b$ $a+ib$

    → polar form $r (\cos θ + i \sin θ)$ $r(cos theta + i sin theta)$

    → exponent form $r e^{i θ}$ $re^(i theta)$

» Convert to the standard form of complex numbers $a + i b$ $a+ib$

    → eg: ${(a + i b)}^{c + i d}$ $(a+ib)^(c+id)$ : convert $(a + i b)$ $(a+ib)$ to polar form $r e^{i θ}$ $re^(i theta)$

    → eg: $r^{i d}$ $r^(id)$ : convert $r$ $r$ to $e^{\ln r}$ $e^(ln r)$

Power of i

» To calculate $i^{n}$ $i^n$

Remember $i^{4} = 1$ $i^4 = 1$ and $i^{2} = - 1$ $i^2=-1$ . Quickly derive the following using this. No need to memorize

    → express $n$ $n$ in the form $n = 4 p + 2 q + r$ $n=4p+2q+r$ , where $p, q, r \in ℕ$ $p,q, r in NN$ natural numbers.

    → $i^{n} = {(- 1)}^{q} \times i^{r}$ $i^n = (-1)^q xx i^r$

maths > complex-number > complex-arithmetic-properties-addition

Properties of Complex Addition

Properties of complex number arithmetic is almost same as real number arithmetic as Complex number arithmetic is nothing but extension of real number arithmetic.

Understanding Properties of Complex Arithmetic
» The properties of real number arithmetic is extended to include $i = \sqrt{- 1}$ $i=sqrt(-1)$ as a number that cannot be added or multiplied to other real-numbers.Properties of Complex numbers extend on properties of Real numbers.

» Complex Addition is closed.
    → $z_{1} + z_{2} \in ℂ$ $z_1 + z_2 in CC$

» Complex Addition is commutative.
    → $z_{1} + z_{2} = z_{2} + z_{1}$ $z_1 + z_2 = z_2 + z_1$

» Complex Addition is associative.
    → $z_{1} + (z_{2} + z_{3}) = (z_{1} + z_{2}) + z_{3}$ $z_1 + (z_2 +z_3) = (z_1+z_2)+z_3$

» Complex Additive identity is $0$ $0$ .
    → $z_{1} + 0 = z_{1}$ $z_1 + 0 = z_1$

» Complex Additive inverse of $z$ $z$ is $- z$ $-z$
    → $z_{1} + (- z_{1}) = 0$ $z_1 + (-z_1) = 0$

» Complex modulus of sum is less than or equal to sum of moduluses
    → $| z_{1} + z_{2} | \leq | z_{1} | + | z_{2} |$ $|z_1 + z_2| <= |z_1| + |z_2|$

maths > complex-number > complex-arithmetic-properties-multiplication

Properties of Complex Multiplication

» Complex Multiplication is closed.
    → $z_{1} \times z_{2} \in ℂ$ $z_1 xx z_2 in CC$

» Complex Multiplication is commutative.
    → $z_{1} \times z_{2} = z_{2} \times z_{1}$ $z_1 xx z_2 = z_2 xx z_1$

» Complex Multiplication is associative.
    → $z_{1} \times (z_{2} \times z_{3}) = (z_{1} \times z_{2}) \times z_{3}$ $z_1 xx (z_2 xx z_3) = (z_1 xx z_2) xx z_3$

» Complex Multiplicative identity is $1$ $1$ .
    → $z_{1} \times 1 = z_{1}$ $z_1 xx 1 = z_1$

» Complex Multiplicative inverse of $z$ $z$ is $\frac{1}{z}$ $1/z$ .
    → $z \times \frac{1}{z} = 1$ $z xx 1/(z) = 1$

» Complex Multiplication is distributive over complex addition.
    → $z_{1} \times (z_{2} + z_{3}) = z_{1} \times z_{2} + z_{1} \times z_{3}$ $z_1 xx (z_2 + z_3) = z_1 xx z_2 + z_1 xx z_3$

» Modulus of product is product of modulus.
    → $| z_{1} \times z_{2} | = | z_{1} | \times | z_{2} |$ $|z_1 xx z_2| = |z_1| xx |z_2|$

» argument of product is sum of arguments of multiplicand and multiplier.
    → $a r g (z_{1} \times z_{2}) = a r g (z_{1}) + a r g (z_{2})$ $arg (z_1 xx z_2) = arg(z_1) + arg(z_2)$

maths > complex-number > complex-arithmetic-properties-conjugate

Properties of complex conjugate

Properties of complex conjugate is discussed in detail.

» Complex conjugate

    → distributes into addition, multiplication, and power
    → $\bar{z_{1} + z_{2}}$ $bar(z_1+z_2)$ $= \bar{z_{1}} + \bar{z_{2}}$ $= bar(z_1) + bar(z_2)$
    → $\bar{z_{1} \times z_{2}}$ $bar(z_1xxz_2)$ $= \bar{z_{1}} \times \bar{z_{2}}$ $= bar(z_1) xx bar(z_2)$
    → $\bar{z^{n}}$ $bar(z^n)$ $= {(\bar{z})}^{n}$ $= (bar(z))^n$

    → modulus of the conjugate equals the modulus of the number
    → $| \bar{z} |$ $| bar(z)|$ $= | z |$ $= |z|$

    → argument of the conjugate is negative of the argument of the number
    → $a r g (\bar{z})$ $arg (bar(z))$ $= - a r g (z)$ $= - arg(z)$

maths > complex-number > complex-number-algebraic-identities

Algebraic Identities for Complex numbers

The algebraic identities of complex number is same as that for real numbers.

Complex Algebraic Identities

» All identities of real-numbers holds

→ ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ $(a+b)^2 = a^2+2ab+b^2$

→ ${(a - b)}^{2}$ $(a-b)^2$ , etc.