Complex Numbers : Argand Plane and Polar Form

maths > complex-number

Argand Plane and Polar Form

what you'll learn...

Overview

Complex Plane

» Real line extended to complex plane
    → Argand Plane 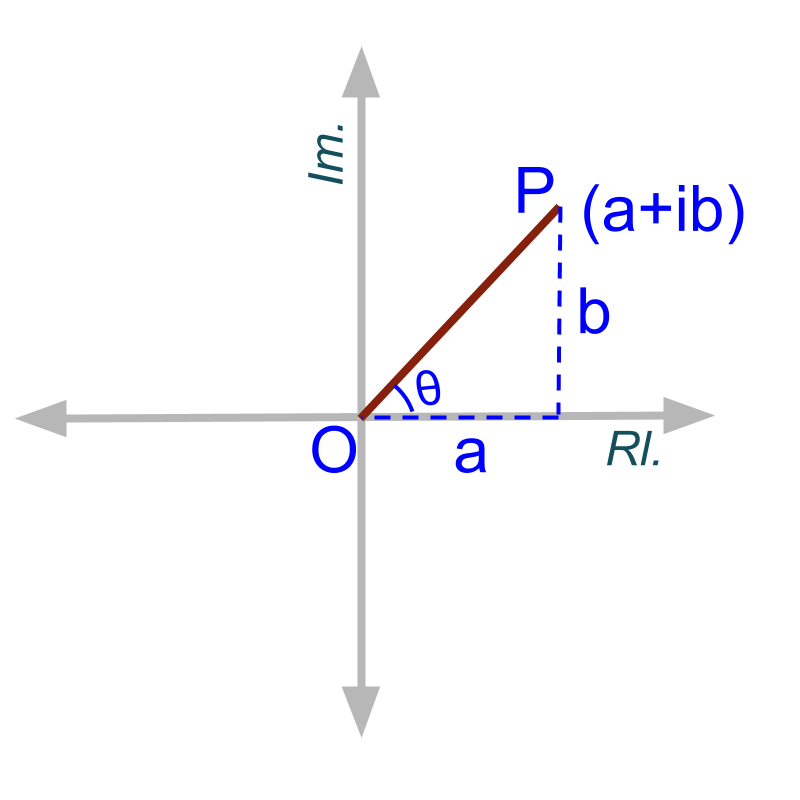» Complex plane for $a + i b$ $a+ib$

    → real part $a$ $a$ on real-axis or real-line

    → imaginary part $b$ $b$ on imaginary-axis

    → coordinate equivalent $(a, b)$ $(a,b)$

Modulus

» distance from origin $(0, 0)$ $(0,0)$ is modulus $r$ $r$ » $| a + i b |$ $|a+ib|$ $= r = \sqrt{a^{2} + b^{2}}$ $= r = sqrt(a^2+b^2)$
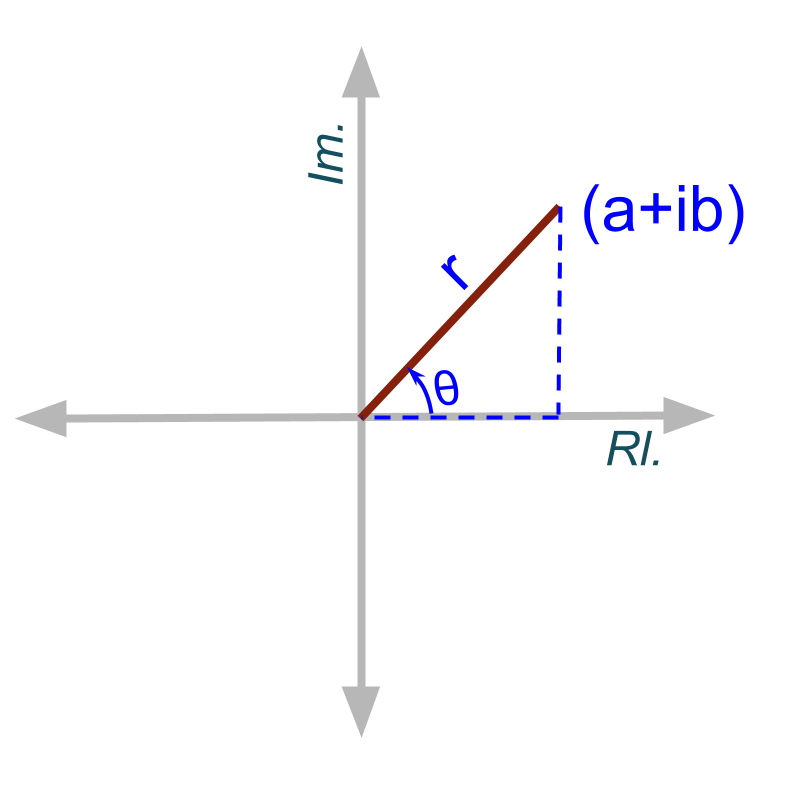by Pythagorean Theorem

Argument

» Angle with positive real-axis » $θ = \tan^{- 1} (\frac{b}{a})$ $theta = tan^(-1) (b/a)$

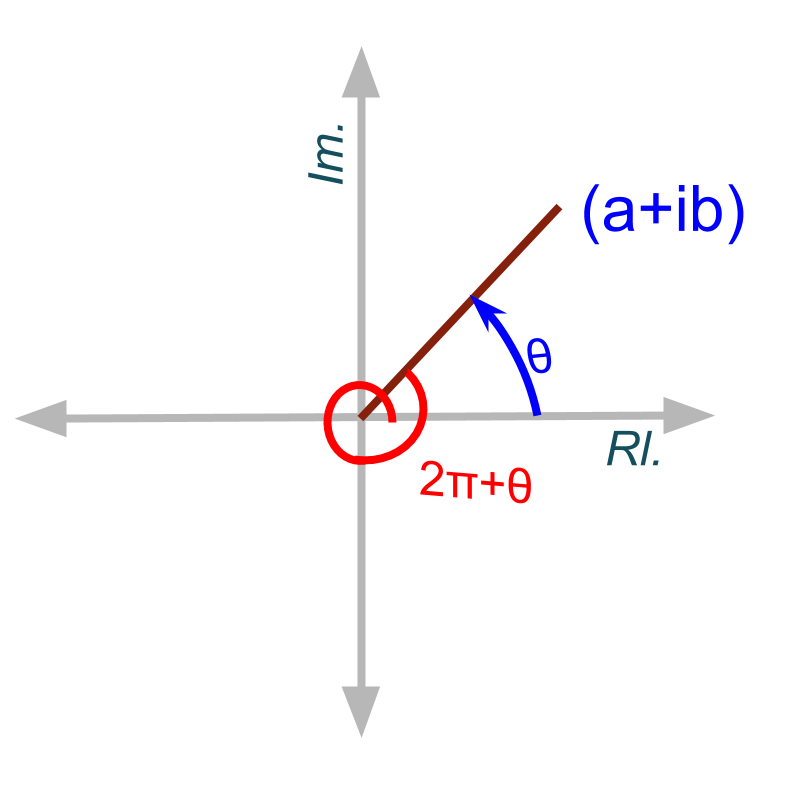» Arguments $= 2 n π + θ$ $= 2npi+theta$ where $n = 0, 1, 2, ...$ $n=0,1,2,...$

» Principal argument $= θ$ $= theta$ where $0 \leq θ < 2 π$ $0 <= theta < 2pi$

Polar form

$a + i b$ $a+ib$ $= r (\cos θ + i \sin θ)$ $=r(cos theta+i sin theta)$ $= r e^{i θ}$ $=re^(itheta)$

2 dimensional plane

Consider the plane with $x$ $x$ -axis and $y$ $y$ -axis, where a ordered pair of $(a, b)$ $(a,b)$ is represented with a point on the plane. This plane called '2D Cartesian Plane'.

The complex number representation is simplified to the form $a + i b$ $a+i b$ . This can also be considered as a ordered pair with the numbers $a, b$ $a,b$ being real numbers.

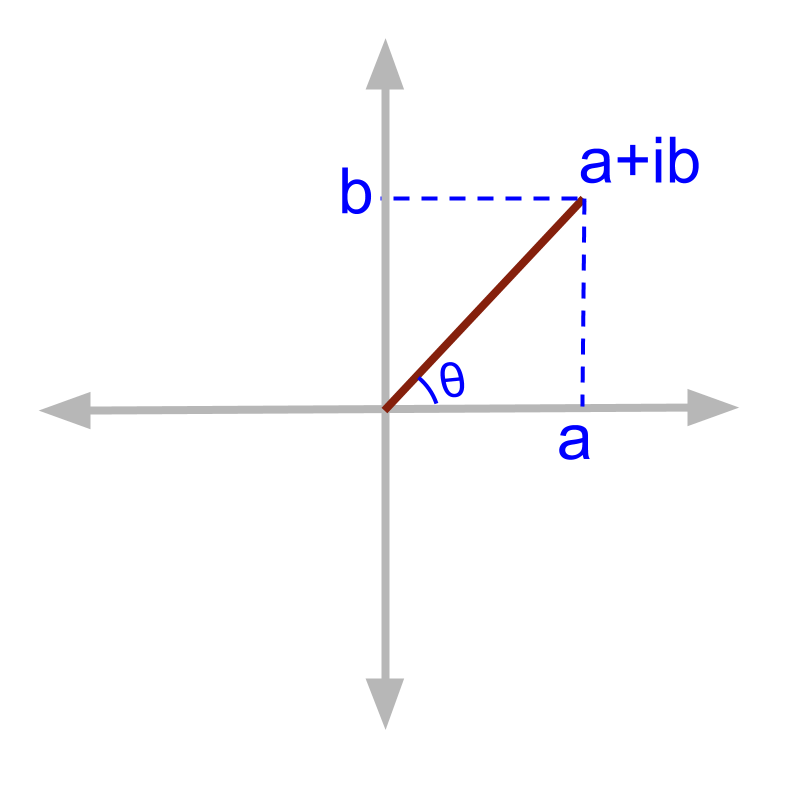
Similarity between points in 2D Cartesian plane and the complex numbers leads to definition of Complex plane. The complex plane is also called Argand plane named after the French Mathematician J R Argand.

Complex Plane or Argand Plane: A 2D plane in which a complex number $a + i b \in ℂ$ $a+i b in CC$ is assigned to a point $(a, b)$ $(a, b)$ as displacements along two axes of the plane.

A Complex number $a + i b$ $a+i b$ is represented on complex plane as shown in the figure. The axis on which real part $a$ $a$ is shown as displacement on that axis is called the real axis.

The axis on which imaginary part $b$ $b$ is shown as displacement on that axis is called the imaginary axis.

What is the point corresponding to the complex number $- 2 + i 6$ $-2+i6$ on the Argand plane?
The answer is ' $(- 2, 6)$ $(-2,6)$ '

summary

Real and Imaginary Axes: In the complex plane, the axis on which real part of complex numbers are mapped is called the real axis and the other axis on which the imaginary part of complex numbers are mapped is called the imaginary axis.

modulus of a complex number

A Complex number $a + i b$ $a+i b$ is represented on complex plane as shown in the figure. the length of the line segment between origin and the point represented by the complex number is ' $\sqrt{a^{2} + b^{2}}$ $sqrt(a^2+b^2)$ '

The length of the line segment $O P$ $OP$ is called modulus of the complex number. It is represented as $| z |$ $|z|$

$| z |$ $|z|$ is called modulus of z or mod z.

The word "modulus" means 'absolute measure without any additional information'.

In complex number, the absolute measure of the number without splitting into the real or imaginary parts is modulus.

Find the modulus of $1.1 - i$ $1.1-i$

The answer is ' $\sqrt{2.21}$ $sqrt(2.21)$ '

summary

Modulus: For a complex number $z = a + i b \in ℂ$ $z=a+i b in CC$ , the modulus of $z$ $z$ is given as $| z | = \sqrt{a^{2} + b^{2}}$ $|z| = sqrt(a^2+b^2)$

The length of line segment from origin to the point represented by complex number is the modulus of the complex number.

argument of a complex number

A Complex number $a + i b$ $a+i b$ is represented on complex plane as shown in the figure. The angle the line segment $O P$ $OP$ makes with the real axis is ' $\tan^{- 1} (\frac{b}{a})$ $tan^(-1)(b/a)$ '

The angle between the real axis in positive direction and the line segment $O P$ $OP$ is called the argument of the complex number.

In this case, the word "argument" means 'an independent element that plays a role in determining the value of something'.
For example the arguments of a function $f () = 2 x y + 3$ $f() = 2xy+3$ are the variables $x$ $x$ and $y$ $y$ . In this case, the arguments define the value of the function.

In complex numbers, the modulus provides the absolute value. In addition to the modulus, to completely specify the complex number, the additional independent element required is the "argument".

For $z = a + i b \in ℂ$ $z=a+i b in CC$ , argument is given by $arg z = \tan^{- 1} (\frac{b}{a})$ $text(arg) z = tan^(-1)(b/a)$

Find the argument of $1 + i$ $1+i$
The answer is ' $\tan^{- 1} 1$ $tan^(-1)1$ '

Argument: For a complex number $z = a + i b \in ℂ$ $z=a+i b in CC$ , the argument of $z$ $z$ is given as $arg z = \tan^{- 1} (\frac{b}{a})$ $text(arg) z = tan^(-1)(b/a)$

The angle made by the line segment with the real axis is the argument of the complex number.

The possible values of $\tan^{- 1} 1$ $tan^(-1)1$ are ' $\frac{n π}{4}$ $(n pi)/4$ where $n = 1, 3, 5, \dots$ $n = 1,3,5,cdots$ '.

The possible values of $\tan^{- 1} 1$ $tan^(-1)1$ , if the opposite side and adjacent sides are given as $1$ $1$ is different : $\frac{n π}{4}$ $(n pi)/4$ where $n = 1, 5, 9, \dots$ $n = 1,5,9,cdots$

Note that: $\tan^{- 1} 1 = \frac{n π}{4}$ $tan^(-1)1 = (n pi)/4$ where $n = 1, 3, 5, \dots$ $n = 1,3,5,cdots$ but

$\tan^{- 1} \frac{opposite-side = 1}{adjacent-side = 1} = \frac{n π}{4}$ $tan^(-1) (text(opposite-side)=1)/(text(adjacent-side)=1) = (n pi)/4$ where $n = 1, 5, 9, \dots$ $n = 1,5,9,cdots$ and

$\tan^{- 1} \frac{opposite-side = - 1}{adjacent-side = - 1} = \frac{n π}{4}$ $tan^(-1) (text(opposite-side)=-1)/(text(adjacent-side)=-1) = (n pi)/4$ where $n = 3, 7, 11, \dots$ $n = 3,7,11,cdots$

The argument of a complex number can be given in the form $2 n π + θ$ $2n pi + theta$ where $n = 0, 1, 2 ...$ $n=0,1,2...$ .

The argument corresponding to $n = 0$ $n=0$ is called the principal argument. The range of principal argument is $- π \leq θ \leq π$ $-pi <= theta <= pi$ .

range of argument

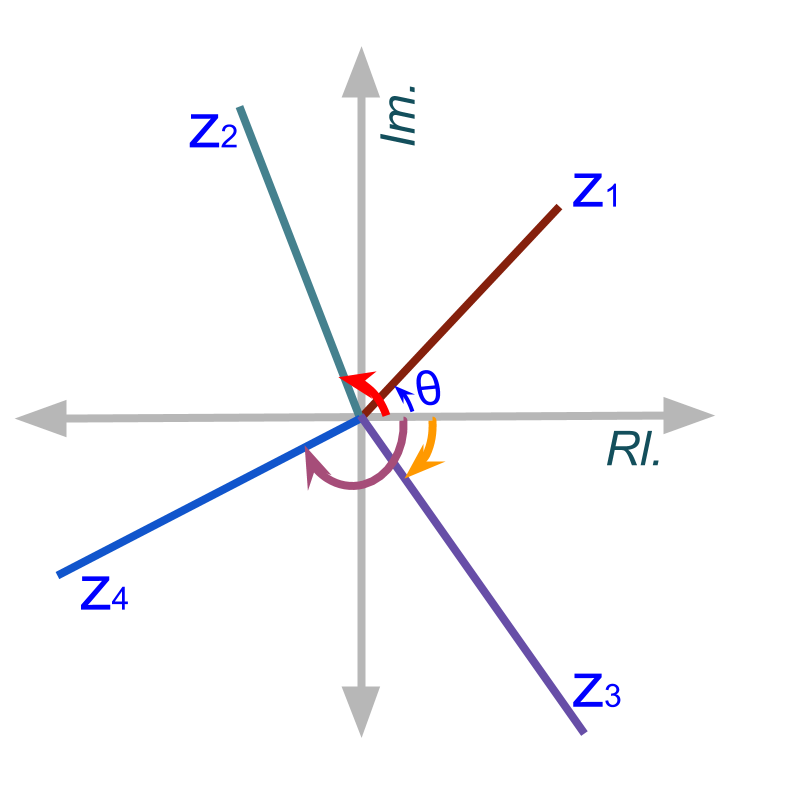
Given the complex numbers $z_{1}, z_{2}, z_{3}, z_{4}$ $z_1, z_2, z_3, z_4$ as shown in figure. The value of argument of complex numbers are
• $0 < arg z_{1} < \frac{π}{2}$ $0 < text(arg) z_1 < pi/2$
• $\frac{π}{2} < arg z_{2} < π$ $pi/2 < text(arg) z_2 < pi$
• $0 < arg z_{3} < - \frac{π}{2}$ $0< text(arg) z_3 <-pi/2$
• $- \frac{π}{2} < arg z_{4} < - π$ $-pi/2< text(arg) z_4 <-pi$

Find the principal argument of $1 - i$ $1-i$

The answer is ' $- \frac{π}{4}$ $-pi/4$ '

summary

Principal Argument: For a complex number $z = a + i b \in ℂ$ $z=a+i b in CC$ , the principal argument of $z$ $z$ is given as $arg z = \tan^{- 1} (\frac{b}{a})$ $text(arg) z = tan^(-1)(b/a)$ , where $- π \leq arg z \leq π$ $-pi <= text(arg) z <= pi$

Principal argument of a complex number is in the range $- π$ $-pi$ to $π$ $pi$ .

polar form

While introducing the generic form of complex numbers $a + i b$ $a+i b$ , it was discussed an equivalent form $r (\cos θ + i \sin θ)$ $r(cos theta + i sin theta)$ . A quick revision of the same with complex plane is given here.

A number $a + b i$ $a+b i$ is equivalently given as $r (\cos θ + i \sin θ)$ $r(cos theta + i sin theta)$ where $r = \sqrt{a^{2} + b^{2}}$ $r = sqrt(a^2+b^2)$ and $θ = \tan^{- 1} (\frac{b}{a})$ $theta = tan^(-1)(b/a)$ .

$r (\cos θ + i \sin θ)$ $r(cos theta + i sin theta)$ is called the polar form or polar representation of the complex number.

Convert $1 + i$ $1+i$ into polar form.

The answer is ' $\sqrt{2} (\cos (\frac{π}{4}) + i \sin (\frac{π}{4}))$ $sqrt(2)(cos(pi/4)+i sin(pi/4))$ '

summary

Polar Form: A number in the form $a + b i$ $a+bi$ is equivalently given as
$= r (\cos (θ + 2 n π)$ $quad quad = r (cos (theta+ 2n pi)$
$+ i \sin (θ + 2 n π))$ $quad quad quad quad + i sin (theta+ 2n pi))$
where $r = \sqrt{a^{2} + b^{2}}$ $r = sqrt(a^2+b^2)$ ,
$θ = \tan^{- 1} (\frac{b}{a})$ $theta = tan^(-1)(b/a)$ .

Polar form of a complex number is $r (\cos θ + i \sin θ)$ $r (cos theta + i sin theta)$

Outline

The outline of material to learn "complex numbers" is as follows.

Note : Click here for detailed overview of Complex-Numbers

→ Complex Numbers in Number System

→ Representation of Complex Number (incomplete)

→ Euler's Formula

→ Generic Form of Complex Numbers

→ Argand Plane & Polar form

→ Complex Number Arithmetic Applications

→ Understanding Complex Artithmetics

→ Addition & Subtraction

→ Multiplication, Conjugate, & Division

→ Exponents & Roots

→ Properties of Addition

→ Properties of Multiplication

→ Properties of Conjugate

→ Algebraic Identities