Complex Numbers : Complex Number Arithmetics & modeling sine waves

maths > complex-number

Complex Number Arithmetics & modeling sine waves

what you'll learn...

Overview

Basis of Complex Number Arithmetic

» Modeling sine waves
    → same frequency $ω$ $omega$

    → different amplitude $r$ $r$

    → different phase $ϕ$ $phi$ » amplitude and phase

    → $\sin 1.1 x$ $sin1.1x$ is shown in blue

    → $2.5 \sin (1.1 x + 0.7)$ $2.5sin(1.1x+0.7)$ is shown in orange
$2.5$ $2.5$ amplitude is the size change.
$0.7$ $0.7$ phase is the horizontal shift.

Modeling sine waves

» Algebraic explanation
    → $r \sin (ω x + ϕ)$ $r sin(omega x + phi)$

substitute $\sin (A + B)$ $sin(A+B)$ formula
    → $= r (\cos ϕ \sin ω x$ $= r(cos phi sin omega x$ $+ \sin ϕ \cos ω x)$ $+ sin phi cos omega x)$

substitute $\cos ω x = i \sin ω x$ $cos omega x = i sin omega x$
    → $= r (\cos ϕ + i \sin ϕ) \sin ω x$ $= r(cos phi + i sin phi)sin omega x$

substitute coordinate form of complex number
    → $= (a + i b) \sin ω x$ $=(a+ib)sin omega x$

considering that $ω$ $omega$ is a constant, $\sin ω x$ $sin omega x$ can be taken off the expression.
    → $= a + i b$ $=a+ib$

» Geometrical explanation
    → $r \sin (ω x + ϕ)$ $r sin(omega x + phi)$
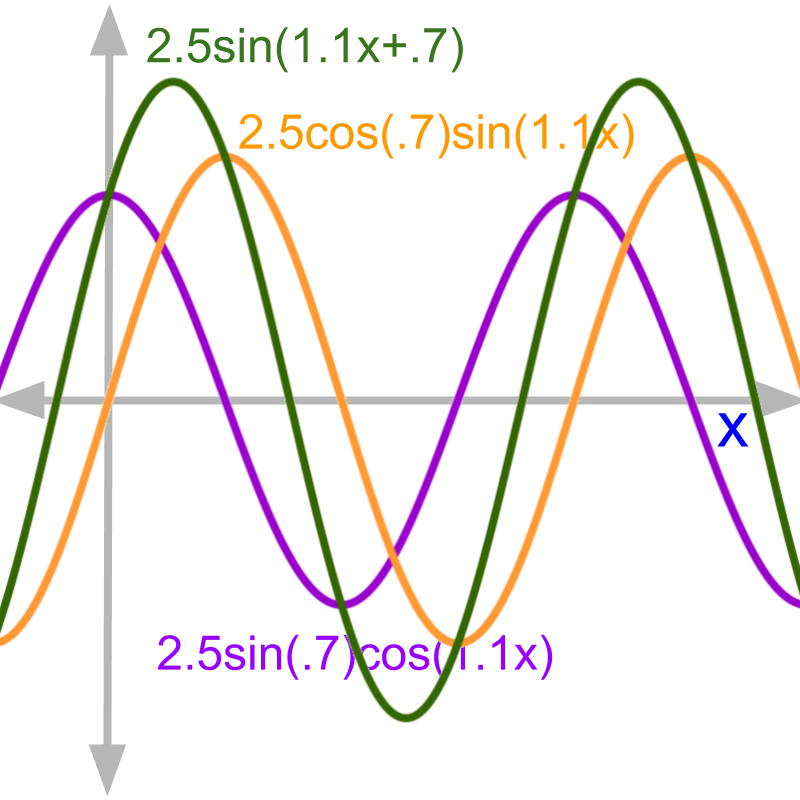
A sine wave with an amplitude and phase can be equivalently represented as sum of a sine wave and a cosine wave of different amplitudes and $0$ $0$ phase.       $2.5 \sin (1.1 x + .7)$ $2.5 sin(1.1x+.7)$
      $= 2.5 \cos (.7) \sin (1.1 x)$ $= 2.5 cos(.7)sin(1.1x)$
      $+ 2.5 \sin (0.7) \cos (1.1 x)$ $+ 2.5 sin(0.7)cos(1.1x)$

» Sine waves of same frequency is modeled with complex number $a + i b$ $a+ib$
    → Complex addition as per sine wave addition
    → Complex multiplication as per sine wave interaction

complex arithmetics

In case of real numbers, Arithmetic operations makes sense as quantities are measured in real numbers.
• add and subtract : $3.3$ $3.3$ m/sec + $2.1$ $2.1$ m/sec speed
• multiply and divide : $4.2$ $4.2$ meter $\times 1.1$ $xx 1.1$ coins per meter

It is so far explained that complex numbers are solutions to polynomials. In that context, what does it mean to
• add and subtract complex numbers
• multiply and divide complex numbers

This topic explains that from application perspective.

Most authors directly discuss the abstraction without any need to understand an application perspective. And, when one comes across the application where the concepts are relevant, at that time he/she has to put in extra effort to understand the abstraction in the application context.

As part of this course one application context is explained.

Complex numbers serve as mathematical model for
• Alternating Current(AC) sine waves with amplitude and phase, and the passive elements in the AC circuits that modify amplitude and phase of the input.
• Analysis of Systems that modify amplitude and phase of input.
• Analysis of Signals that can be expressed as sum of sine waves of different frequencies, amplitude and phase.
• Abstracted 2D plane : called complex plane, and abstract problems in that.

Note again :
• AC with amplitude and phase
• Systems that change amplitude and phase of input.

The key points in the above are 'Amplitude and phase'. The frequency of sine waves is a constant in these.

Complex numbers model amplitude and phase for
• sine waves ( amplitude and phase)
• passive elements (modification of amplitude and phase)

A sine wave of frequency $f$ $f$ with amplitude $r$ $r$ and phase $θ$ $theta$ is equivalently a complex number $r \cos θ + i r \sin θ$ $r cos theta + i r sin theta$ .

An element acts on an incoming sine wave and affects the amplitude and phase. The factor by which it modifies $r$ $r$ and the amount by which it shifts the phase $θ$ $theta$ is equivalently a complex number $r \cos θ + i \sin θ$ $r cos theta + i sin theta$ .

Note 1: These statements are explained in topic 'Physics : Alternating Current'

Note 2: For the super-scientific readers -- The passive elements does rate of change and continuous aggregate of input sine wave. In the case of sine waves, those are modeled as differentiation and integration, and effectively result in a phase shift.

The later part of this page "Complex Number : Modeling sine waves" provides proofs and detailed explanation on how complex number is used in sine wave with amplitude and phase.

When the frequency of sine wave is constant :
• Addition of two sine waves with different amplitude and phase results in one sine wave of result-amplitude and result-phase. This is modeled by complex number addition / subtraction.
• Interaction of one sine wave input by a passive component that changes amplitude and phase, results in one sine wave of result-amplitude and result-phase. This is modeled by complex number multiplication and division.

Complex numbers provide the mathematical model for amplitude and phase of sine waves and how they are modified.

Complex numbers are a tool to approach problems in 2D complex plane.

Complex Arithmetic is understood from these applications perspective.

summary

Application Scenario: Complex number $a + i b$ $a+ib$ model
• a sine wave of amplitude and phase
• an element that modifies amplitude and phase of sine waves
Mathematical operations (like addition, subtraction, multiplication, division) between complex numbers are defined for that model.

modelling sine waves

It is quite easy to introduce the following in abstract definitions:
• complex numbers,
• the arithmetic operations (addition, multiplication, powers, etc.) and
• properties (commutative, distributive, etc.)

Apart from understanding the abstract concepts, it will immensely benefit to understand application scenarios. This topic explains this.

One has to apply his or her mind to understand. Hope you enjoy exercising your brains.

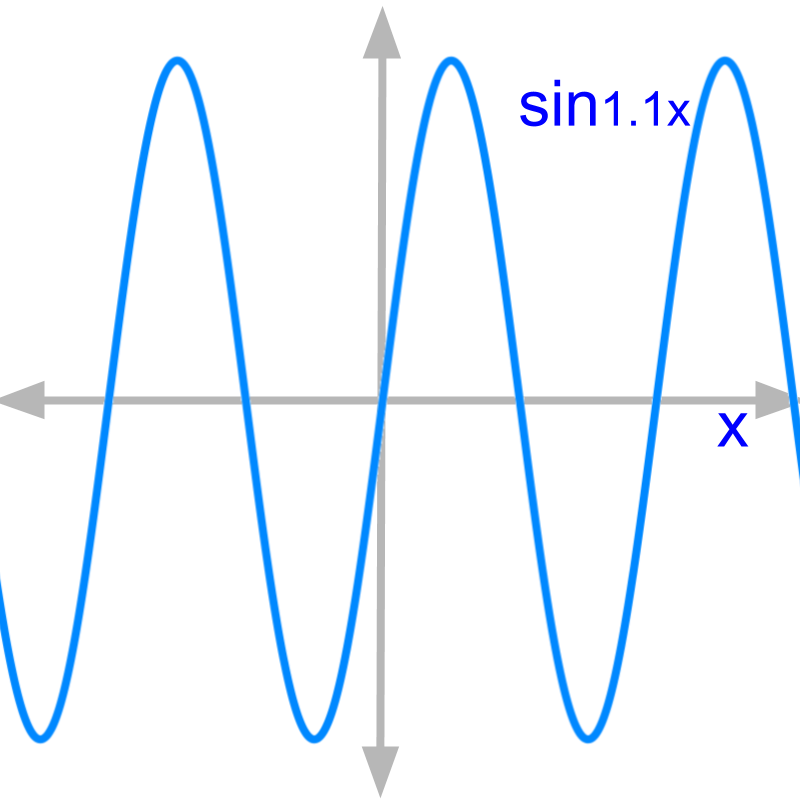
The figure shows a sine wave. It is the plot for $f (x) = \sin (1.1 x)$ $f(x)=sin(1.1x)$

sine wave with amplitude and phase illustration

The figure shows the sine wave $\sin (1.1 x)$ $sin(1.1x)$ in blue. In comparison, the sine wave in orange has different magnitude and phase. Phase is the horizontal shift the wave is having as shown in the figure.

The curve in orange is for $f (x) = 2.5 \sin (1.1 x + .7)$ $f(x)=2.5sin(1.1x+.7)$ .

This plot has $r = 2.5$ $r=2.5$ and $θ = 0.7 radian$ $theta = 0.7 text(radian)$ .
Complex number $2.5 (\cos (0.7) + i \sin (0.7))$ $2.5(cos(0.7)+ i sin(0.7))$ represents the wave. We will explain this in next few pages.

A sine wave with an amplitude and phase can be equivalently represented as sum of a sine wave and a cosine wave of different amplitudes and $0$ $0$ phase.

This is shown with a plot of sine and sum of (sin and cos) in the figure (explained in the next page).

Mathematical Proof:
$r \sin (ω x + ϕ)$ $r sin (omega x + phi)$ Substituting sin(a+b) formula
$= a \sin (ω x) + b \cos (ω x)$ $quad quad = a sin(omega x) + b cos(omega x)$
Where $a = r \cos ϕ$ $a = r cos phi$ and $b = r \sin ϕ$ $b= r sin phi$
Substituting $\cos (ω x) = i \sin (ω x)$ $cos(omega x ) = i sin(omega x)$
$r \sin (ω x + ϕ)$ $r sin (omega x + phi)$
$= a \sin (ω x) + i b \sin (ω x)$ $quad quad = a sin(omega x) + ib sin(omega x)$
$= (a + i b) \sin (ω x)$ $quad quad = (a+ib) sin(omega x)$

Inverse of that, sum of sine and cosine waves of different amplitudes make a sine wave of a certain phase.

Prove
$a \sin (ω x) + b \cos (ω x)$ $a sin(omega x) + b cos(omega x)$
$= r \sin (ω x + ϕ)$ $= r sin (omega x + phi)$

sine wave with phase as a sum of sine and cosine without phase

The figure shows three plots. The sine wave in green equals the sum of sine waves in orange and purple. The sine wave in green is $2.5 \sin (1.1 x + .7)$ $2.5sin(1.1x+.7)$

The sine wave in orange is $2.5 \cos (.7) \sin (1.1 x)$ $2.5cos(.7)sin(1.1x)$

The sine wave in purple is $2.5 \sin (.7) \cos (1.1 x)$ $2.5sin(.7)cos(1.1x)$

It can be verified that the first equals the sum of latter two at every point.

It is easy to prove that the addition of two sine waves of different phase results in another sine wave.

Prove
$r_{1} \sin (ω x + ϕ_{1}) + r_{2} \sin (ω x + ϕ_{2})$ $r_1 sin (omega x + phi_1) + r_2 sin (omega x + phi_2)$
$= a_{3} \sin (ω x) + b_{3} \cos (ω x)$ $= a_3 sin(omega x) + b_3 cos(omega x)$

prove that
$a_{3} = a_{1} + a_{2}$ $a_3 = a_1 + a_2$
$b_{3} = b_{1} + b_{2}$ $b_3 = b_1 + b_2$

This uses only trigonometry to prove the results. The complex number models this addition.

The sine waves, when passing through passive elements (resistors, capacitors, inductors) in AC circuits, undergo change in amplitude and phase. The passive elements are modeled as complex numbers.

The change in amplitude is given by $r$ $r$ and the change in phase is given by $θ$ $theta$ , then the passive element is given as a complex number $r (\cos θ + i \sin θ)$ $r(cos theta + i sin theta)$ .

It is easy to prove that the interaction of sine wave with an element that modifies amplitude and phase, is complex multiplication.
$r_{1} \sin (ω x + ϕ_{1})$ $r_1 sin (omega x + phi_1)$ is the sine wave
$(r_{2}, ϕ_{2})$ $(r_2, phi_2)$ is the element given as an ordered pair.

Multiplication is given by
Prove
$r_{1} \sin (ω x + ϕ_{1}) \times (r_{2}, ϕ_{2})$ $r_1 sin (omega x + phi_1) xx (r_2, phi_2)$
$= r_{1} r_{2} \sin (ω x + ϕ_{1} + ϕ_{2})$ $= r_1r_2 sin (omega x + phi_1+ phi_2)$
$= a_{3} \sin (ω x) + b_{3} \cos (ω x)$ $= a_3 sin(omega x) + b_3 cos(omega x)$

prove that
$a_{3} = a_{1} a_{2} - b_{1} b_{2}$ $a_3 = a_1a_2 - b_1b_2$
$b_{3} = a_{1} b_{1} + a_{2} b_{2}$ $b_3 = a_1b_1 + a_2b_2$

This uses only trigonometry to prove the results. The complex number models this.

Electrical current, Sine waves (having constant frequency) of different amplitude and phase is mathematically modeled with complex numbers.

Electrical passive elements that affect the amplitude and phase of sine waves is mathematically modeled with complex numbers.

Complex arithmetics (addition, multiplication, etc.) models the interaction between the sine waves and the elements.

Complex number is used to model Sine waves of same frequency, varying in amplitude and phase.

Complex number is used to model Systems that modify amplitudes and phase.

summary

Application Details:
• Sine wave is modeled as $(a + b i) \sin (ω x)$ $(a + bi)sin(omega x)$
• sine wave addition $[(a_{1} + a_{2}) + i (b_{1} + b_{2})] \sin (ω x)$ $[(a_1+a_2)+ i(b_1 + b_2)]sin(omega x)$
• sine wave interaction with an element as multiplication $[(a_{1} a_{2} - b_{1} b_{2}) + i (a_{1} b_{1} + a_{2} b_{2})] \sin (ω x)$ $[(a_1a_2 - b_1b_2) + i(a_1b_1 + a_2b_2)] sin(omega x)$

Complex number arithmetic is defined for these applications
• Complex number $a + i b$ $a + ib$
• Complex number addition $(a_{1} + a_{2}) + i (b_{1} + b_{2})$ $(a_1+a_2) + i(b_1 + b_2)$
• Complex number multiplication
$(a_{1} a_{2} - b_{1} b_{2})$ $(a_1a_2 - b_1b_2)$
$+ i (a_{1} b_{1} + a_{2} b_{2})$ $quad quad + i(a_1b_1 + a_2b_2)$

Outline

The outline of material to learn "complex numbers" is as follows.

Note : Click here for detailed overview of Complex-Numbers

→ Complex Numbers in Number System

→ Representation of Complex Number (incomplete)

→ Euler's Formula

→ Generic Form of Complex Numbers

→ Argand Plane & Polar form

→ Complex Number Arithmetic Applications

→ Understanding Complex Artithmetics

→ Addition & Subtraction

→ Multiplication, Conjugate, & Division

→ Exponents & Roots

→ Properties of Addition

→ Properties of Multiplication

→ Properties of Conjugate

→ Algebraic Identities