
what you'll learn...
overview
Triangles are defined by independent parameters. Usually, the three independent parameters are chosen from primary parameters -- the three sides and the three angles.
The sum of two sides, or perimeter of the triangle, etc. are secondary parameters.
If one or more of given parameters is of secondary type, then how to construct the specified triangle? A short overview of approaching such problems is provided in this lesson.
An overview of constructing triangles with angle-side-sum of two sides is provided. Sum of two sides is a secondary parameter.
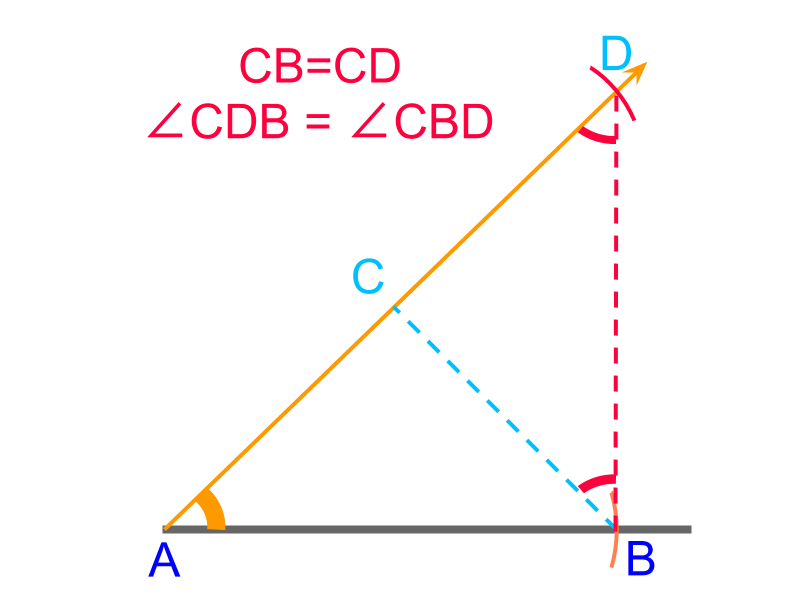
An overview of constructing triangles with angle-side-difference between two sides is provided. Difference between two sides is a secondary parameter.
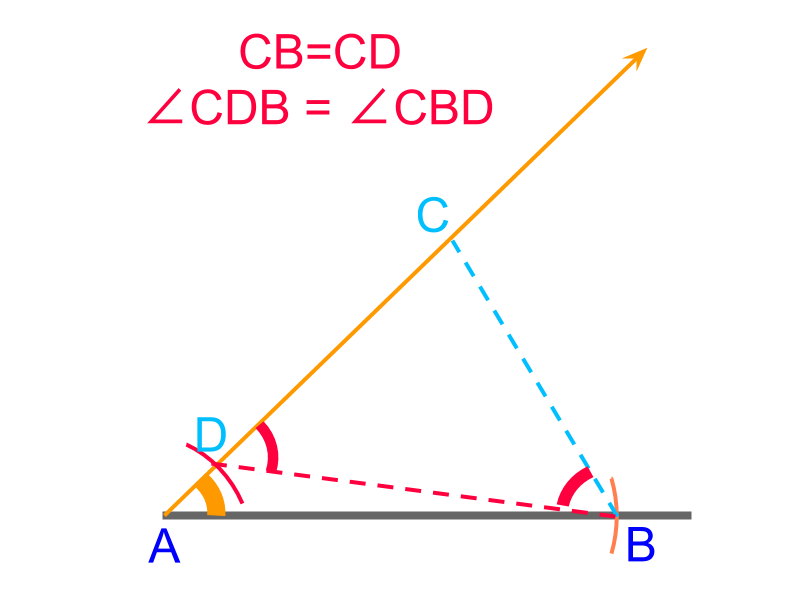
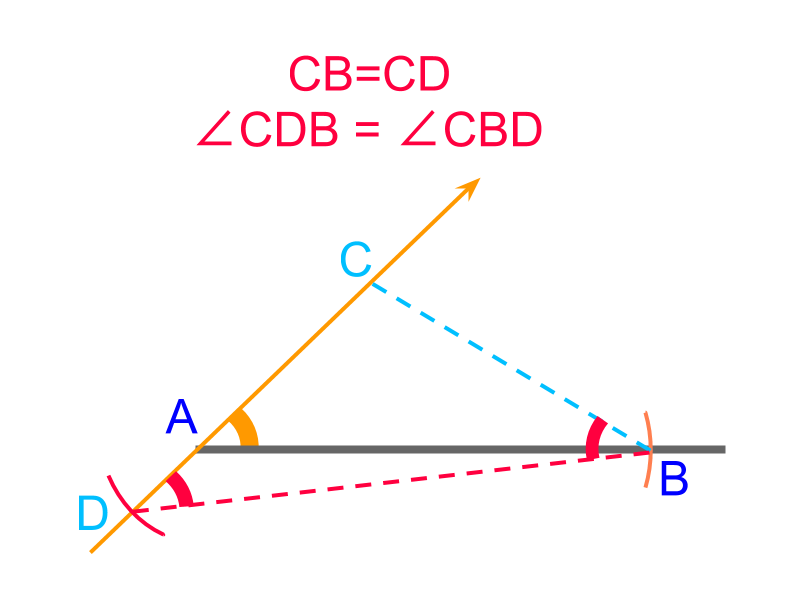
An overview of constructing triangles with angle-side-negative difference between two sides is provided. Negative difference between two sides is a secondary parameter.
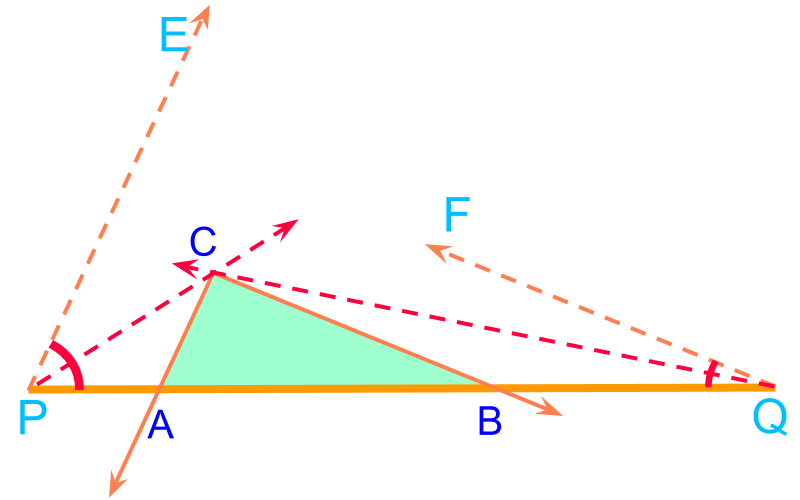
An overview of constructing triangles with angle-angle-perimeter is provided. Perimeter is a secondary parameter.
recap
To construct any shape, the fundamental elements we use are
• Construct a line passing through the two given points using a ruler or scale (collinear points)
• Construct a ray at the given angle using a protractor (equiangular points)
• Construct an arc at the given distance using a compass and a ruler or scale (equidistant points)
• construct a parallel line using a set-square and a scale or another set-square. (points on a parallel)
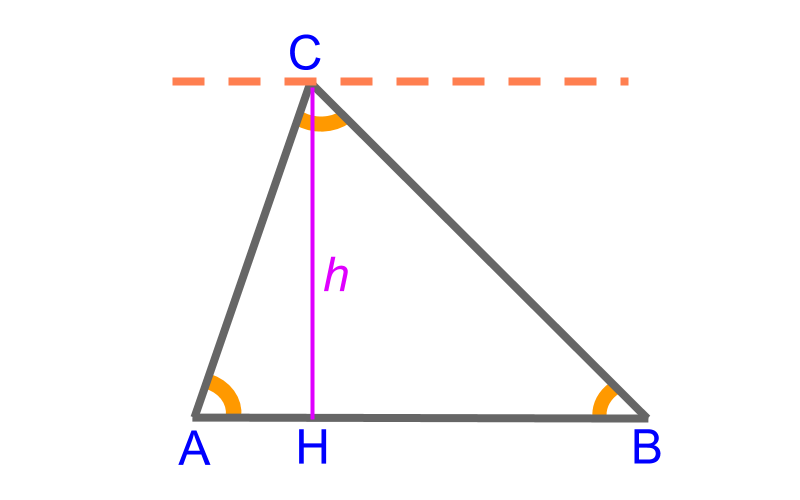 Triangle has the following measurements as the parameters
Triangle has the following measurements as the parameters
• side
• side
• side
• angle
• angle
• angle
• altitude or height of triangle
These are parameters in total. Among these , any independent parameters define a triangle. Other parameters can be derived from the given three parameters.
Note that the three angles are not truly independent as These parameters are basic parameters.
Earlier we studied about construction of triangles. To construct a triangle, one of the following set of parameters is provided.
• side-side-side (sss)
• side-angle-side (sas)
• angle-side-angle (asa)
In these, each of the parameters directly provides one of sides or angles
derived parameters
Apart from the basic parameters, a derived parameter can be provided.
Examples of "derived" parameters are
sum of two sides
difference between two sides
perimeter of the triangle
If the following are provided, how to construct the triangle?
side-angle-sum of two sides
side-angle-difference between two sides
perimeter-angle-angle
With trigonometry or with coordinate geometry, the given parameters can be converted to basic parameters. But, the objective of geometrical construction is to figure out the shape (the triangle) without any calculations.
In this lesson, construction of triangles with derived or secondary parameters is explained.
side-angle-sum of two sides
To construct a triangle, "side-angle-sum of other two sides" is provided. The given angle with two line segments of given side and sum of sides are directly constructed using the given parameters.
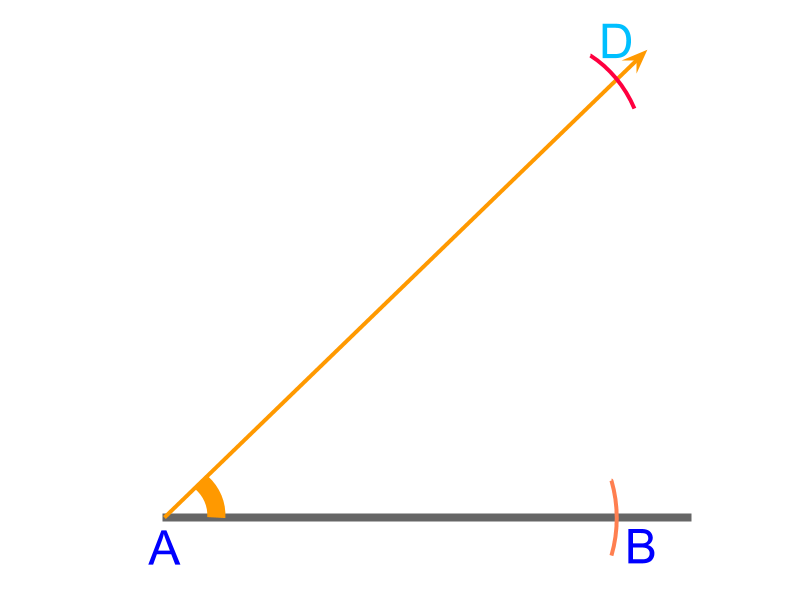
To construct a triangle with given "side-angle-sum of other two sides" cm, , and cm.
• Construct a line and mark side with a compass measuring cm
• measure angle and draw a ray from point
• measure cm in a compass and draw an arc cutting the ray at
This is directly constructed from the given parameters.
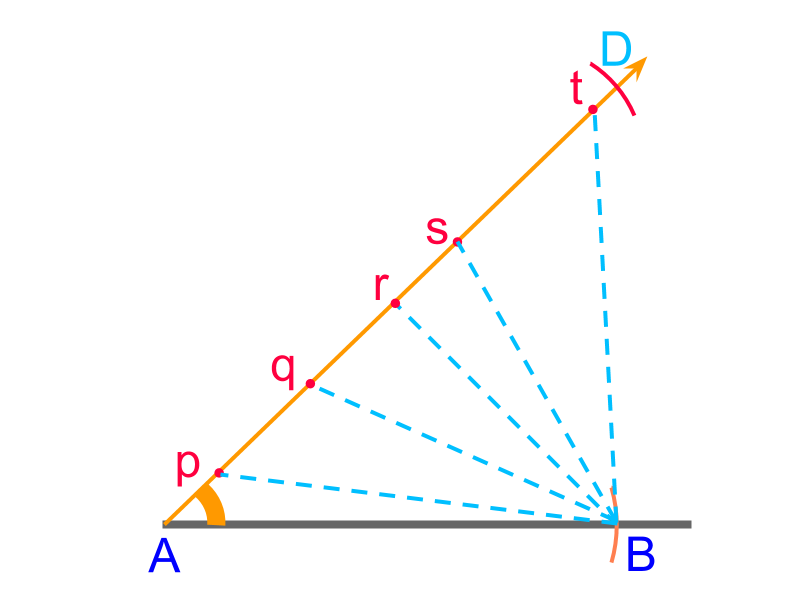
With given "side-angle-sum of two sides" we constructed , and at the given angle . The objective now is to locate the point in the line .
Consider points , , , , and on line . The following are observed.
•
•
• It is noted that at a single position between the points and , the point is located such that .
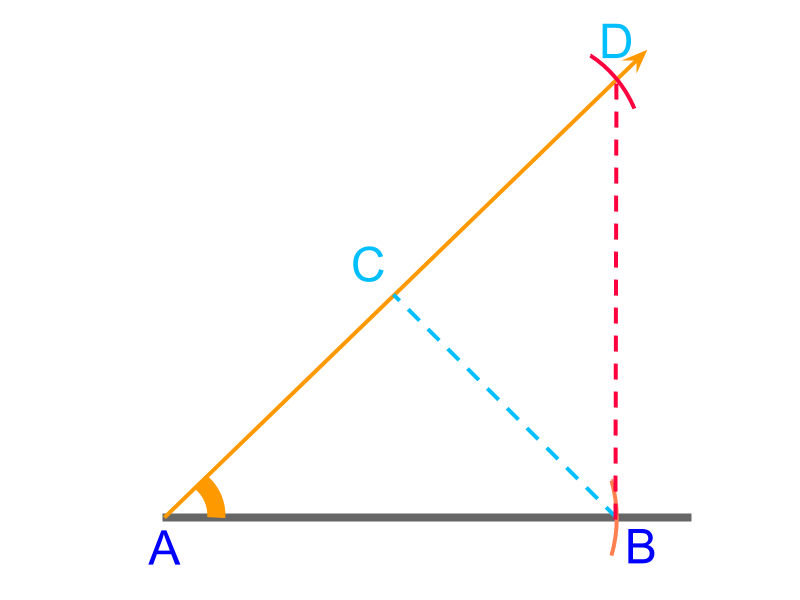
The point is visualized in such that . The line segments and are equal, as the triangle is isosceles

It is observed that is isosceles and only angle and base are available. The position of point is not yet marked. It is shown in the figure to visualize. To help in identifying the point , one the following properties is used :
• two angles of an isosceles triangles are equal.
• a perpendicular bisector on the base of isosceles triangle passes through the third vertex.
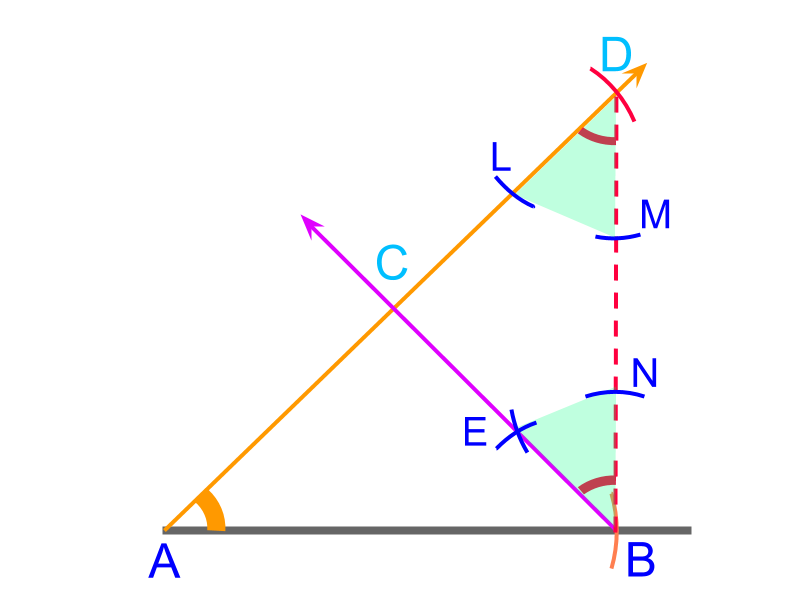
Using the property that
two angles of an isosceles triangles are equal.
The angle can be copied using a compass to mark line . The point of intersection of and is the point .
is constructed.
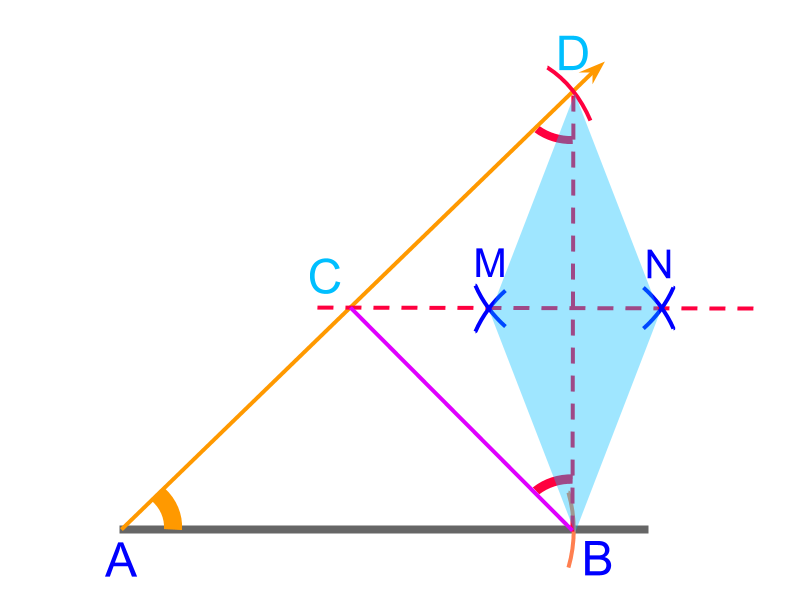
Using the property that
the perpendicular bisector on the base of isosceles triangle passes through the third vertex,
The line is drawn as bisector of . The point of intersection of and is the point .
is constructed.
summary

Construction of Side-Angle-Sum of 2 Sides triangle : Visualize the point and the is isosceles triangle.
Locate point by one of the following methods.
• copy the angle
• draw perpendicular bisector on the base.
side-angle-difference between other two sides
To construct a triangle, "side-angle-difference between other two sides" is provided. The given angle with two line segments of given side and difference between sides are directly constructed using the given parameters.
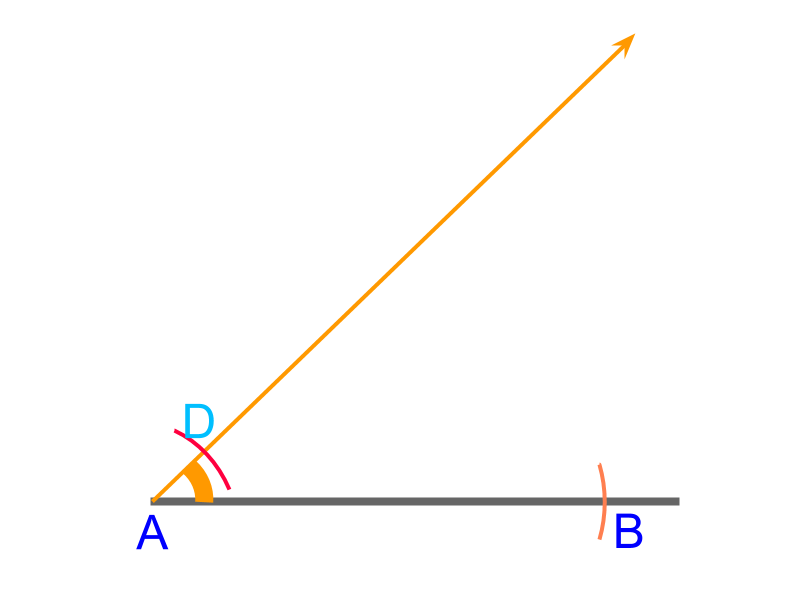
To construct a triangle with given "side-angle-difference between other two sides" cm, , and cm.
• Construct a line and mark side with a compass measuring cm
• measure angle and draw a ray from point
• measure cm in a compass and draw an arc cutting the ray at
This is directly constructed from the given parameters.

The objective now is to locate the point in the line .
Consider points , , , , and on line . The following properties are noted for points and in the line
•
•
• It is noted that at a single position in , the point is located such that .
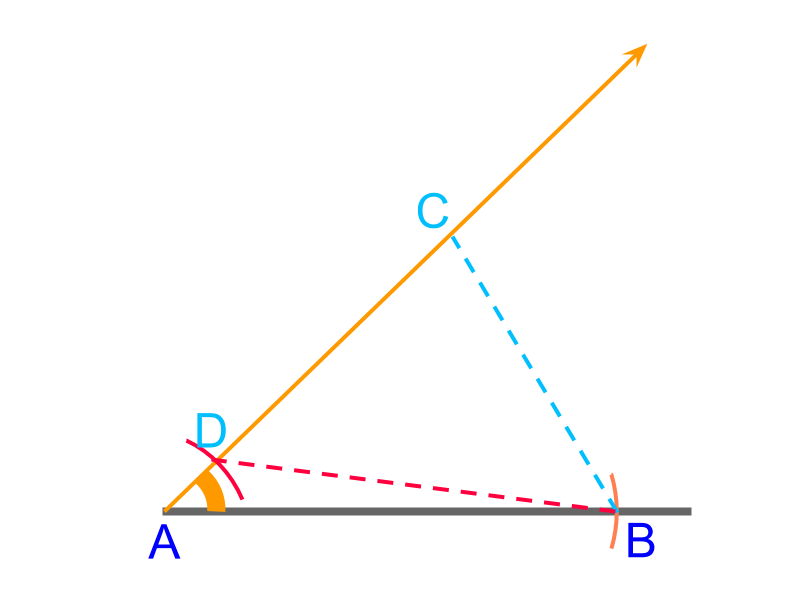
The point is visualized in such that . The following are useful observations that will help to locate the point along
• the line segments and are equal
• the triangle is isosceles

The position of point is not yet marked. It is shown in figure to visualize. The following properties are helpful in identifying the point .
• two angles of an isosceles triangles are equal.
• a perpendicular bisector on the base of isosceles triangle passes through the third vertex
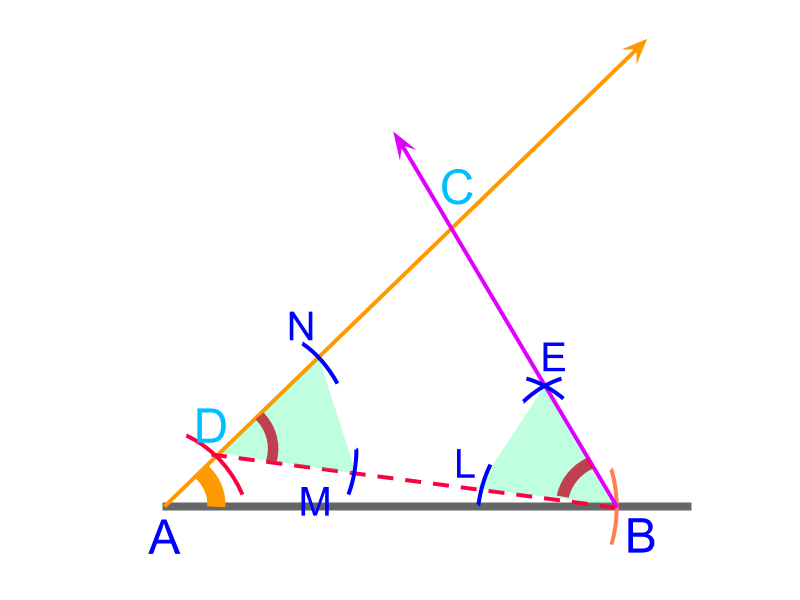
Using the property that
two angles of an isosceles triangles are equal.
The angle is copied using a compass to mark line
The point of intersection of rays and is the point .
is constructed.
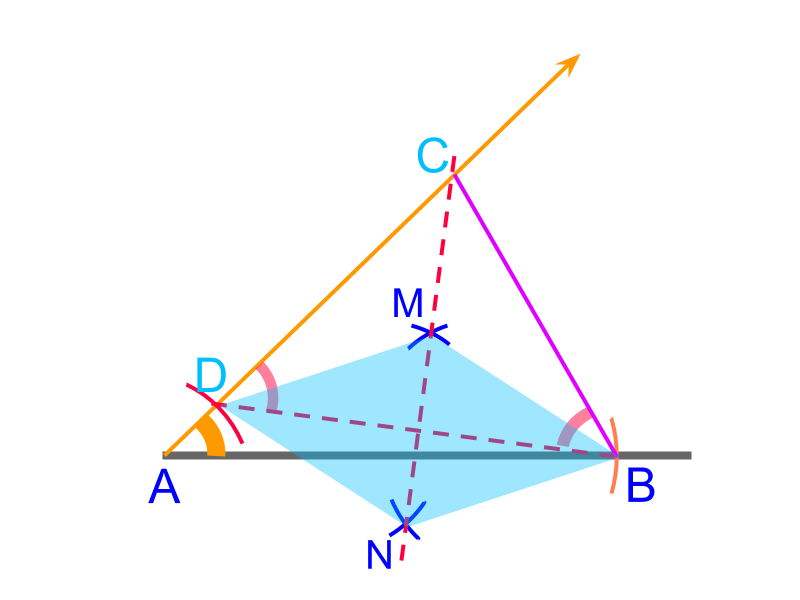
Using the property that
the perpendicular bisector on the base of isosceles triangle passes through the third vertex,
The line is constructed as the bisector of . The point of intersection of and is the point .
is constructed.
summary

Construction of Side-Angle-Difference between 2 Sides of triangle :Visualize that at point , the is isosceles triangle.
Locate point with one of the following methods.
• copy the angle
• draw perpendicular bisector on the base.
side-angle-difference between other two sides

To construct a triangle with given "side-angle-difference between other two sides" cm, , and cm OR cm.
• Construct a line and mark measuring cm
• measure angle and draw a ray from point
• measure cm and draw an arc cutting the ray at at the back-end of the ray, as shown in the figure.
This is directly constructed from the given parameters.
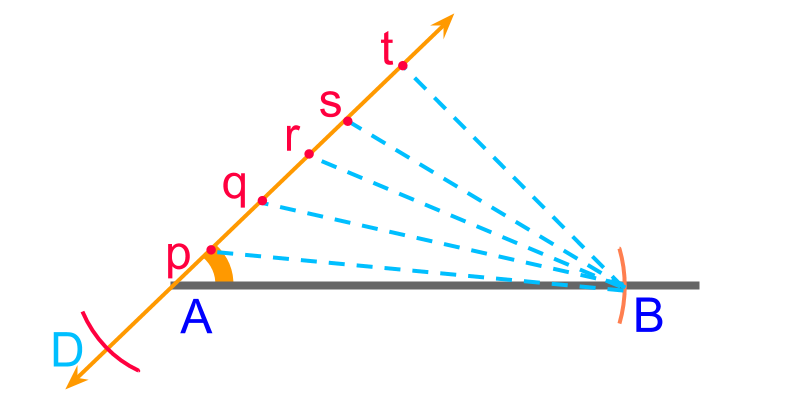
The objective now is to locate the point in the line .
Consider points , , , , and on line . The following property is noted for points and in the line
•
•
• It is noted that at a single position in , the point is located such that .
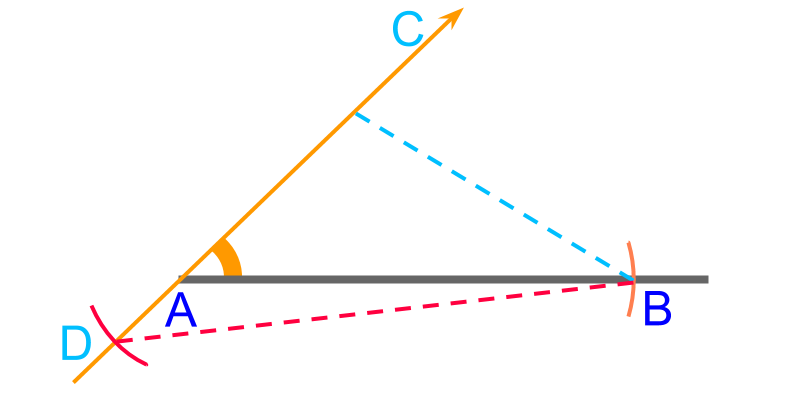
The point is visualized in such that . The following are useful observations that will help to locate the point along
• the line segments and are equal
• the triangle is isosceles

The position of point is not yet marked. It is shown in the figure to visualize. The following property helps in identifying the point .
• two angles of an isosceles triangles are equal.
• a perpendicular bisector on the base of isosceles triangle passes through the third vertex
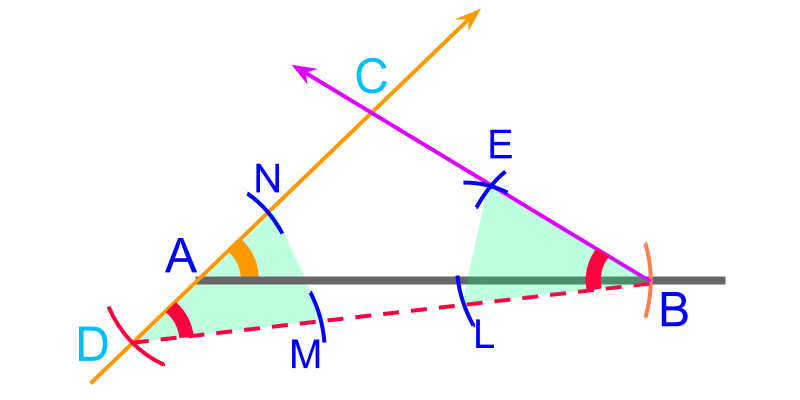
Using the property that
two angles of an isosceles triangles are equal.
The angle can be copied using a compass to mark line .
The point of intersection of rays and is the point .
is constructed.
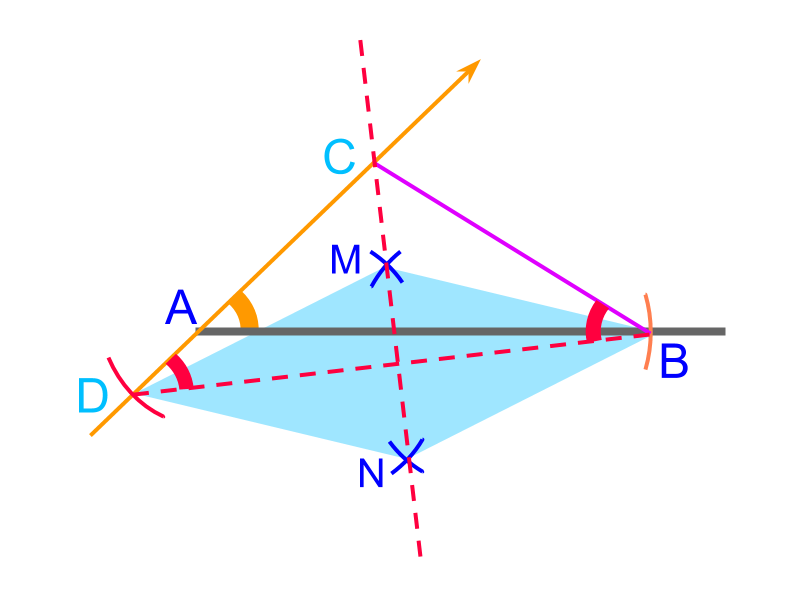
Using the property that
the perpendicular bisector on the base of isosceles triangle passes through the third vertex,
The line is constructed as the bisector of . The point of intersection of and is the point .
is constructed.
summary

Construction of Side-Angle-Negative difference between 2 Sides of triangle : Visualize that at point , the is isosceles triangle.
Locate point with one of the following methods.
• copy the angle
• draw perpendicular bisector on the base.
angle-angle-perimeter
To construct a triangle, "angle-angle-perimeter" is provided. Only following is directly constructed using the given parameters : a straight line, with length equivalent to the given perimeter. The given angles cannot be placed anywhere on the given straight line.
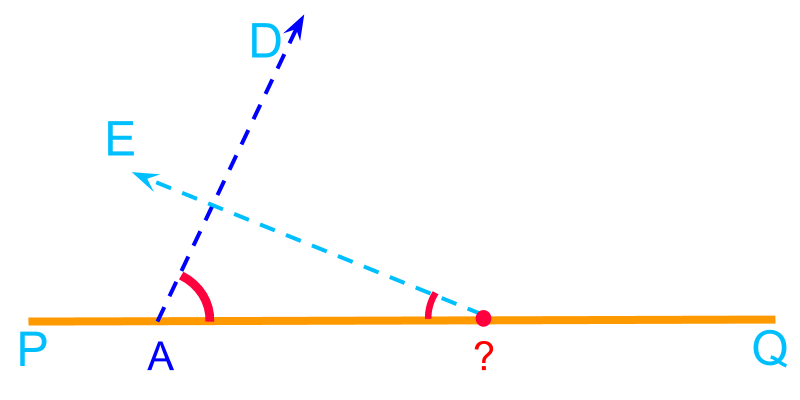
To construct a triangle with given "angle-angle-perimeter" , , and Perimetercm.
• Construct a line measuring cm
This is directly constructed from the given parameters.
Point is marked at an arbitrary position and locating or is constrained by the given two angles. The objective now is to locate the points and in the line and point such that the triangle has the given perimeter and the two angles.
• Construct a line measuring the perimeter cm.
• Point is visualized in an arbitrary position. It is not marked yet.
• From the point , the given angle is used to construct .
• The position of point is also visualized and the given angle is used to construct .
The point of intersection of and marks point .
In this procedure, the positions of and are not known.
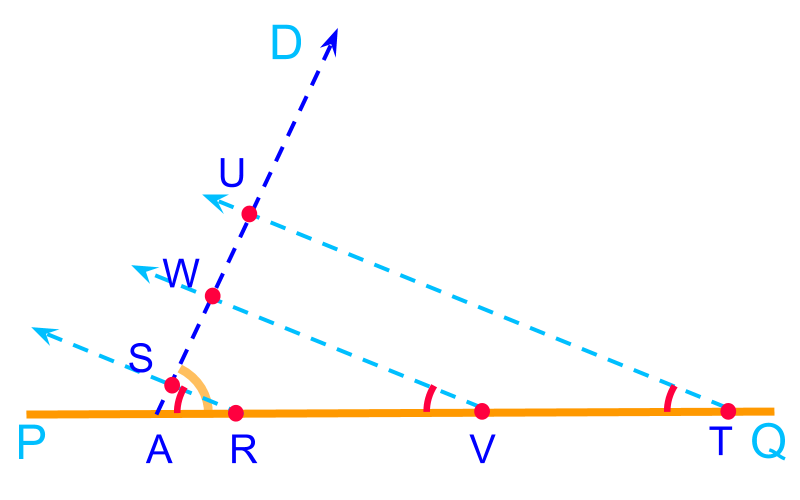
Consider rays , , and . All these rays are at the given angle . These rays make triangles , , and . These triangles have the given two angles. The following properties are noted for triangles and
• perimeter of is smaller than the given perimeter of triangle
• perimeter of is greater than the given perimeter of triangle
• It is noted that at only one position between the points and , the point is located such that perimeter of equals the given perimeter.
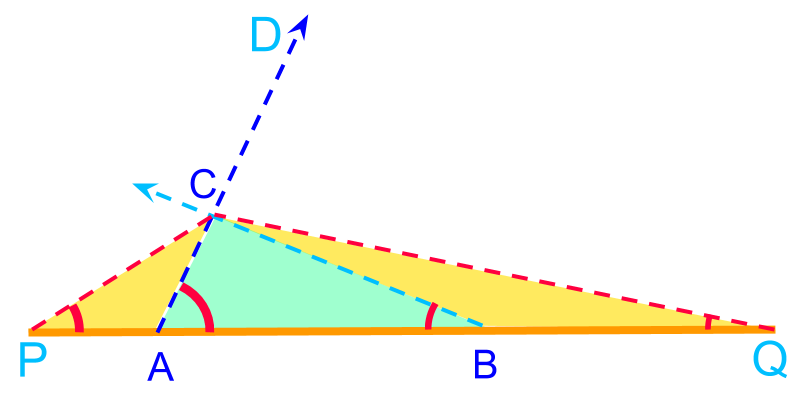
The points , , and are visualized such that the triangle satisfies the given perimeter and angles. The following are useful observations that will help to locate the point
• the line segments and are equal
• the line segments and are equal
• the triangles and are isosceles triangles
Additionally, the following is observed.
• the angle is half of the given angle
• the angle is half of the given angle
These will help to locate the point .
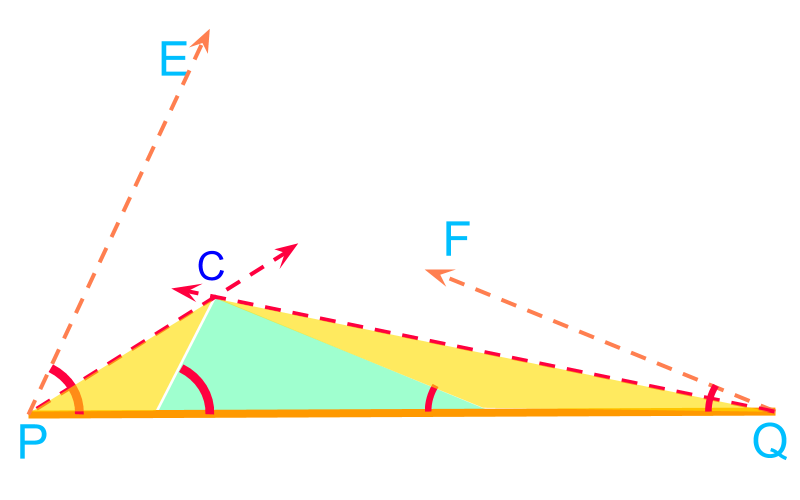
It is observed that
• and are isosceles
• the angle is half of the given angle
• the angle is half of the given angle
To construct the half angles at point and point , the given angles are constructed in and and bisected. The angle bisectors at and intersect at point

Using the property that
and are isosceles triangles
By copying an angle or by constructing perpendicular bisector on the base, the points and are marked.
is constructed.
summary

Construction of Angle-Angle-Perimeter of triangle : Visualize that at points , , and , and the are isosceles triangles.
Locate point by angle bisectors at point and .
Locate points and by either copying an angle or drawing perpendicular bisector on the base.
Outline
The outline of material to learn "Consrtruction (High school)" is as follows.
Note: Click here for detailed overview of "Consrtruction (High school)"
Note 2: click here for basics of construction, which is essential to understand this.
→ Construction of Triangles With Secondary Information
→ Construction: Scaling a line, triangle, polygon, circle
→ Construction of Tangents and Chord for a circle