Construction / Practical Geometry (High)
Welcome to the simple thought process to construction problems in practical geometry.
In the lesson on basics, the four fundamental elements of practical geometry is explained. And, the construction of various shapes using the fundamental elements is explained.
That is extended to the following.
• Construction of triangles using secondary information (sum of sides, difference of sides, and perimeter of sides).
• Scaling of lines, triangles, and other shapes.
• Consturction of elements of circle (tangents and chords)
The reasoning on how each of the procedures work is provided, which makes it easy for students to retain knowledge and work out the procedure.
maths > construction-high > construction-triangles-secondary-parameters
Construction of Triangles With Secondary Information
Triangles are defined by independent parameters. Usually, the three independent parameters are chosen from primary parameters -- the three sides and the three angles.
The sum of two sides, or perimeter of the triangle, etc. are secondary parameters.
If one or more of given parameters is of secondary type, then how to construct the specified triangle? A short overview of approaching such problems is provided in this lesson.
An overview of constructing triangles with angle-side-sum of two sides is provided. Sum of two sides is a secondary parameter.
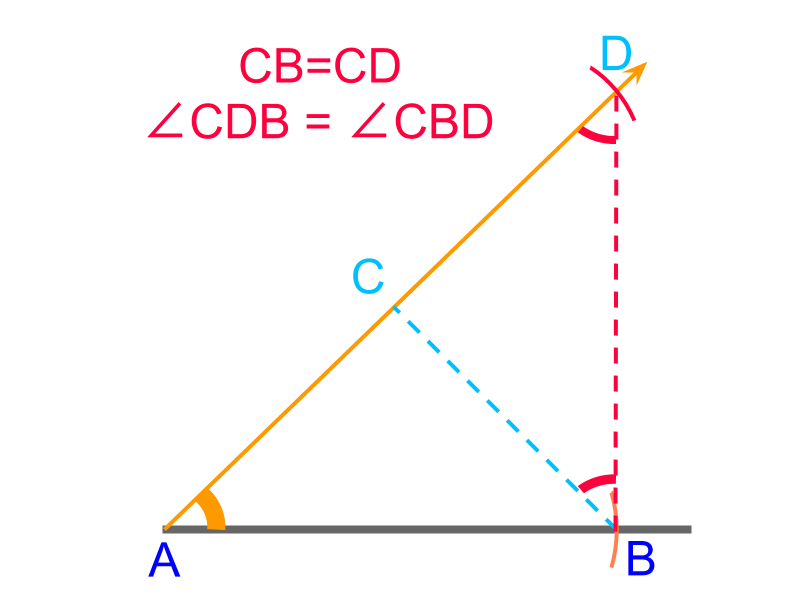
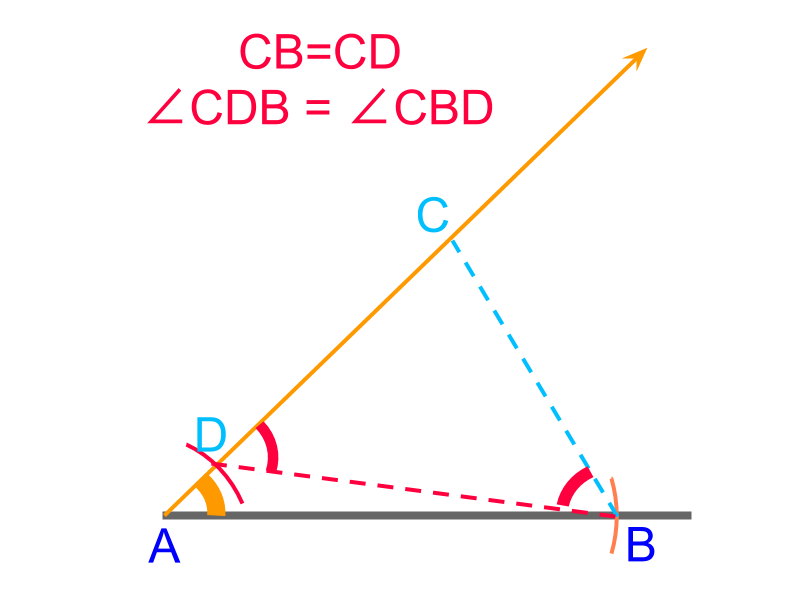
An overview of constructing triangles with angle-side-difference between two sides is provided. Difference between two sides is a secondary parameter.
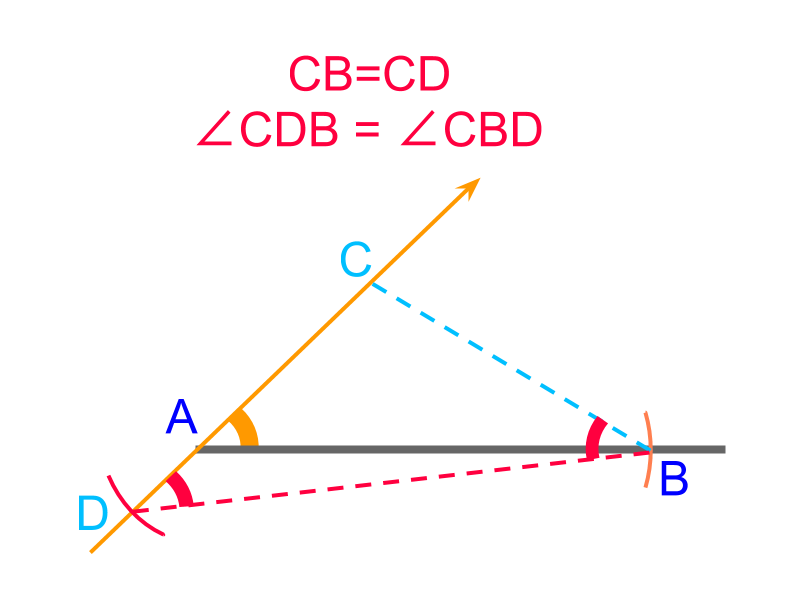
An overview of constructing triangles with angle-side-negative difference between two sides is provided. Negative difference between two sides is a secondary parameter.
An overview of constructing triangles with angle-angle-perimeter is provided. Perimeter is a secondary parameter.
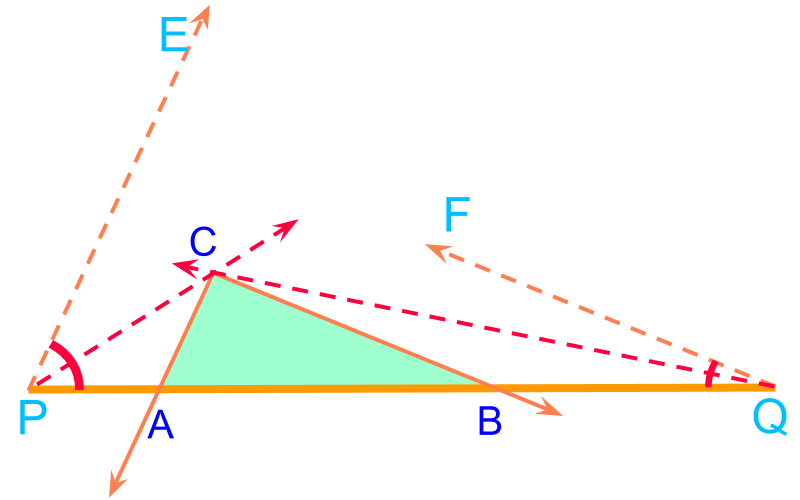
maths > construction-high > construction-scaling-line-triangle-polygons-circle
Construction: Scaling a line, triangle, polygon, circle
In this page, the following are covered
dividing a line in a given ratio (The method employed is based on properties of similar triangles.)
![]()
scaling or dividing a line in a given ratio (The method employed uses properties of traversal of pair of parallels.)
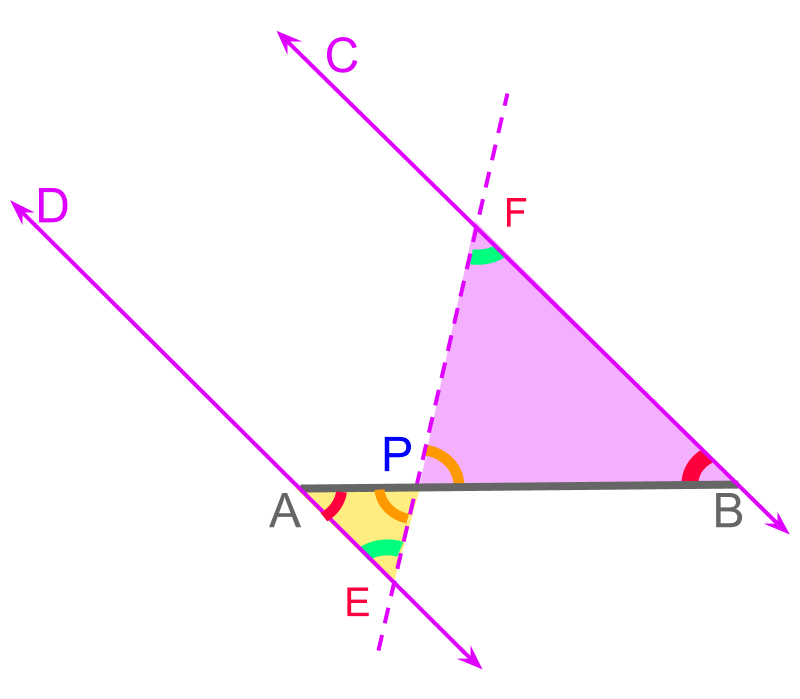
scaling a triangle in a given ratio

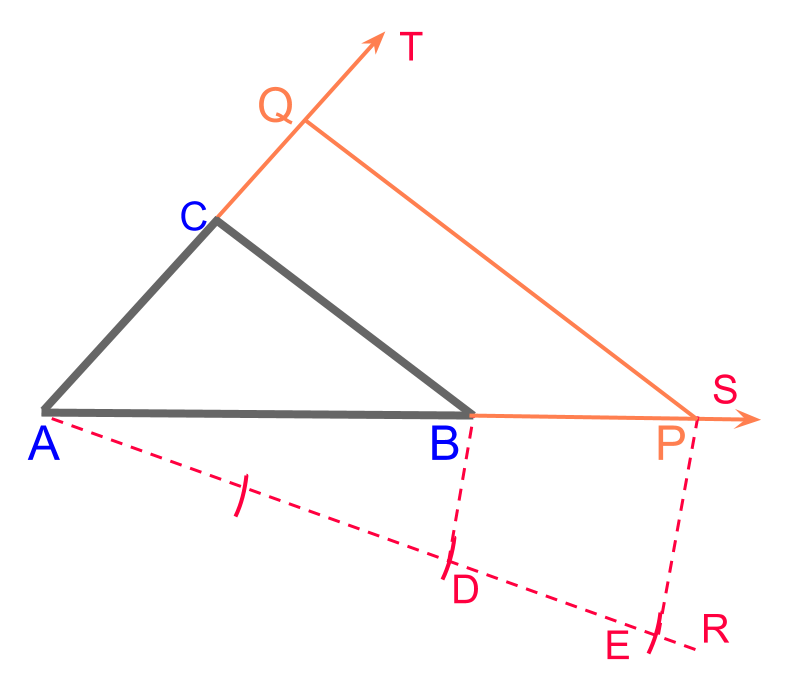
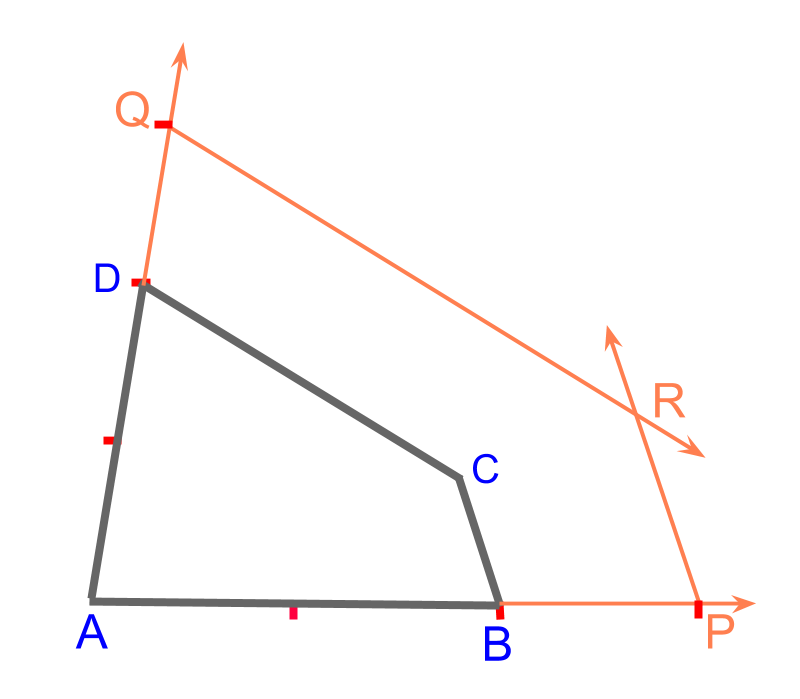
scaling a polygon in a given ratio
scaling a circle
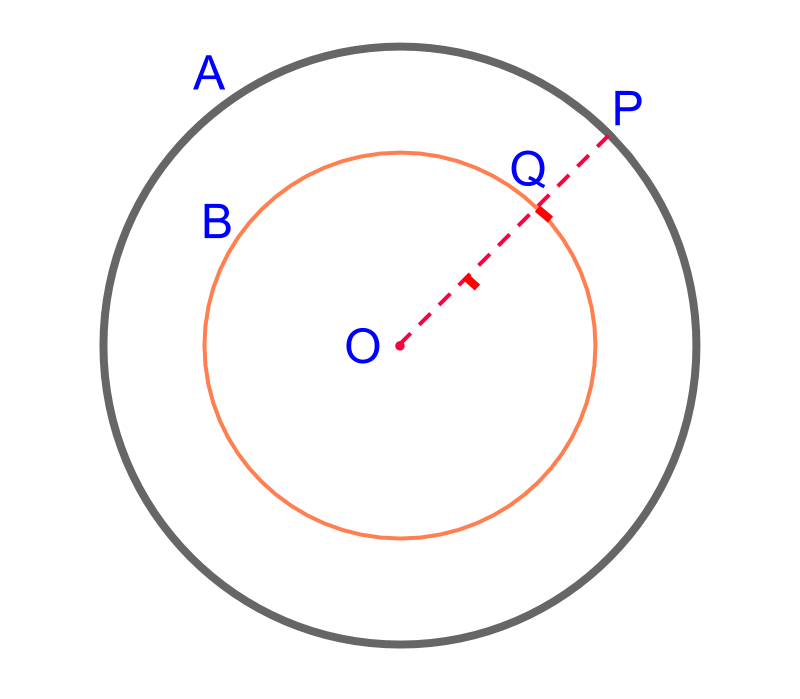
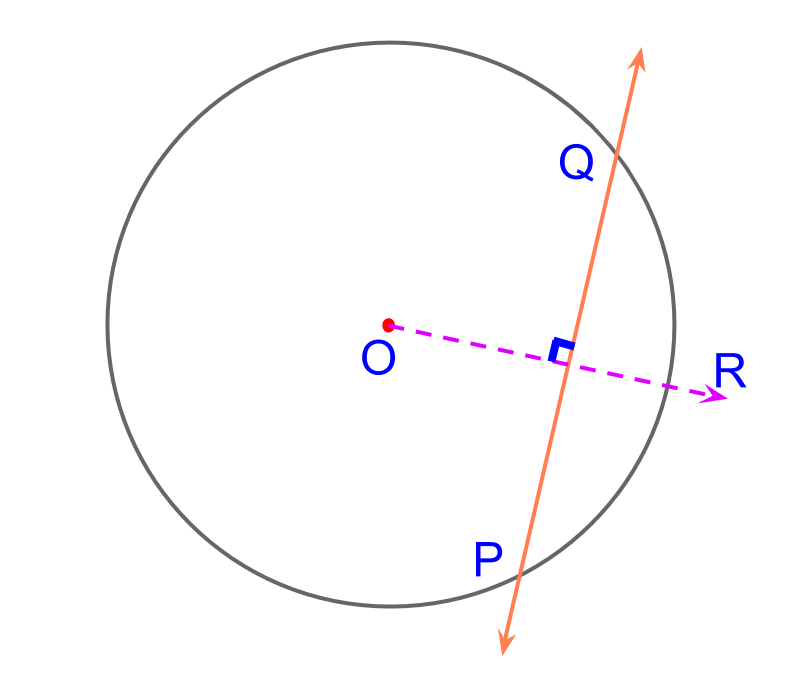
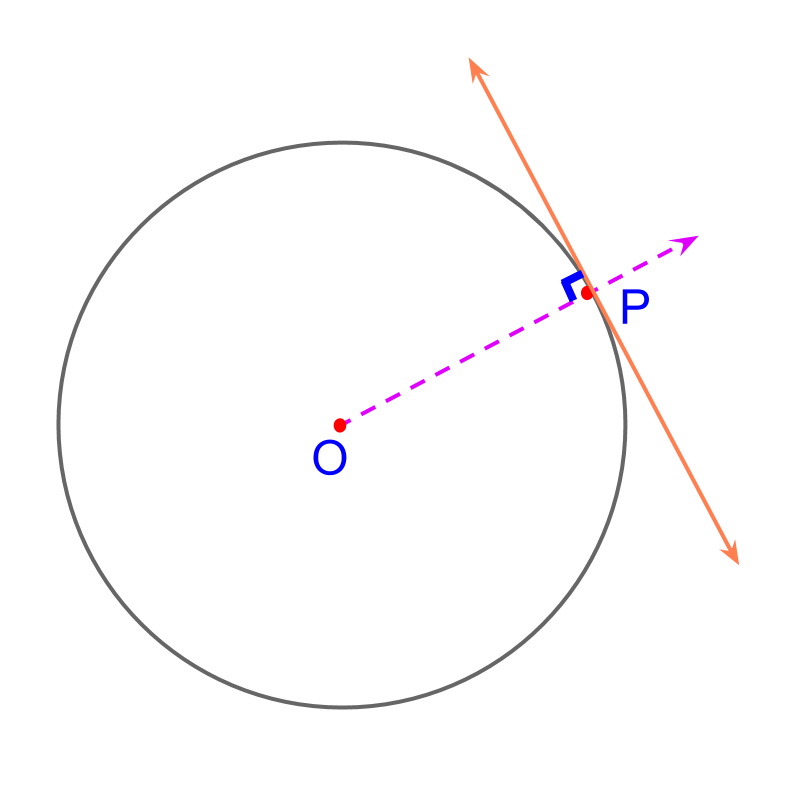
maths > construction-high > construction-tangent-chord-circle
Construction of Tangents and Chord for a Circle
In this page, a short overview of the following are provided.
• Construction of a Tangent on a Point on a Circle
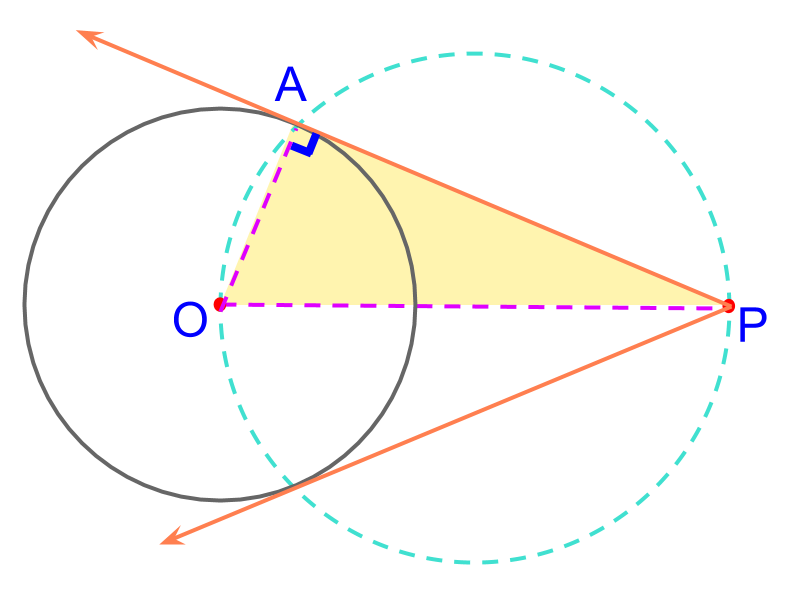
• Construction of Tangents from a Point outside a Circle
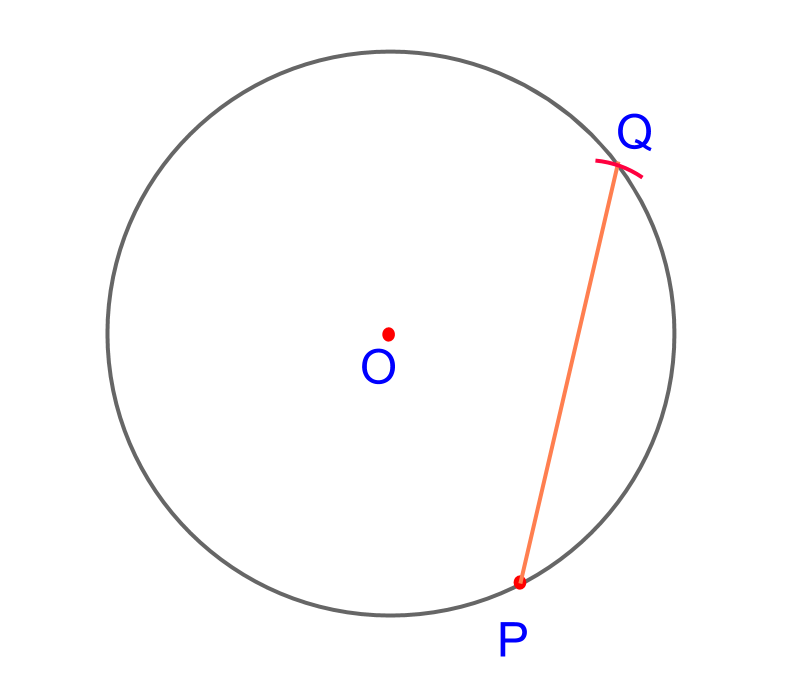
• Construction of chords of given length on a Circle
• Construction of chords at a given distance from center of a Circle