Construction / Practical Geometry (High) : Construction of Tangents and Chord for a Circle

maths > construction-high

Construction of Tangents and Chord for a Circle

what you'll learn...

overview

In this page, a short overview of the following are provided.

• Construction of a Tangent on a Point on a Circle Tangent on a point on circle
• Construction of Tangents from a Point outside a Circle Tangent on a point outside circle
• Construction of chords of given length on a Circle constructing a chord of a circle
• Construction of chords at a given distance from center of a Circle

tangent to a circle

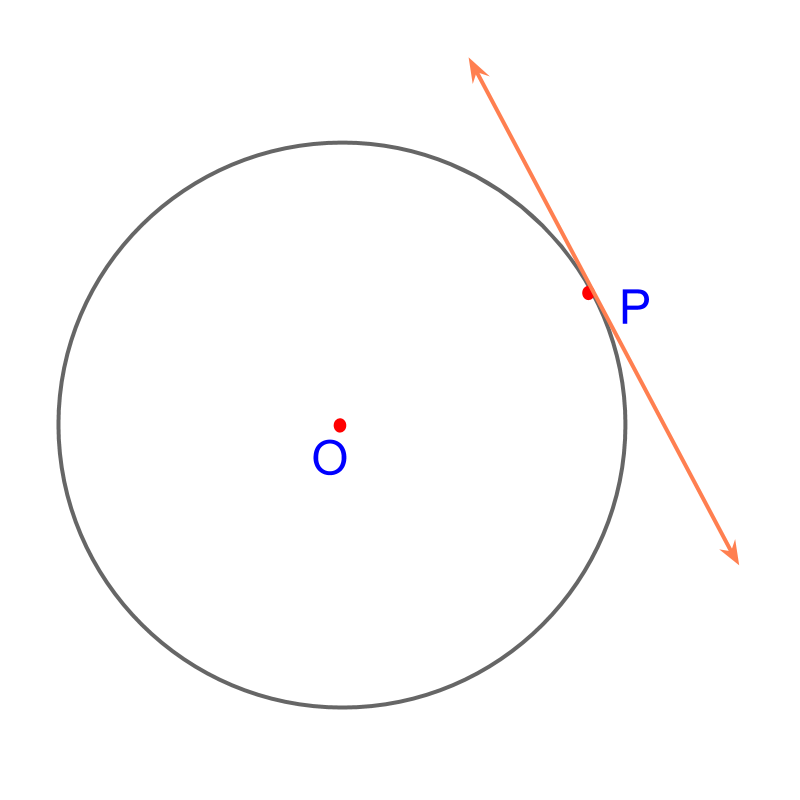
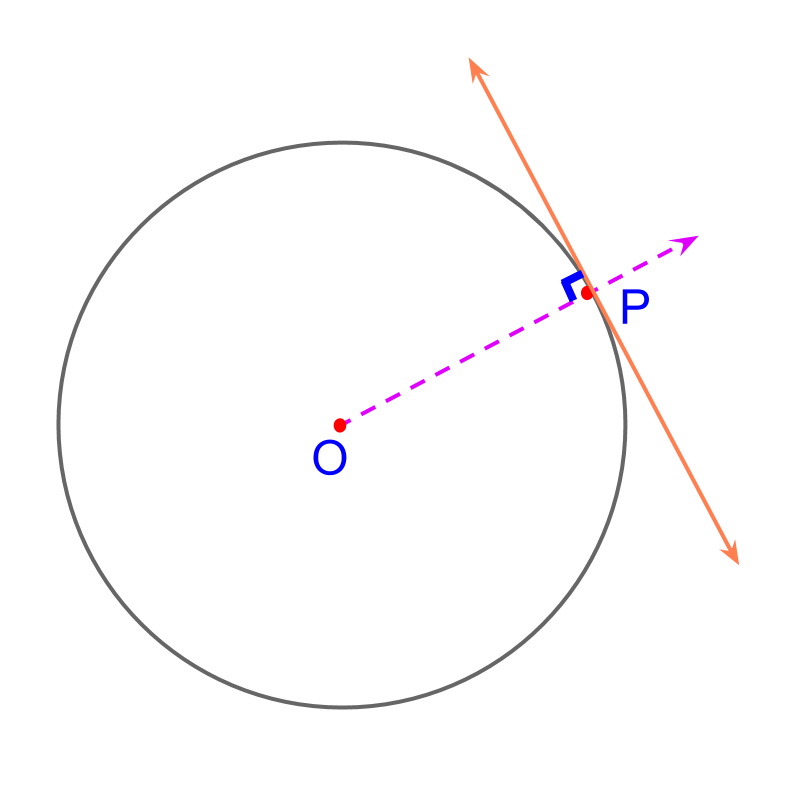
Consider the circle centered at $O$ $O$ . The objective is to construct a tangent on the given point $P$ $P$ on the circle.

To achieve that, we use the known property "tangent is at right angle $90^{\circ}$ $90^@$ to the radius at the point".

Considering the construction of tangent on the given point $P$ $P$ on a circle.

It is noted that the tangent is at right angle to the radius at the point. The ray $\vec{O P}$ $vec(OP)$ is constructed. Construct a perpendicular on point $P$ $P$ on the ray $\vec{O P}$ $vec(OP)$ . This construction problem is modified to the known problem : construction of a perpendicular on a point in a line.

The following steps detail construction of tangent on point $P$ $P$ on a circle:

• The ray $\vec{O P}$ $vec(OP)$ is constructed

• On the point $P$ $P$ , the perpendicular to $\vec{O P}$ $vec(OP)$ is constructed.
(Construction of a perpendicular on a point is explained in the earlier lessons)

The tangent is constructed.

summary

Construction of Tangent on a point on circle: Using the property that the radius and tangent on a point are at right angle, the construction is modified to construction of perpendicular to a line on a point.

tangent from outside

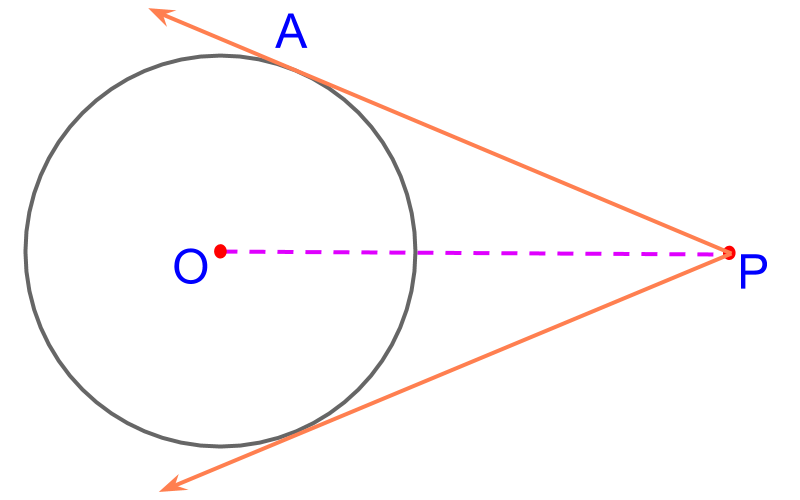
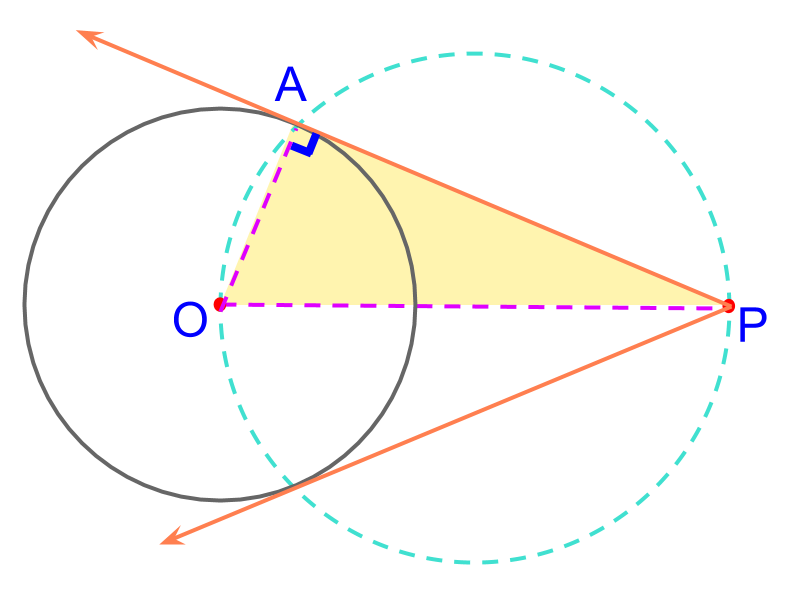
Consider the circle centered at $O$ $O$ . The objective is to construct a tangent from the given point $P$ $P$ outside the circle. To achieve that we use the property, tangent is at right angle $90^{\circ}$ $90^@$ to the radius at the point of tangent.

Considering the construction of tangent from the given point $P$ $P$ outside the circle.

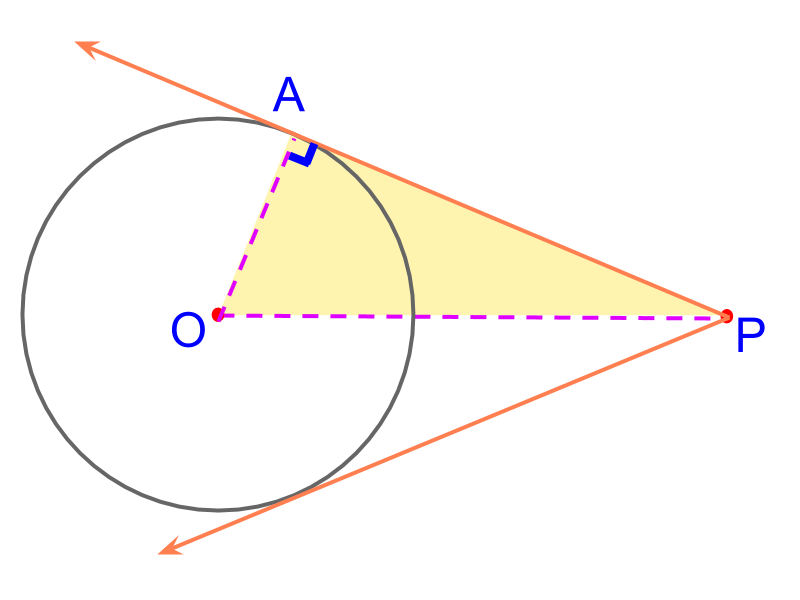
The point of tangent on the circle is visualized as point $A$ $A$ . It is shown in the figure to illustrate. The point $A$ $A$ is not yet marked. It is noted that $△ O A P$ $/_\OAP$ is a right angled triangle with $\bar{O P}$ $bar(OP)$ as the hypotenuse.

To mark the point $A$ $A$ , "constructing a circle with hypotenuse as diameter".

The point $A$ $A$ is not yet marked. It is noted that $△ O A P$ $/_\OAP$ is a right angled triangle with $\bar{O P}$ $bar(OP)$ as the hypotenuse.

The angle subtended by a diameter on the circle is right-angled.

Using this knowledge, It is visualized that a circle with diameter $\bar{O P}$ $bar(OP)$ intersects the given circle at point $A$ $A$ , where angle $∠ O A P$ $/_OAP$ is $90^{\circ}$ $90^@$ and so, $\vec{P A}$ $vec(PA)$ is the tangent at point $A$ $A$ .

The following steps detail construction of tangent from point $P$ $P$ outside a circle:

• The ray $\vec{O P}$ $vec(OP)$ is constructed

• A circle is constructed with $\bar{O P}$ $bar(OP)$ as the diameter.
(Construction of a circle with a given line segment as diameter is explained in the earlier lessons)

• The points of intersection of the given circle to the constructed circle are connected to $P$ $P$ as the tangents of the given circle.

The tangents are constructed.

summary

Construction of Tangents from a point outside a Circle : Note the following properties

• the radius and tangent are perpendicular,

• the angle subtended by diameter on a circle is right-angle

the line segment between the center of the circle and the given point is considered as diameter.

The construction is modified to construction of a circle on a given line segment as diameter.

chord of length

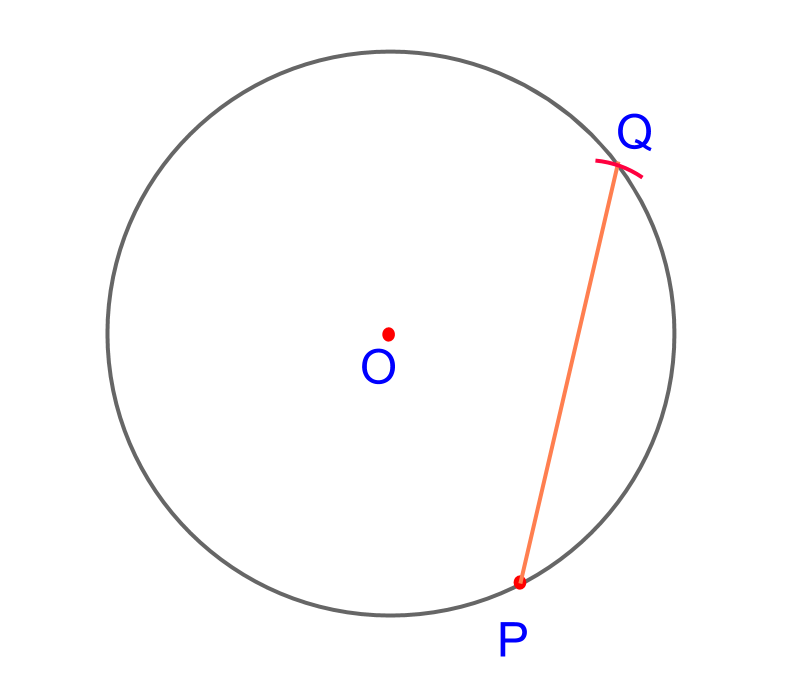
Consider the circle centered at $O$ $O$ . The objective is to construct a chord of length $\bar{P Q} = 4$ $bar(PQ) = 4$ cm on the given point $P$ $P$ on the circle.

To achieve that a compass is enough. A compass constructs equidistant points.

The following steps detail construction of chord at point $P$ $P$ on a circle:

• Use a compass to construct an arc of length $4$ $4$ cm.

• The point of intersection of the arc on the circle is marked $Q$ $Q$ .

• Connect the points $P$ $P$ and $Q$ $Q$

The chord $\bar{P Q}$ $bar(PQ)$ is constructed.

Note: There are two chords possible from the given point $P$ $P$ of the given length.

summary

Construction of Chords of given length : An arc of the given length is used to locate the points on circle and the chord is constructed.

chord at distance

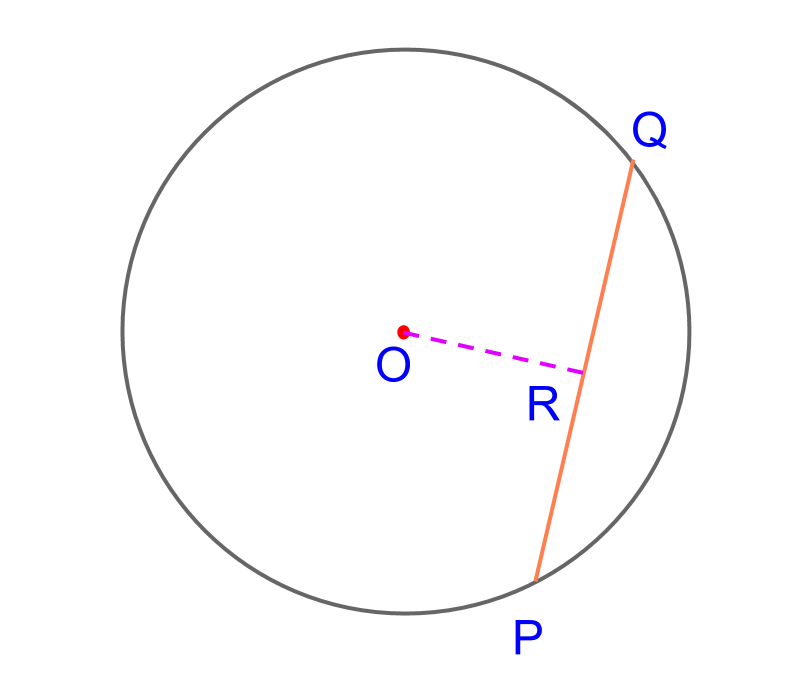
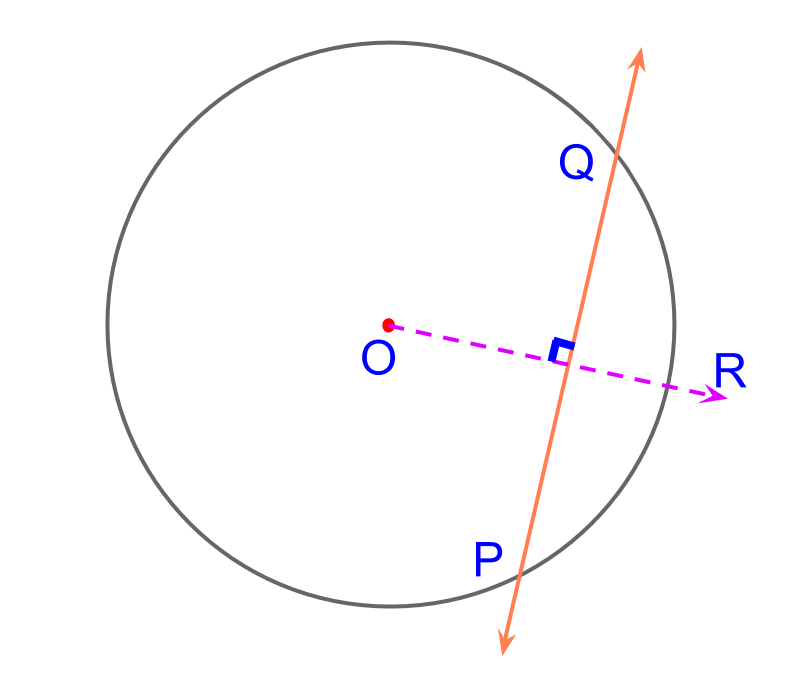
Consider the circle centered at $O$ $O$ . The objective is to construct a chord at $2$ $2$ cm distance from the center. To achieve that we use the definition : the distance of chord from the center is length of the perpendicular line from the center.

The following steps detail construction of chord at a distance:

• Construct a ray $\vec{O R}$ $vec(OR)$ .

• Using a compass, measure the given $2$ $2$ cm distance and mark on the ray $\vec{O R}$ $vec(OR)$ .

• At the point of intersection, construct a perpendicular $\vec{P Q}$ $vec(PQ)$

• The ray intersects at points $P$ $P$ and $Q$ $Q$

The chord $\bar{P Q}$ $bar(PQ)$ is constructed.

summary

Construction of Chord at a distance from Center of the circle : Using the property that the distance of a chord from the center is measured as the perpendicular distance, a perpendicular is constructed on a radius at the given distance.

Outline

The outline of material to learn "Consrtruction (High school)" is as follows.

Note: Click here for detailed overview of "Consrtruction (High school)"

Note 2: click here for basics of construction, which is essential to understand this.

→ Construction of Triangles With Secondary Information

→ Construction: Scaling a line, triangle, polygon, circle

→ Construction of Tangents and Chord for a circle