Construction / Practical Geometry (High) : Construction: Scaling a line, triangle, polygon, circle

maths > construction-high

Construction: Scaling a line, triangle, polygon, circle

what you'll learn...

overview

In this page, the following are covered

dividing a line in a given ratio (The method employed is based on properties of similar triangles.) dividing a line using similar triangles
scaling or dividing a line in a given ratio (The method employed uses properties of traversal of pair of parallels.) dividing a line using traversal of parallels
scaling a triangle in a given ratio scale-down a triangle scale-up a triangle
scaling a polygon in a given ratio scaling a quadrilateral
scaling a circle

problem

Given a line segment $\bar{A B}$ $bar(AB)$ , it is required to mark a point $P$ $P$ such that, $\bar{A P} : \bar{P B} = m : n$ $bar(AP):bar(PB) = m : n$ . That is, the $\bar{A B}$ $bar(AB)$ is divided to $\bar{A P}$ $bar(AP)$ and $\bar{P B}$ $bar(PB)$ in $m : n$ $m:n$ ratio.

To achieve that, we use properties of similar triangles.

A set of similar triangles are formed with $\bar{A B}$ $bar(AB)$ as one of its sides. The formulation is shown in the figure. In such a construction, the following properties are noted.

• $\bar{A B} : \bar{A P} = \bar{A D} : \bar{A C}$ $bar(AB) : bar(AP) = bar(AD) : bar(AC)$

• $\bar{E B} ∣ ∣ \bar{C P}$ $bar(EB) || bar(CP)$

The construction is explained in following pages.

The construction is visualized in the following.

• Construct a ray $\vec{A R}$ $vec(AR)$ at an angle, of any measurement.

• In a compass, take a measurement

• Using the compass, mark a number of segments on the ray.

• Construct line $D$ $D$ to $B$ $B$

• Construct a line through the the point $C$ $C$

• The point of intersection of the line through $C$ $C$ and $\bar{A B}$ $bar(AB)$ is marked $P$ $P$ .

The figure illustrates $3$ $3$ different angles $∠ A R 1$ $/_AR1$ , $∠ A R 2$ $/_AR2$ , and $∠ A R 3$ $/_AR3$ . The procedure to construct will work for any arbitrary measure of angle.

Continuing on dividing line segment $\bar{A B}$ $bar(AB)$ in ratio $\bar{A P} : \bar{P B} = 2 : 1$ $bar(AP):bar(PB)= 2:1$ . The construction is visualized in the following.

• Construct a ray $\vec{A R}$ $vec(AR)$ at an angle

• In a compass, take a measurement. Any arbitrary length will do fine.

• Using the compass, mark a number of segments on the ray.

• Construct line $D$ $D$ to $B$ $B$

• Construct a line through the the point $C$ $C$

• The point of intersection of line through $C$ $C$ and $\bar{A B}$ $bar(AB)$ is marked $P$ $P$ .

Continuing on dividing $\bar{A B}$ $bar(AB)$ in ratio $2 : 1$ $2:1$ . The figure illustrates $3$ $3$ different measures on compass. The procedure to construct will work for any arbitrary length.

Continuing on dividing line segment $\bar{A B}$ $bar(AB)$ in ratio $\bar{A P} : \bar{P B} = 2 : 1$ $bar(AP):bar(PB)= 2:1$ . The construction is visualized in the following.

• Construct a ray $\vec{A R}$ $vec(AR)$ at an angle

• In a compass, take a measurement

• Using the compass, mark a number of segments on the ray. To achieve $2 : 1$ $2:1$ , sum of $2$ $2$ and $1$ $1$ = $3$ $3$ segments are marked.,

• Construct line $D$ $D$ to $B$ $B$

• Construct a parallel to $\bar{D B}$ $bar(DB)$ through the the point $C$ $C$

• The point of intersection of parallel through $C$ $C$ and $\bar{A B}$ $bar(AB)$ is marked $P$ $P$ .

Continuing on dividing $\bar{A B}$ $bar(AB)$ in ratio $2 : 1$ $2:1$ . The lines through points $C 1$ $C1$ , $C 2$ $C2$ , and $C 3$ $C3$ are parallel to $\bar{D 1 B}$ $bar(D1B)$ , $\bar{D 2 B}$ $bar(D2B)$ , and $\bar{D 3 B}$ $bar(D3B)$ respectively. By the rules of similar triangles, the lines intersect at point $P$ $P$ .

The construction is visualized in the following.

• Construct a ray $\vec{A R}$ $vec(AR)$ at an angle

• In a compass, take a measurement

• Using the compass, mark a number of segments on the ray.

• Construct line $D$ $D$ to $B$ $B$

• Construct a parallel to $\bar{D B}$ $bar(DB)$ through the point $C$ $C$

• The point of intersection of the parallel through $C$ $C$ and $\bar{A B}$ $bar(AB)$ is marked $P$ $P$ .

The ratio $\bar{A P} : \bar{P B}$ $bar(AP):bar(PB)$ is same as the ratio $\bar{A C} : \bar{C D}$ $bar(AC):bar(CD)$ , which is $2 : 1$ $2:1$

summary

Segmenting a line in a given ratio (Triangle Method): Use the property of similar triangles the given line can be segmented. Given $\bar{A B}$ $bar(AB)$ to be divided in ratio $m : n$ $m:n$ .

The triangle $△ A B D$ $/_\ABD$ is constructed with $\bar{A D}$ $bar(AD)$ having $m + n$ $m+n$ segments. By using the first $m$ $m$ segments, the similar triangle $△ A C P$ $/_\ACP$ is created.

Since, $\bar{A C} : \bar{C D}$ $bar(AC):bar(CD)$ is $m : n$ $m:n$ , by the similarity property of triangle, $\bar{A P} : \bar{P B} = m : n$ $bar(AP):bar(PB)=m:n$

segmenting a line

The objective is to divide the given line $\bar{A B}$ $bar(AB)$ in ratio $m : n$ $m:n$ . The properties of similar triangles help in acheiving that.

dividing a line using traversal of parallels

A set of similar triangles are formed with $\bar{A B}$ $bar(AB)$ and a pair of parallel lines. The formulation is shown in the figure. In such a construction, the following properties are noted.

• $\bar{A D} ∣ ∣ \bar{B C}$ $bar(AD) || bar(BC)$

• $\bar{A P} : \bar{A E} = \bar{P B} : \bar{B F}$ $bar(AP) : bar(AE) = bar(PB) : bar(BF)$

The construction is explained in the following pages.

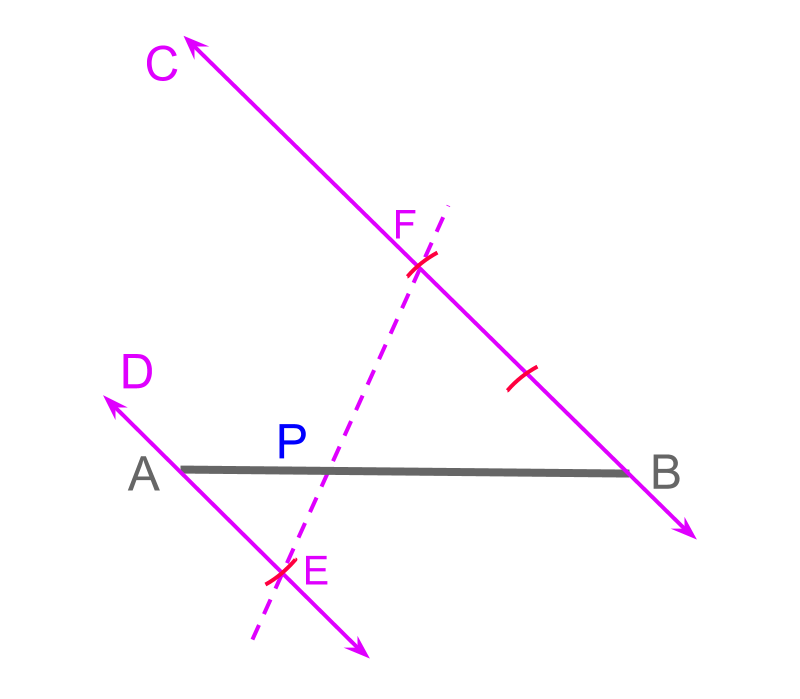
The objective is to divide the given line $\bar{A B}$ $bar(AB)$ in ratio $\bar{A P} : \bar{P B} = 1 : 2$ $bar(AP):bar(PB)= 1:2$ .

The construction is visualized in the following.

• Construct a ray $\vec{B C}$ $vec(BC)$ at an angle. Any angles will do fine.

• Construct another ray $\vec{A D}$ $vec(AD)$ in parallel to $\vec{B C}$ $vec(BC)$ .

• In a compass, take a measurement. Any arbitrary length will do fine.

• Using the compass, mark a number of segments on the rays $\vec{A D}$ $vec(AD)$ and $\vec{B C}$ $vec(BC)$ marking points $E$ $E$ and $F$ $F$ .

• Construct line $E$ $E$ to $F$ $F$

• The point $P$ $P$ is marked at the intersection of $\bar{E F}$ $bar(EF)$ and $\bar{A B}$ $bar(AB)$ .

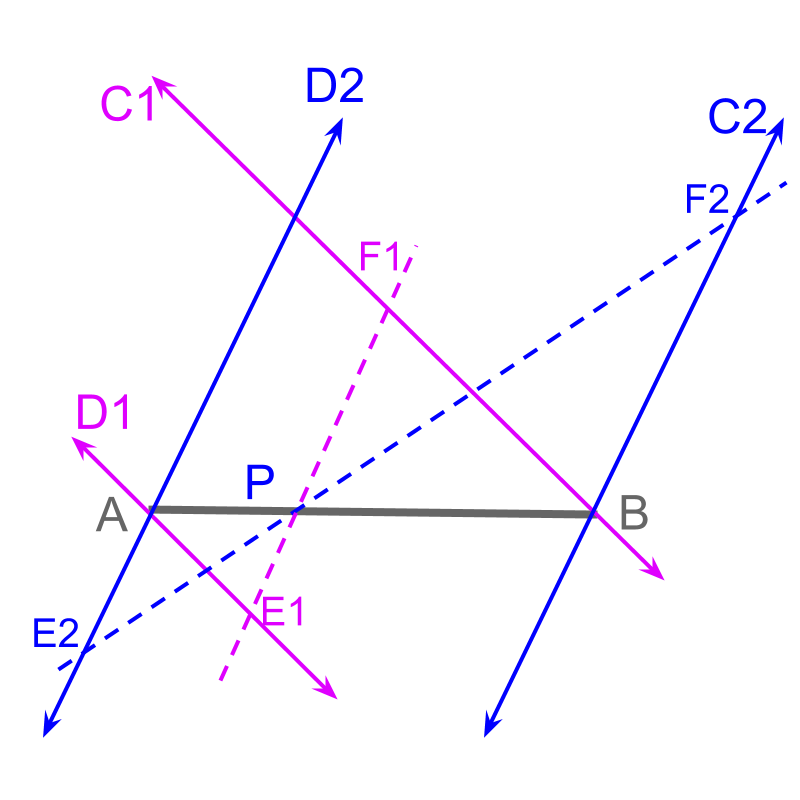
The figure illustrates $3$ $3$ different angles. The procedure will work for any arbitrary measure of angle.

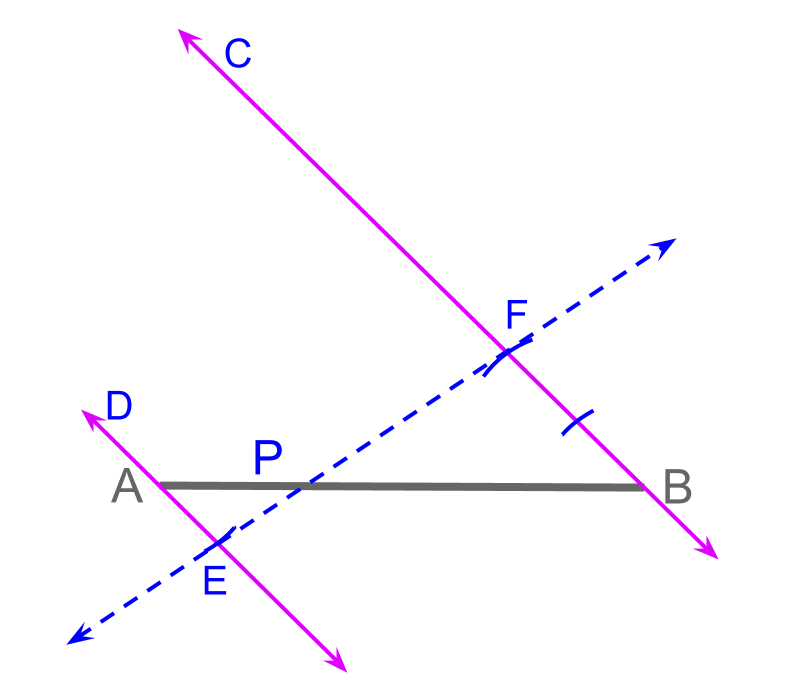
The construction is visualized as given below.

• Construct a ray $\vec{B C}$ $vec(BC)$ at an angle

• Construct another ray $\vec{A D}$ $vec(AD)$ in parallel to the $\vec{B C}$ $vec(BC)$ .

• In a compass, take an arbitrary length on the compass

• Using the compass, mark a number of segments on the rays $\vec{A D}$ $vec(AD)$ and $\vec{B C}$ $vec(BC)$ marking points $E$ $E$ and $F$ $F$ .

• Construct line $E$ $E$ to $F$ $F$

• The point $P$ $P$ is marked at the intersection of $\bar{E F}$ $bar(EF)$ and $\bar{A B}$ $bar(AB)$ .

The figure illustrates $3$ $3$ different measures on compass $\bar{A E 1}$ $bar(AE1)$ , $\bar{A E 2}$ $bar(AE2)$ , $\bar{A E 3}$ $bar(AE3)$ . The procedure to construct will work for any arbitrary length.

Continuing on dividing $\bar{A B}$ $bar(AB)$ in ratio $\bar{A P} : \bar{P B} = 1 : 2$ $bar(AP):bar(PB)= 1:2$ .

• Using the measure on the compass, mark a number of segments on the rays $\vec{A D}$ $vec(AD)$ and $\vec{B C}$ $vec(BC)$ marking points $E$ $E$ and $F$ $F$ . To achieve $1 : 2$ $1:2$ ratio, the points are marked with $1$ $1$ segment on $\vec{A D}$ $vec(AD)$ and $2$ $2$ segments on $\vec{B C}$ $vec(BC)$

From the properties of similar trianges, $\bar{A P} : \bar{P B} = 1 : 2$ $bar(AP):bar(PB)= 1:2$ , same as the ratio $\bar{A E} : \bar{B F}$ $bar(AE):bar(BF)$ .

summary

Segmenting a line in a given Ratio (Traversal of pair of parallels) : Use the properties of angles in the traversal of parallel lines and the similar triangles, the given line can be segmented. Given $\bar{A B}$ $bar(AB)$ to be divided in ratio $m : n$ $m:n$ .

The parallels $\vec{A D}$ $vec(AD)$ and $\vec{B C}$ $vec(BC)$ are constructed.

Mark points $E$ $E$ and $F$ $F$ in the given ratio $m : n$ $m:n$ . Since $\bar{A E} : \bar{B F}$ $bar(AE):bar(BF)$ is in the given ratio $m : n$ $m:n$ , by the similarity property of triangles, $\bar{A P} : \bar{P B} = m : n$ $bar(AP):bar(PB)=m:n$

scale-down a triangle

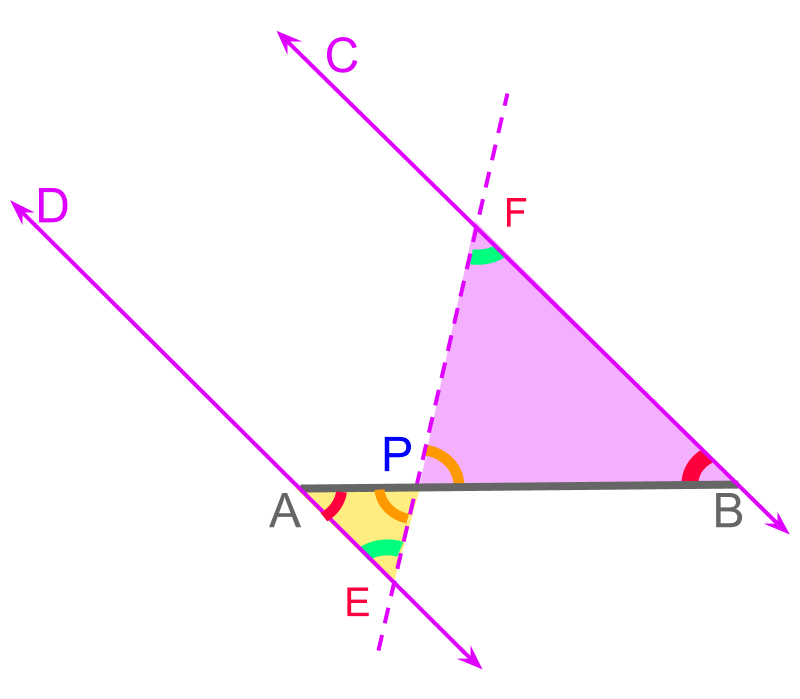
Consider the given $△ A B C$ $/_\ABC$ . The objective is to construct $△ A P Q$ $/_\APQ$ such that the corresponding sides are in ratio $3 : 2$ $3:2$ . To achieve that, the first step is to divide the side $\bar{A B}$ $bar(AB)$ to mark point $P$ $P$ . Then $\bar{P Q}$ $bar(PQ)$ can be constructed to complete $△ A P Q$ $/_\APQ$ .

Considering scaling the given $△ A B C$ $/_\ABC$ to $△ A P Q$ $/_\APQ$ in the ratio $3 : 2$ $3:2$ . The given ratio is for the corresponding sides of the triangles, i.e. $\bar{A B} : \bar{A P}$ $bar(AB):bar(AP)$ . But to divide the $\bar{A B}$ $bar(AB)$ , the ratio is modified to $\bar{A P} : \bar{P B} = 2 : 1$ $bar(AP):bar(PB) = 2:1$ .

Considering scaling the given $△ A B C$ $/_\ABC$ to $△ A P Q$ $/_\APQ$ in the ratio $3 : 2$ $3:2$ . The figure illustrates the solution. The $\bar{A B}$ $bar(AB)$ is segmented to $\bar{A P}$ $bar(AP)$ and $\bar{P B}$ $bar(PB)$ . This marks the point $P$ $P$ .

To mark $Q$ $Q$ , construct the line $\bar{P Q}$ $bar(PQ)$ in parallel to $\bar{B C}$ $bar(BC)$ .

summary

Scaling a Triangle:The figure illustrates the solution. The $\bar{A B}$ $bar(AB)$ is segmented to $\bar{A P}$ $bar(AP)$ and $\bar{P B}$ $bar(PB)$ . This marks the point $P$ $P$ .

The $\bar{P Q}$ $bar(PQ)$ is constructed in parallel to $\bar{B C}$ $bar(BC)$ .

$△ A P Q$ $/_\APQ$ is constructed.

scale-up a triangle

Consider the given $△ A B C$ $/_\ABC$ . The objective is to construct $△ A P Q$ $/_\APQ$ such that the corresponding sides are in the ratio $2 : 3$ $2:3$ . To achieve that, one of the sides can be scaled-up to construct similar triangles.

Scale-up the side $\bar{A B}$ $bar(AB)$ to mark point $P$ $P$ ;. Then $\bar{P Q}$ $bar(PQ)$ can be constructed to complete $△ A P Q$ $/_\APQ$ .

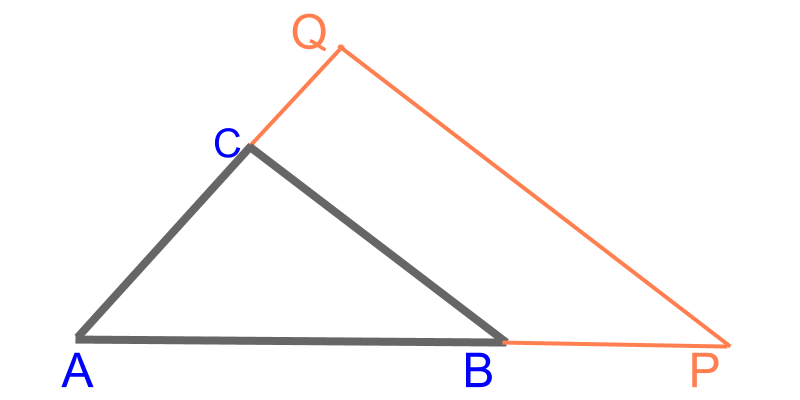
Considering scaling the given $△ A B C$ $/_\ABC$ to $△ A P Q$ $/_\APQ$ in the ratio $2 : 3$ $2:3$ . The given ratio is for the corresponding sides of the triangles, i.e. $\bar{A B} : \bar{A P}$ $bar(AB):bar(AP)$ . But to scale the $\bar{A B}$ $bar(AB)$ , the ratio is modified to $\bar{A B} : \bar{B P} = 2 : 1$ $bar(AB):bar(BP) = 2:1$ .

The figure illustrates the solution. The $\bar{A B}$ $bar(AB)$ is scaled to $\bar{A B}$ $bar(AB)$ and $\bar{B P}$ $bar(BP)$ . This marks the point $P$ $P$ . To mark $Q$ $Q$ , construct the line $\bar{P Q}$ $bar(PQ)$ in parallel to $\bar{B C}$ $bar(BC)$ and extend $\bar{A C}$ $bar(AC)$ .

The figure illustrates the solution. The $\bar{A B}$ $bar(AB)$ is scaled up to $\bar{A B}$ $bar(AB)$ and $\bar{B P}$ $bar(BP)$ . This marks the point $P$ $P$ .

The $\bar{A C}$ $bar(AC)$ is extended to the ray $\vec{A T}$ $vec(AT)$ . The $\bar{P Q}$ $bar(PQ)$ is constructed in parallel to $\bar{B C}$ $bar(BC)$ and that meets $\vec{A T}$ $vec(AT)$ .

$△ A P Q$ $/_\APQ$ is constructed.

summary

Scaling of Triangles : To scale a triangle, scale one of the sides and use the properties of similar triangles to construct the scaled triangle.

scaling quadrilateral

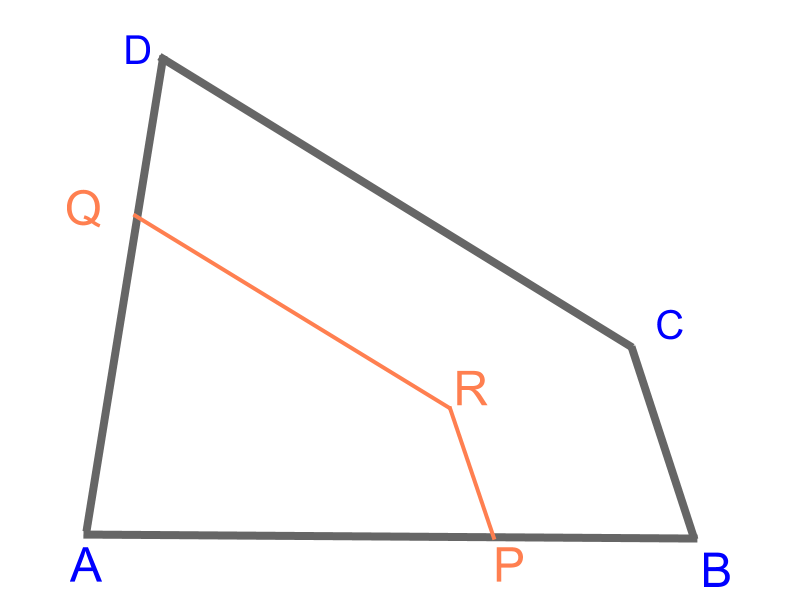
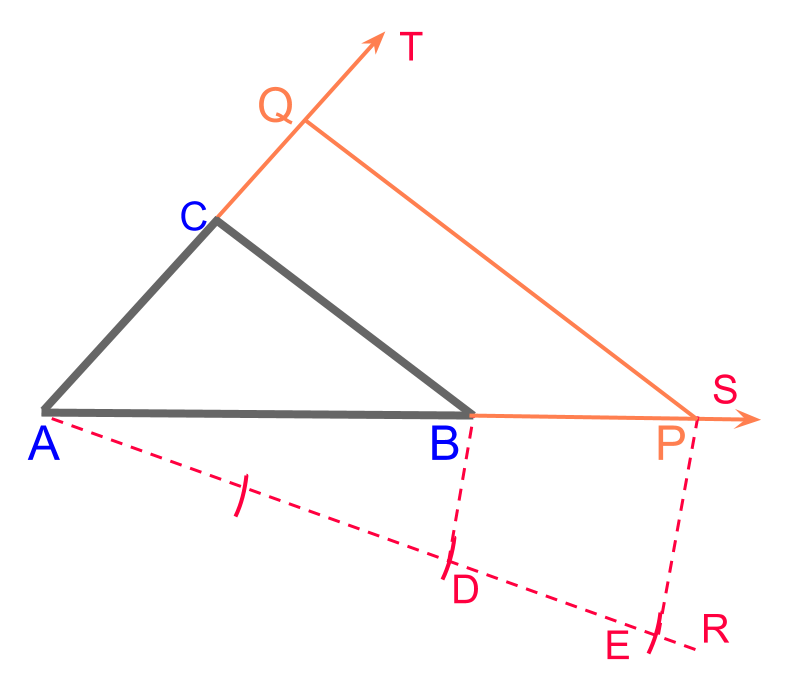
Consider the given quadrilateral $A B C D$ $ABCD$ . The objective is to construct the quadrilateral $A P R Q$ $APRQ$ such that the corresponding sides are in ratio $3 : 2$ $3:2$ . To achieve that, divide the sides, to mark points $P$ $P$ and $Q$ $Q$ and construct parallels to mark point $R$ $R$ .

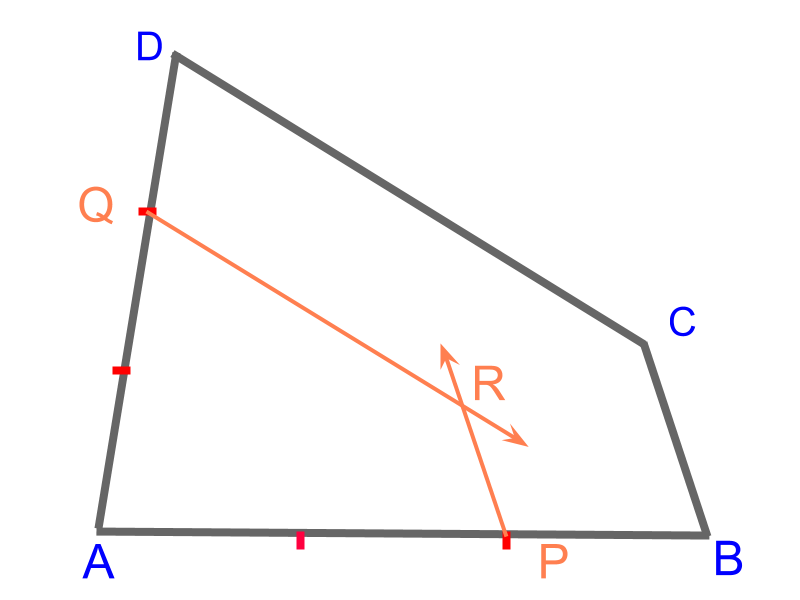
Consider the given quadrilateral $A B C D$ $ABCD$ . The objective is to construct the quadrilateral $A P R Q$ $APRQ$ such that the corresponding sides are in ratio $3 : 2$ $3:2$ .

The following steps details construction of the quadrilateral $A P R Q$ $APRQ$ .

• Divide the side $A B$ $AB$ to $2 : 1$ $2:1$ ratio to mark point $P$ $P$ .

• Divide the side $A D$ $AD$ to $2 : 1$ $2:1$ ratio to mark point $Q$ $Q$ .

• Construct two rays $\vec{P R}$ $vec(PR)$ and $\vec{Q R}$ $vec(QR)$ in parallel to $\bar{B C}$ $bar(BC)$ and $\bar{D C}$ $bar(DC)$ respectively.

• The point of intersection is point $R$ $R$ .

Quadrilateral $A P R Q$ $APRQ$ is constructed.

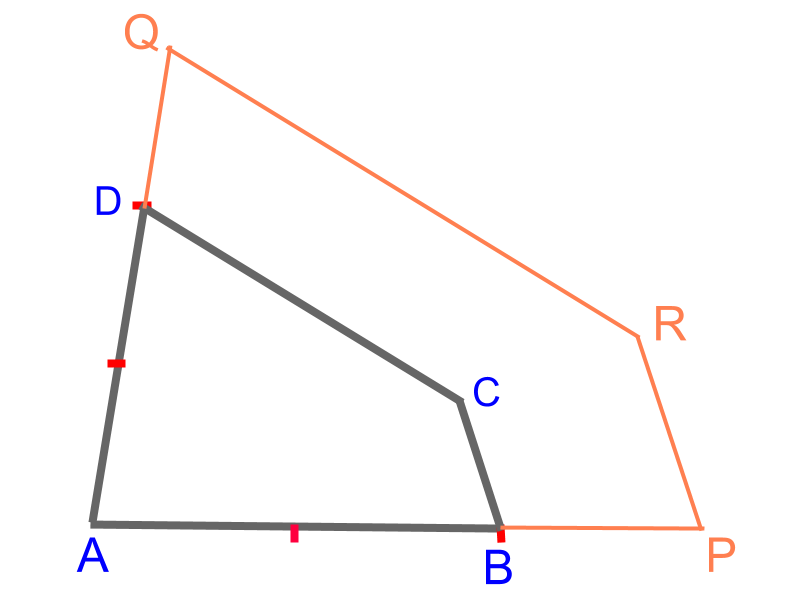
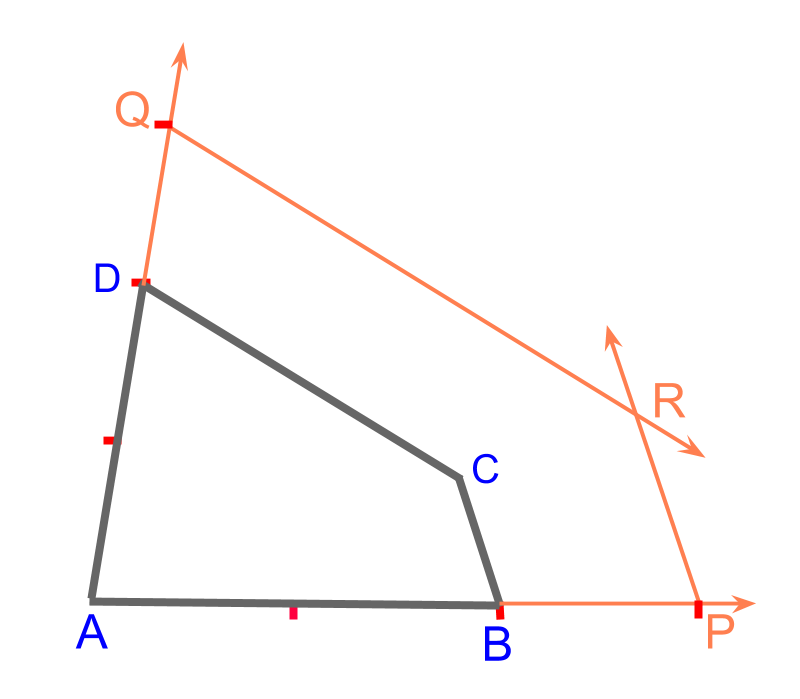
Consider the given quadrilateral $A B C D$ $ABCD$ . The objective is to construct the quadrilateral $A P R Q$ $APRQ$ such that the corresponding sides are in ratio $2 : 3$ $2:3$ . To achieve that scale-up the sides, to mark points $P$ $P$ and $Q$ $Q$ and construct parallels to mark point $R$ $R$

Consider the given quadrilateral $A B C D$ $ABCD$ . The objective is to construct the quadrilateral $A P R Q$ $APRQ$ such that the corresponding sides are in ratio $2 : 3$ $2:3$

The following steps details construction of the quadrilateral $A P R Q$ $APRQ$ .

• Scale-up the side $A B$ $AB$ to $2 : 1$ $2:1$ ratio to mark point $P$ $P$ .

• Scale-up the side $A D$ $AD$ to $2 : 1$ $2:1$ ratio to mark point $Q$ $Q$ .

• Construct two rays $\vec{P R}$ $vec(PR)$ and $\vec{Q R}$ $vec(QR)$ in parallel to $\bar{B C}$ $bar(BC)$ and $\bar{D C}$ $bar(DC)$ respectively.

• The point of intersection is point $R$ $R$

Quadrilateral $A P R Q$ $APRQ$ is constructed.

summary

Scaling of Polygons : To scale a polygon, scale a side and construct a parallel to the next side and scale the side in the parallel. Continue this with all the sides to complete scaling the given polygon.

scaling a circle

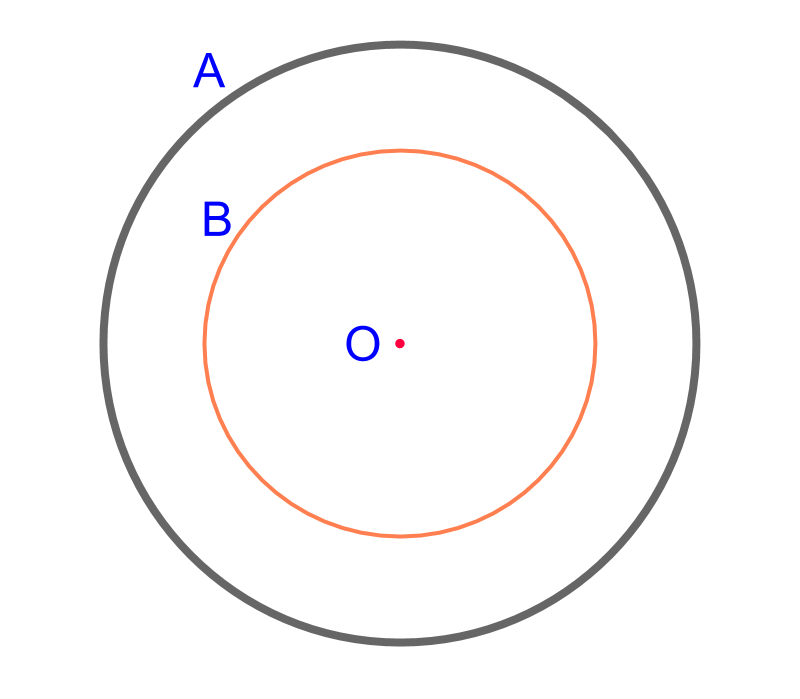
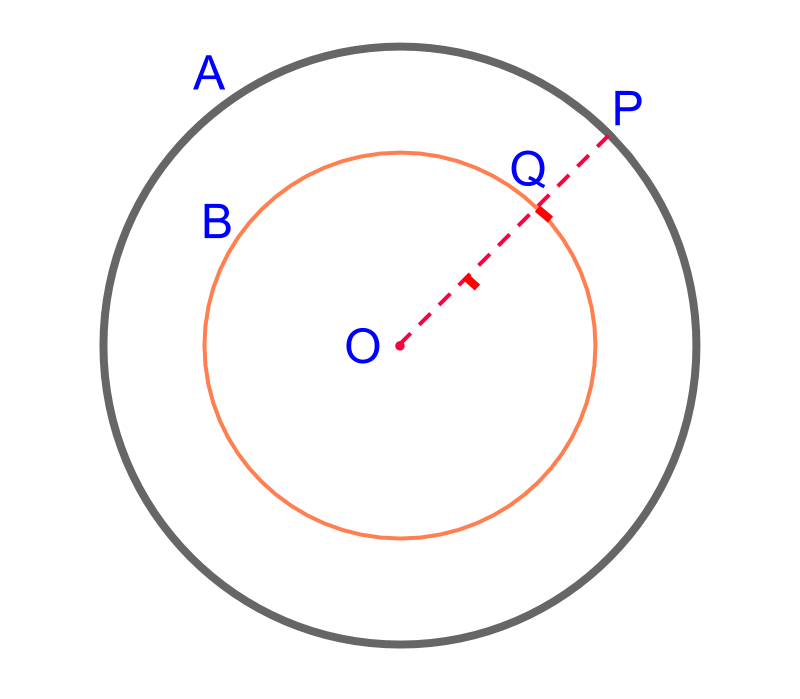
Consider the given circle $A$ $A$ centered at point $O$ $O$ . The objective is to construct circle $B$ $B$ such that the radius are in ratio $3 : 2$ $3:2$ . To achieve that, construct a radius and divide it in $2 : 1$ $2:1$ ratio

Consider the given circle $A$ $A$ centered at point $O$ $O$ . The objective is to construct circle $B$ $B$ such that the radius are in ratio $3 : 2$ $3:2$

The following steps detail scaling a circle.

• Construct a radius $\bar{O P}$ $bar(OP)$ .

• Scale the radius in ratio $2 : 1$ $2:1$ to mark point $Q$ $Q$ .

• Construct a circle with radius $\bar{O Q}$ $bar(OQ)$ . Scaled Circle $B$ $B$ is constructed.

summary

Scaling a Circle : To scale a circle, scale a radius as per scaling a line segment. The scaled circle is constructed with scaled line segment as the radius.

Outline

The outline of material to learn "Consrtruction (High school)" is as follows.

Note: Click here for detailed overview of "Consrtruction (High school)"

Note 2: click here for basics of construction, which is essential to understand this.

→ Construction of Triangles With Secondary Information

→ Construction: Scaling a line, triangle, polygon, circle

→ Construction of Tangents and Chord for a circle