Divisibility in Whole Numbers : Simple Divisibility Tests

maths > wholedivisors

Simple Divisibility Tests

what you'll learn...

overview

This page covers the following

• the divisibility test for $2$ $2$

• the divisibility test for $10$ $10$

• the divisibility test for $3$ $3$

• the divisibility test for $4$ $4$

• the divisibility test for $5$ $5$

• the divisibility test for $11$ $11$

• the divisibility test for $9$

• the divisibility test for $6$

Divisibility by 2

Consider the multiples of $2$ given as $2,4,6,8,10,12, cdots$ . A similarity is observed in the multiples -- they are all even numbers.

Let us consider the numbers $4$ and $5$ .
The even number $4$ is divisible by $2$ . But the odd number $5$ is not divisible by $2$ .

Even numbers are divisible by $2$ . To check for divisibility by $2$ , only the digit in the units place is checked.

Test for Divisibility by $2$ : If the digit in the units place is even, then the number is divisible by $2$ .

Is $218$ divisible by $2$ ?
"Yes". Checking the digit in units place $8$ , it is concluded that the number is even and so divisible by $2$ .

Is $23$ divisible by $2$ ?
"No". Checking the digit in units place $3$ , it is concluded that the number is odd and so NOT divisible by $2$ .

Divisibility by 10

Consider the multiples of $10$ given as $10,20,30,40,cdots$ . A similarity is observed in the multiples -- "they all have digit $0$ in the units place". That is, all multiples of $10$ end in $0$ .

Numbers with $0$ in units place are divisible by $10$ .

Consider the numbers $20$ and $24$ . Checking the units place, $20$ has $0$ and so $20$ is divisible by $10$ . But $24$ has $4$ in units place, and so $24$ is not divisible by 10.

Test for Divisibility by $10$ : If the digit in the units place is $0$ , then the number is divisible by $10$ .

Is $2008$ divisible by $10$ ?
"No". Checking the digit in units place $8$ , it is concluded that the number is not divisible by $10$ .

Is $920$ divisible by $10$ ?
"Yes". Checking the digit in units place $0$ , it is concluded that the number is divisible by $10$ .

Divisibility by 3

" $3,6,9,12,15,18,21,24,27,30,33, cdots$ " are the multiples of $3$ . From the list, it is not easy to find a common property among the multiples.

Consider the multiples of $3$ given as $3,6,9,12,15,18,21,24,27,30,33, cdots$ . The similarity is "sum of all digits is one of the numbers $3, 6, 9$ ".

This is explained as follows
$12 -> 1+2=3$ sum is $3$
$15 -> 1+5=6$ sum is $6$
$18 -> 1+8=9$ sum is $9$
$21 -> 2+1=3$ sum is $3$
$24 -> 2+4=6$ sum is $6$
$27 -> 2+7=9$ sum is $9$

The property is true for all multiples of $3$ .

To identify the multiplies of $3$ , the sum of all digits of the number is checked for divisibility by $3$ .

Explanation for the curious mind.

Consider divisibility test $42$ by $3$

To simplify the divisibility test, let us subtract a multiple of the divisor $3$ .
Seeing the $10$ s place value $4$ , we choose the multiple $3xx3xx4 = 36$ to subtract from the number.

As per the property of simplification by subtraction, the divisibility test of $42$ is simplified into divisibility test of $42-36 = 40-36+2 = 4+2$ .

This explains the divisibility test for $3$ .

Consider the numbers $12$ and $13$ .
$12 -> 1+2=3$ sum $3$ is divisible by 3, so $12$ is divisible by $3.$
$13 -> 1+3=4$ sum $4$ is not divisible by 3, so $13$ is not divisible by $3.$

Test for Divisibility by 3 : If the sum of all the digits is divisible by $3$ then the number is divisible by $3$

Is $318$ divisible by $3$ ?
Yes. Checking the sum of digits $3+1+8=12$ . The sum is divisible by $3$ . It is concluded that the number is divisible by $3$ .

Is $923$ divisible by $3$ ?
No. Checking sum of the digits $9+2+3 = 14$ , it is concluded that the number is NOT divisible by $3$ .

Divisibility by 4

The multiples of $4$ have the property that last two digits are divisible by $4$ .

Explanation for the curious mind

A large number like $2344$ can be given as $23xx100+44$ .

It was learned that if one addend is divisible, then the divisibility is decided by the other addend.

$23xx100$ is always divisible by $4$ as $100=25xx4$ .

So, the divisibility test is done in $44$ , that is the tens and units digits.

Test for Divisibility by 4 : If the last $2$ digits (tens and units place value positions) of the number is divisible by $4$ then the number is divisible by $4$ .

Is $2018$ divisible by $4$ ?
No. Checking the tens and units digits $18$ , it is concluded that the number is not divisible by $4$ .

Is $920$ divisible by $4$ ?
Yes. Checking the tens and units digits $20$ , it is concluded that the number is divisible by $4$ .

Divisibility by 5

the multiples of $5$ are $5,10,15,20,25, cdots$ . The multiples of $5$ has either $5$ or $0$ in the units place. The divisibility test for $5$ is to check if the units digit is either $5$ or $0$ .

Explanation for the curious mind

A large number like $2344$ can be given as $234xx10+4$ .

It was learned that if one addend is divisible, then the divisibility is decided by the other addend.

$234xx10$ is divisible by $5$ as $10=5xx2$ .

So, the divisibility test is done on the last digit, that is the units digits. In the units digit the possible values are $5$ and $0$ .

Consider $10$ and $25$ . Both $10$ and $25$ are divisible by $5$
$10$ has $0$ in units place. So, $10$ is divisible by $5$ .
$25$ has $5$ in units place. So, $25$ is divisible by $5$ .

Test for Divisibility by $5$ : If the units digit is $5$ or $0$ , then the number is divisible by $5$ .

Is $2018$ divisible by $5$ ?
No. Checking the digit in units place $8$ , it is concluded that the number is not divisible by $5$ .

Is $920$ divisible by $5$ ?
Yes. Checking the digit in units place $0$ , it is concluded that the number is divisible by $5$ .

Divisibility by 11

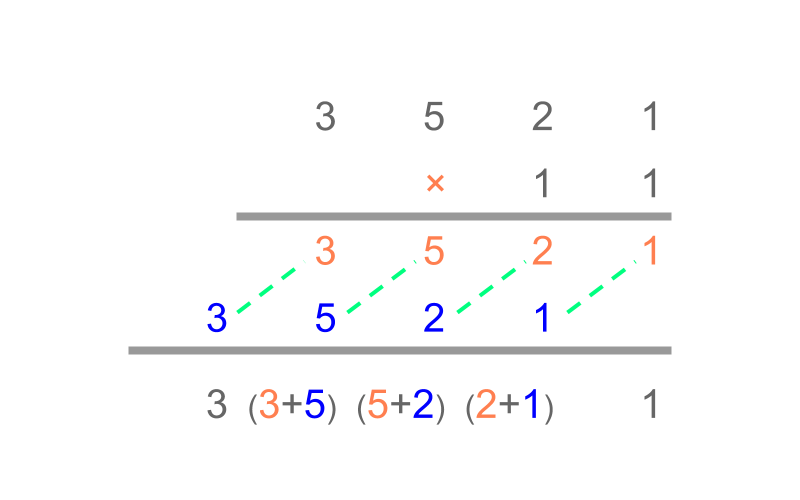
Consider the multiples of $11$ given as $11,22,33, cdots, 110,121,132, cdots$ . Is there any similarity observed in the multiples?
The answer is "alternate digits have some pattern".

"Note: A number $3521$ when multiplied by $11$ is given as

$3521 xx 11$
$=3521 xx(10+1)$
$=35210+ 3521$
$=(3)(5+3)(2+5)(1+2)(1)$

Four digit number, when multiplied by $11$ , results in
• units digit of product is same as that of multiplicand
• tens digit of product is sum of units and tens digit of multiplicand
• hundreds digit of product is sum of tens and hundreds digit of multiplicand
• and so on.
We can use this property to device a divisibility test for $11$ .

The multiples of $11$ have the property explained below. For example, consider $121$ (a multiple of $11$ ).

Add the digits in odd positions $1+1$ , the result is $2$
Add the digits in even positions $2$ .
Find the difference between these two results.
If the difference is $0$ or a multiple of $11$ , then the number is a divisible by $11$ .

Test for Divisibility by 11 : Find the sum of digits in even positions and the sum of digits in odd positions. If the difference between these two sums is a multiple of 11, then the number is divisible by 11.

Is $2108$ divisible by $11$ ?
No. The sum of alternate digits are $2+0=2$ and $1+8=9$ . The difference between these sums are $9-2 = 7$ . Since $7$ is not divisible by $11$ , the number is not divisible by $11$ .

Is $902$ divisible by $11$ ?
Yes. The $9+2-0 = 11$ , so the number is divisible by $11$ .

Divisibility by 9

Consider the multiples of $9$ given as $9,18,27,36, cdots$ . A similarity is observed in these multiples : "sum of all digits is a multiple of $9$ ".

This is explained as follows
$18 -> 1+8=9$ sum is $9$
$27 -> 2+7=9$ sum is $9$
$36 -> 3+6=9$ sum is $9$
$189 -> 1+8+9=18$ sum is multiple of $9$

This is true for all multiples of $9$ .

To identify the multiplies of $9$ , the sum of all digits of the number is checked for divisibility by $9$ .

Explanation for the curious mind.

Consider divisibility test $42$ by $9$

To simplify the divisibility test, let us subtract a multiple of the divisor $9$ .
Seeing the $10$ s place value $4$ , we choose the multiple $9xx4$ to subtract from the number.

As per the property of simplification by subtraction, the divisibility test of $42$ is simplified into divisibility test of $42-36 = 40-36+2 = 4+2$ .

This explains the divisibility test for $9$ .

Test for Divisibility by $9$ : If the sum of all the digits is divisible by $9$ , then the number is divisible by $9$

Is $2008$ divisible by $9$ ?
No. Checking the sum of digits $2+0+0+8=10$ , it is concluded that the number is not divisible by $9$ .

Is $927$ divisible by $9$ ?
Yes. Checking the sum of digits $9+2+7=18$ , it is concluded that the number is divisible by $9$ .

Divisibility by 6

Consider the number $3xx2xx2351$ , is it divisible by $6$ ?
Yes, it is divisible by $6$ as it has $3$ and $2$ as factors.

Test for Divisibility by $6$ : If the number is divisible by $2$ and divisible by $3$ then the number is divisible by $6$

Is $2008$ divisible by $6$ ?
No. The number is divisible by $2$ but not by $3$ . So it is not divisible by $6$ .

Is $912$ divisible by $6$ ?
Yes. The number is divisible by $2$ and also divisible by $3$ . So it is divisible by $6$ .

summary

Test for Divisibility by $2$ : If the digit in the units place is even, then the number is divisible by $2$ .

Test for Divisibility by $10$ : If the digit in the units place is $0$ , then the number is divisible by $10$ .

Test for Divisibility by 3 : If the sum of all the digits is divisible by $3$ then the number is divisible by $3$

Test for Divisibility by 4 : If the last $2$ digits (tens and units place value positions) of the number is divisible by $4$ then the number is divisible by $4$ .

Test for Divisibility by $5$ : If the units digit is $5$ or $0$ , then the number is divisible by $5$ .

Test for Divisibility by 11 : Find the sum of digits in even positions and the sum of digits in odd positions. If the difference between these two sums is a multiple of 11, then the number is divisible by 11.

Test for Divisibility by $9$ : If the sum of all the digits is divisible by $9$ , then the number is divisible by $9$

Test for Divisibility by $6$ : If the number is divisible by $2$ and divisible by $3$ then the number is divisible by $6$

Outline

The outline of material to learn "Divisibility in Whole Numbers" is as follows.

Note: click here for detailed outline of Whole divisors

→ Classification as odd, even, prime, and composite

→ Factors, Multiples, Prime factorization

→ Highest Common Factor

→ Lowest Common Multiple

→ Introduction to divisibility tests

→ Simple Divisibility Tests

→ Simplification of Divisibility Tests

→ Simplification in Digits for Divisibility Tests