Divisibility in Whole Numbers : Simplification of Divisibility Tests

maths > wholedivisors

Simplification of Divisibility Tests

what you'll learn...

overview

The following are explained

• Simplification of divisibility test by subtraction

• Simplification of divisibility test by division

• Simplification of divisibility test by factors

These are used to develop other divisibility tests for specific numbers.

• the divisibility test for $8$ $8$

• the divisibility test for $12$ $12$

• the divisibility test for $15$ $15$

Divisibility: Simplification by Subtraction

Consider the problem : Given a number $83 \times 2322 = 192726$ $83xx2322 = 192726$ . is it divisible by $83$ $83$ ?
The solution is simple. The number is given as a multiple of $83$ $83$ , so it is divisible by $83$ .

Consider another number $83xx23 + 422 = 2331$ , Knowing that left addend $83xx23$ is divisible by $83$ , we can check the smaller number $422$ for divisibility which is easier.
That is, checking $422$ for divisibility is good enough to conclude divisibility of the number $2331$

If only the number $2331$ is given, then it can be simplified to a smaller number $2331-83xx20=671$ which is easier to deal with for divisibility test.

To check the divisibility, the following properties are helpful.

• multiple of a number is divisible by the number.
eg: $3xx423$ is a multiple of $3$ and so it is divisible by $3$ .

• In a sum of two numbers, if one number is a multiple of the divisor, then only the other number is checked for divisibility.
eg: Divisibility test of $3xx423 + 7$ by $3$ , can be simplified to divisibility test of $7$ , as $3xx423$ is a multiple of $3$ .

• To check divisibility of a large number by a divisor, it can be simplified into a smaller number by subtracting a multiple of the divisor.
eg: Divisibility test of $913$ by $3$ , can be simplified to divisibility test of $913-300xx3 = 13$

The method is named Simplification by Subtraction method.

Find the divisibility of $777012$ by $111$ .
Not Divisible. Subtract $777012 - 111xx7000 = 12$ . Check the divisibility of $12$

Find the divisibility of $804$ by $67$ .
Divisible. $134=67xx2$ is divisible by $67$

Divisibility: Simplification by Division

Given a number $340$ . is it divisible by $21$ ?
$340-210=130$ and $130$ is not divisible by $21$ . So, the number $340$ is not divisible by $21$

Consider divisibility of $340$ by $21$ .

An observation is that the dividend is an even number and the divisor is not. The dividend can be written as $2xx170$ .

The divisibility test can be performed on $170$ as the factor $2$ is a co-prime of $21$ .
This can further be simplified as $170-:2-:5 = 17$ , as $2$ and $5$ are co-primes of $21$ .

To check the divisibility of a composite dividend by a divisor, the factors of the dividend can help in simplifying the divisibility test.

• If a factor of dividend is co-prime of divisor, then the dividend can be divided by the co-prime factor and the divisibility test can be performed on the result.

This is named as Simplification by Division.

Simplification by Division: Dividend can be divided by a factor, that is co-prime of divisor, and the result is checked for divisibility.

Check divisibility of $990$ by $13$
$10$ and $9$ are co-primes of $13$ . So the number is divided as $990-:90 = 11$ . The result $11$ is not divisible by $13$ . So $990$ is not divisible by $13$ .

Divisibility: Simplification by Factors

Given a number $2321$ . Is it divisible by $58$ ?
$2321-58xx4 = 1$ . So, the number is not divisible by $58$

Consider the divisibility of dividend $2321$ by $58$ .
An observation is that if a number is multiple of divisor $58$ , then the number can be written as $58 xx n$ . The same can be written as $2xx29xxn$ , because $58=2xx29$ .

This implies that "the dividend is a multiple of $2$ and $29$ ". Since $2321$ is an odd number, it is not divisible by $2$ and so it is not divisible by $58$ .

Consider the divisibility of $922$ by $58$ .
It is observed that both are even numbers. So $922 = 2 xx 461$ and $58=2xx29$ .

This implies that "the factor $461$ should be a multiple of $29$ for the divisibility test to pass". That is divisibility test of $922$ by $58$ is now changed to divisibility test of $461$ by $29$ . The common factor $2$ is removed to simplify.

To check the divisibility of a dividend by a composite divisor, the factors of the divisors can help in simplifying the divisibility.

• If the dividend is not divisible by a factor of divisor, then the dividend is not divisible by the composite divisor.
eg: divisibility of $2321$ by $58$ . $58 = 2xx 29$ . The dividend $2321$ is not divisible by a factor of divisor $2$ , so $2321$ is not divisible by $58$ .

• If the dividend is divisible by a factor, then both the dividend and divisor can be divided by the factor and the test is done on the results.
eg: Divisibility of $922$ by $58$ . Both has common factor $2$ and so it is simplified as divisibility of $461$ by $29$ . This is named as Simplification by Factors.

Simplification by Factors: To simplify divisibility test of dividend by a divisor,

• any common factors can be removed from both the numbers and divisibility test can be performed on simplified dividend by the simplified divisor.

• the dividend has to have all the factors of the divisor to pass the divisibility test.

Check divisibility of $2016$ by $264$
The answer is "Not divisible"
The figure shows a simplified procedure by which simplification by factors can be performed.

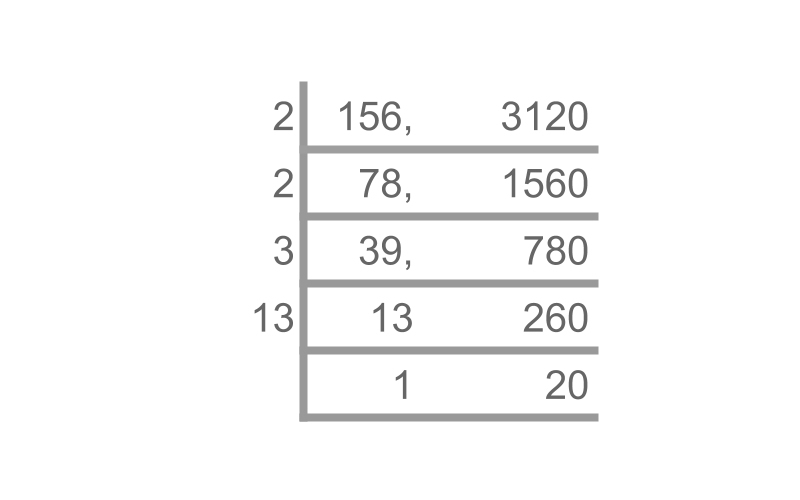
Check divisibility of $3120$ by $156$
The answer is "Divisible".
The figure shows the simplified procedure by which simplification by factors is performed.

Divisibility by 8

The multiples of $8$ have the property that lowest $3$ digits (hundreds, tens and units) is divisible by $8$ .

Explanation for the curious mind
A large number $2344$ can be given in the form $2xx1000+344$ .
It is learned that if one addend is divisible, then the divisibility test can be performed only on the second addend.
$2xx1000$ is divisible by $8$ as $1000=125xx8$ .
So the divisibility test is performed on $344$ , that is the last $3$ digits of the number.

Test for Divisibility by $8$ : If the last three digits of the dividend is divisible by $8$ , then the dividend is divisible by $8$ .

Is $2018$ divisible by $8$ ?
Checking the last three digits $18$ . As $18$ is not a multiple of $8$ , it is concluded that the number is not divisible by $8$ .

Is $7120$ divisible by $8$ ?
Checking the last three digits $120$ . As $120$ is a multiple of $8$ , it is concluded that the number is divisible by $8$ .

Is $73524$ divisible by $8$ ?
Checking the last three digits $524$ . The divisibility test can be simplified by subtraction ( $524-400-80-40$ ) or simplified by factors ( $(524,8)$ simplified to $(262,4)$ , then to $(131,2)$ ).

Divisibility by 12

If a number is given as $3xx4xx2351$ , will it be divisible by $12$ ?
It is divisible by $12$ as it has $3$ and $4$ as factors"

Test for Divisibility by $12$ : If a number is divisible by $3$ and $4$ , then the number is divisible by $12$ .

Is $2008$ divisible by $12$ ?
The number is divisible by $4$ and not divisible by $3$ . So, it is concluded that the number is not divisible by $12$ .

Is $720$ divisible by $12$ ?
The number is divisible by $4$ and $3$ , So, it is concluded that the number is divisible by $12$ .

Divisibility by $15$

Consider the number $3xx5xx2351$ . It is divisible by $15$ as it has $3$ and $5$ as factors.

Test for Divisibility by $15$ : If a dividend is divisible by $3$ and divisible by $5$ then it is divisible by $15$

Is $2000$ divisible by $15$ ?
The number is divisible by $5$ but not by $3$ . So it is not divisible by $15$ .

Is $990$ divisible by $15$ ?
The number is divisible by $3$ and also divisible by $5$ . So it is divisible by $15$ .

summary

Simplification by Subtraction for Divisibility Tests: To perform divisibility test on a large number, a multiple of a divisor can be subtracted and the divisibility test is performed on the difference.

Simplification by Division: Dividend can be divided by a factor, that is co-prime of divisor, and the result is checked for divisibility.

Simplification by Factors: To simplify divisibility test of dividend by a divisor,

• any common factors can be removed from both the numbers and divisibility test can be performed on simplified dividend by the simplified divisor.

• the dividend has to have all the factors of the divisor to pass the divisibility test.

Test for Divisibility by $8$ : If the last three digits of the dividend is divisible by $8$ , then the dividend is divisible by $8$ .

Test for Divisibility by $12$ : If a number is divisible by $3$ and $4$ , then the number is divisible by $12$ .

Test for Divisibility by $15$ : If a dividend is divisible by $3$ and divisible by $5$ then it is divisible by $15$

Outline

The outline of material to learn "Divisibility in Whole Numbers" is as follows.

Note: click here for detailed outline of Whole divisors

→ Classification as odd, even, prime, and composite

→ Factors, Multiples, Prime factorization

→ Highest Common Factor

→ Lowest Common Multiple

→ Introduction to divisibility tests

→ Simple Divisibility Tests

→ Simplification of Divisibility Tests

→ Simplification in Digits for Divisibility Tests