Divisibility in Whole Numbers : Common Multiples & LCM

maths > wholedivisors

Common Multiples & LCM

what you'll learn...

overview

This page provides a brief overview of

common multiples of two or more numbers,

lowest common multiple of two or more numbers,

least common multiple using factorization method,

product of numbers equals product of their LCM and HCF

Common Multiples

The multiples of $6$ $6$ are $12, 18, 24, 30, 36, 42, 48, ...$ $12,18,24,30,36,42,48, ...$ and the multiples of $8$ $8$ are $16, 24, 32, 40, 48, ...$ $16,24,32,40,48, ...$ .

What are the common multiples in these two are " $24, 48, 72, ...$ $24,48,72,...$ "

Common Multiples : Multiples common between two or more numbers are common multiples of those numbers.

The common multiples of $2$ $2$ and $4$ are " $4,8,12, cdots$ ".

The common multiples of $8$ and $3$ are " $24,48, cdots$ "

Least Common Multiple

The multiples of $6$ are $12,18,24,30,36,42,48, ...$ and the multiples of $8$ are $16,24,32,40,48, ...$ .

The common multiples are $24, 48, 72, ...$

The least value in the common multiples is " $24$ "

Least Common Multiple : The lowest multiple in the common multiples of two or more numbers is the least common multiple (LCM) of those numbers.

Find the LCM of $2$ and $4$ is " $4$ ".

The multiples of $2$ are $2, 4, 6, 8, cdots$ .

The multiples of $4$ are $4, 8, 12, cdots$ .

The common multiples are $4,8,12,cdots$ .

The least of the common multiples is $4$ .

The LCM of $15$ and $10$ is " $30$ ".

The multiples of $15$ are $15, 30, 45, 60, cdots$ .

The multiples of $10$ are $10, 20, 30, cdots$ .

The common multiples are $30,60,cdots$ .

The least of the common multiples is $30$ .

LCM Factorization Method

Consider finding the LCM of $36$ and $48$ . It is not simple to list the multiples of the large

"Prime factorization of numbers" helps to simplify the problem of finding LCM of large numbers.

Consider finding the LCM of $36$ and $48$ .

A simplified procedure is given in the figure. The numbers are divided successively by common factors. The common factors and non-common factors are multiplied to get LCM.

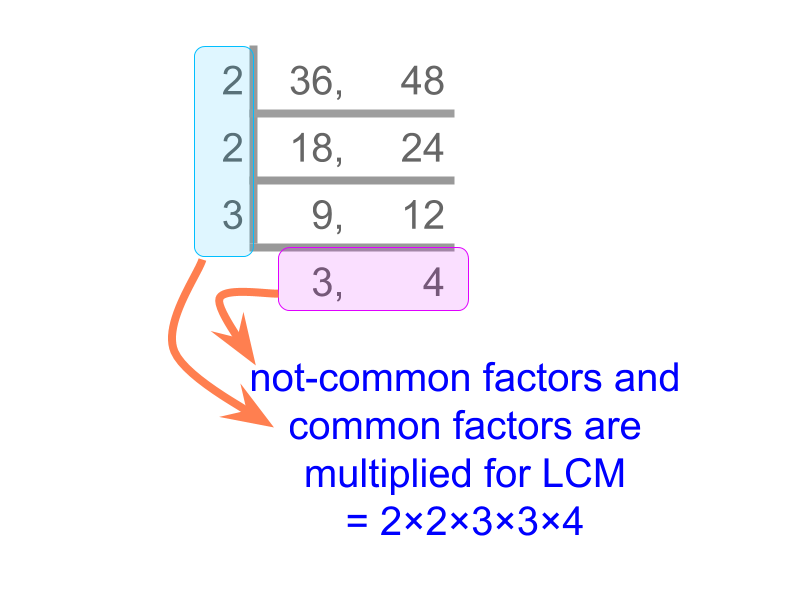
simplified procedure to find least common multiple

Factorization Method to find LCM : The numbers are successively divided by common factors. Product of common factors and the non-common factors is the LCM.

Find the LCM of $280$ and $420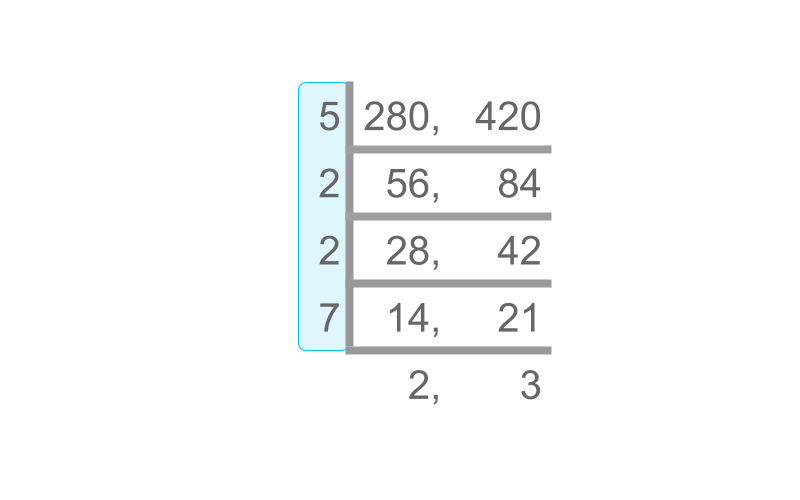$ . lcm using factorization method The Factorization Method is used to find the LCM. The answer is " $840$ ".

Relation between two numbers, their LCM and HCF

The HCF of $36$ and $48$ is " $12$ ". hcf

The LCM of $36$ and $48$ is " $144$ ". lcm using factorization method

Consider the example : finding HCF of two numbers. From this, it is understood that HCF is "product of common prime-factors".

Consider the example : finding LCM of two numbers. From this, it is understood that LCM is "product of common and non-common prime-factors".

Consider two numbers with HCF $n$ . The numbers can be given in the form $nxxp$ and $nxxq$ .

For example, HCF $36$ and $48$ is $12$ .
And $36=12xx3$ and $48=12xx4$ .
In this example $n=12$ , $p=3$ and $q=4$ .

The $p$ and $q$ are derived from the non-common prime factors of the two numbers. What is the $LCM$ of the two numbers $nxxp$ and $nxxq$ ?
The answer is " $nxxpxxq$ "

Given two numbers $nxxp$ and $nxxq$ where $n$ is the HCF and $nxxpxxq$ is the LCM.

Is there a relation between the two numbers, the HCF and the LCM?
The answer is "both the following".
product of the numbers equal product of LCM and HCF and
$(nxxp)xx(nxxq) = text( HCF ) xx text( LCM )$

LCM HCF Product Property : Product of LCM and HCF equals product of the numbers.

Given LCM $440$ and HCF $22$ . One number is $88$ what is the other number?
The answer is " $110$ ".

As per the LCM HCF Product Property
$440 xx 22 = 88 xx text( number )$

number = $440xx22 -:88$
$=110$

summary

Common Multiples : Multiples common between two or more numbers are common multiples of those numbers.

Least Common Multiple : The lowest multiple in the common multiples of two or more numbers is the least common multiple (LCM) of those numbers.

Factorization Method to find LCM : The numbers are successively divided by common factors. Product of common factors and the non-common factors is the LCM. simplified procedure to find least common multiple

LCM HCF Product Property : Product of LCM and HCF equals product of the numbers.

Outline

The outline of material to learn "Divisibility in Whole Numbers" is as follows.

Note: click here for detailed outline of Whole divisors

→ Classification as odd, even, prime, and composite

→ Factors, Multiples, Prime factorization

→ Highest Common Factor

→ Lowest Common Multiple

→ Introduction to divisibility tests

→ Simple Divisibility Tests

→ Simplification of Divisibility Tests

→ Simplification in Digits for Divisibility Tests