Exponents : Representation of Squares and Square Roots

maths > exponents

Representation of Squares and Square Roots

what you'll learn...

overview

In this page, square of a number and square root of a number are revised. The long division method to find the square root is explained.

square

We studied in exponents that $3^{2} = 3 \times 3 = 9$ $3^2 = 3 xx 3 = 9$ .

An exponent of power $2$ $2$ is called square of the number.

eg: Square of $7$ $7$ is $7^{2} = 49$ $7^2 = 49$ .

The word "square" means : the 2D shape of equal sides and $90^{\circ}$ $90^@$ angles" between the sides. The exponent square is representative of "area of the shape square, side to the power $2$ $2$ ".

root

We studied in the exponents that $16^{\frac{1}{2}} = \sqrt[2]{16} = 4$ $16^(1/2) = root(2)(16) = 4$ ".

An exponent of power $\frac{1}{2}$ $1/2$ or the $2$ $2$ nd root is called square root of the number.

eg: Square root of $64$ $64$ is $64^{\frac{1}{2}} = \sqrt[2]{64} = 8$ $64^(1/2) = root(2)(64) = 8$ .

The power of the root need not be mentioned for square roots
$\sqrt[2]{64} = \sqrt{64}$ $root(2)(64) = sqrt(64)$ .

examples

Square of $4$ $4$ is $4^{2}$ $4^2$ .

Square root of $9$ $9$ is $\sqrt[2]{9} = 9^{\frac{1}{2}}$ $root(2)(9) = 9^(1/2)$ .

$\sqrt{100} = 100^{\frac{1}{2}} = 10$ $sqrt(100) = 100^(1/2) = 10$ ".

the symbol $\sqrt{}$ $sqrt()$ is the square root.

definitions

Square of a number : A number multiplied by itself is the square of the number.
eg: $6^{2} = 6 \times 6 = 36$ $6^2 = 6xx6 = 36$

Square Root of a number : Square root of a value is the number whose square is the given value.
eg: $\sqrt{36} = 6$ $sqrt(36) = 6$ as $6^{2} = 36$ $6^2=36$ .

factorize

The factors of $26$ $26$ are " $1, 2, 13, 26$ $1, 2, 13, 26$ "

The factors of $28$ $28$ are " $1, 2, 4, 7, 14, 28$ $1,2,4,7,14,28$ "

The prime factorization of $264$ $264$ is $2 \times 2 \times 2 \times 3 \times 11$ $2xx2xx2xx3xx11$ .
A procedure is illustrated in the figure.

finding square roots

Consider finding the result of $\sqrt{3600}$ $sqrt(3600)$ .

Square root is a form of root. In roots, we learned to perform prime factorization to find the root.
$\sqrt{3600}$ $sqrt(3600)$
$= \sqrt{2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 5 \times 5}$ $=sqrt(2xx2xx2xx2xx3xx3xx5xx5)$
$= 2 \times 2 \times 3 \times 5$ $=2xx2xx3xx5$
$= 60$ $=60$

Finding Square Roots : To find square root of a number, express the number in prime factors and group the factors.

eg: $\sqrt{100}$ $sqrt(100)$ $= \sqrt{2 \times 2 \times 5 \times 5}$ $=sqrt(2xx2xx5xx5)$ $= 2 \times 5 = 10$ $=2xx5 =10$

Note: This method is suitable for finding square roots resulting in integers.

example

What is the $\sqrt{8}$ $sqrt(8)$
The answer is " $2 \sqrt{2}$ $2 sqrt(2)$ ".

Using the prime factorization method
$\sqrt{8}$ $sqrt(8)$
$= \sqrt{2 \times 2 \times 2}$ $=sqrt(2xx2xx2)$
$= 2 \times \sqrt{2}$ $=2xxsqrt(2)$

The prime factorization method is suitable for square roots resulting in integer values.

a procedure

Square root of a number can be given as
$x^{2} = {(10 a + b)}^{2}$ $x^2=(10a+b)^2$
$x^{2} = 100 a^{2} + (20 a b) + b^{2}$ $x^2=100a^2+(20ab)+b^2$

Note:
$b^{2}$ $b^2$ is a $2$ $2$ digit number with tens-units places
$100 a^{2}$ $100a^2$ is a number that has $00$ $00$ at tens-units places

This understanding gives a method to eliminate $b$ $b$ and look at $a$ $a$ to choose the highest digit of the square root.

$x^{2} = 100 a^{2} + (20 a + b) \times b$ $x^2=color(coral)(100a^2)+color(deepskyblue)((20a+b) xx b)$
$x^{2} - 100 a^{2} = (20 a + b) \times b$ $x^2 color(coral)(- 100a^2)= color(deepskyblue)((20a+b) xx b)$

The rearranged one with $(20 a + b)$ $(20a+b)$ gives the method to multiply $a$ $a$ by $2$ $2$ (which is $2 a$ $2a$ ) and append a value $b$ $b$ , which is $20 a + b$ $20a+b$ . Then multiply $b$ $b$ to $20 a + b$ $20a+b$ .

step 1
$x^{2} - a^{2} at 100s place = y$ $x^2 color(coral)(- a^2 text( at 100s place)) = y$
step 2
$y - (2 a joined with b) \times b$ $y - color(deepskyblue)((2a text( joined with ) b) xx b)$

In this process, the choice of $a$ $a$ and $b$ $b$ make the square root $x = 10 a + b = a joined with b$ $x=10a+b = a text( joined with )b$

The above process is explained for 2 digit square root and is easily extended for higher number of digits.

example using the procedure

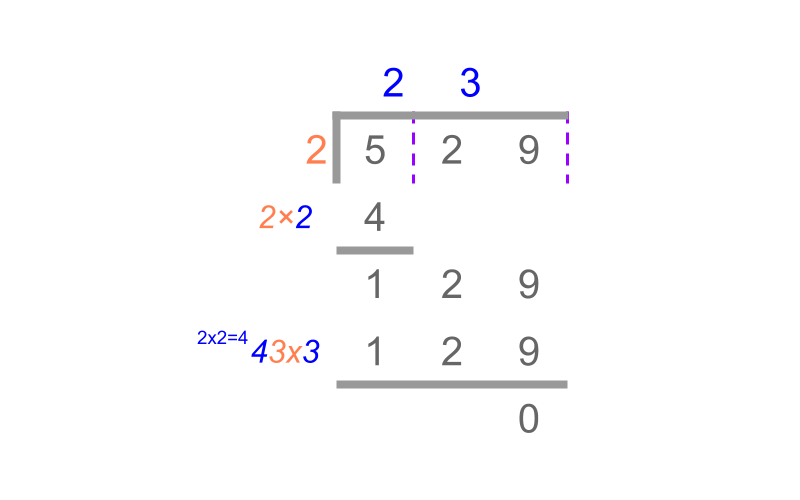
Consider $\sqrt{529}$ $sqrt(529)$

$529$ $529$
$= 23^{2}$ $=23^2$
$= {(10 \times 2 + 3)}^{2}$ $=(10xx2+3)^2$
$= {(10 \times 2)}^{2} + 2 \times 10 \times 2 \times 3 + 3^{2}$ $=(10xx2)^2+ 2 xx 10xx2 xx 3+3^2$
$= 100 \times 2^{2} + (2 \times 2 \times 10 + 3) \times 3$ $=color(coral)(100xx2^2)+color(deepskyblue)((2xx2xx10 + 3)xx3)$
$= 2^{2} 100s place + (2 \times 2 joined 3 = 43) \times 3$ $=color(coral)(2^2 text( 100s place ))+color(deepskyblue)((2xx2 text( joined )3 = 43)xx 3)$

The above steps is used in reverse when the square root is not known
$\sqrt{529}$ $sqrt(529)$
$= 2 at 10s place + 3 at units place$ $=color(coral)(2) text( at 10s place ) + color(deepskyblue)(3) text( at units place)$
$= 23$ $=23$

This procedure is illustrated in the figure.

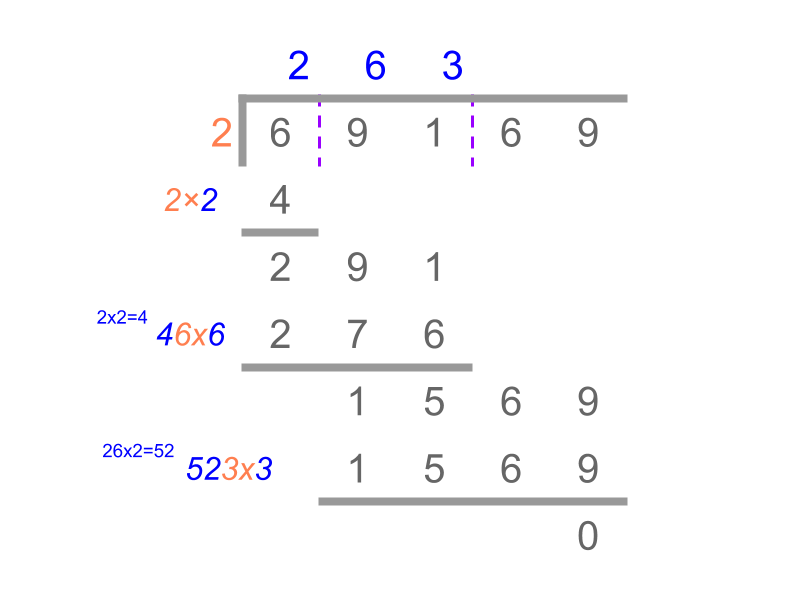
$\sqrt{69169} = 263$ $sqrt(69169) = 263$ square root long division

summary

Procedure to finding Square Root of a number : Long division method is illustrated in the figure.
square root long division

Outline

The outline of material to learn "Exponents" is as follows. Note: click here for detailed outline of Exponents s

→ Representation of Exponents

→ Inverse of exponent : root

→ Inverse of exponent : Logarithm

→ Common and Natural Logarithms

→ Exponents Arithmetics

→ Logarithm Arithmetics

→ Formulas

→ Numerical Expressions

→ PEMA / BOMA

→ Squares and Square roots

→ Cubes and Cube roots