Differential Calculus : Differentiation: Graphical Meaning

maths > differential-calculus

Differentiation: Graphical Meaning

what you'll learn...

Overview

» Graphical Meaning of Derivative: slope of the tangent

derivative reference     → at a point $x = a$ $x=a$ , the rate of change of the curve is $f' (a)$ $f′(a)$

    → at a point $x = a$ $x=a$ , the slope of the tangent is $f' (a)$ $f′(a)$ .

    → at the maxima of the curve $f (a_{1})$ $f(a_1)$ , the derivative $f' (a_{1})$ $f′(a_1)$ crosses $0$ $0$ from positive rate of change to negative rate of change.

    → at the minima of the curve $f (a_{2})$ $f(a_2)$ , the derivative $f' (a_{2})$ $f′(a_2)$ crosses $0$ $0$ from negative rate of change to positive rate of change.

recap

Summary of differentiation: Given $y = f (x)$ $y=f(x)$ a function of variable $x$ $x$ , the derivative of $y$ $y$ is

$\frac{d y}{d x}$ $(dy)/(dx)$ $= lim_{δ \to 0} \frac{f (x + δ) - f (x)}{δ}$ $= lim_(delta->0) (f(x+delta) - f(x))/delta$ .

"The derivative is another function of variable $x$ $x$ ".

For some functions, the derivatives are numerical values. That is, the derivative is not a numerical value for all functions.

graphical

Let us consider $y = \frac{x^{2}}{2}$ $y=(x^2)/2$ and $\frac{d y}{d x} = x$ $(dy)/(dx) = x$ . The figure depicts both the functions. Blue color curve is $y = \frac{x^{2}}{2}$ $y=(x^2)/2$ and orange color line is $\frac{d y}{d x} = x$ $(dy)/(dx) = x$ .
note: The plot is not to the scale on x and y axes.

The rate of change of blue curve is plotted as orange line.

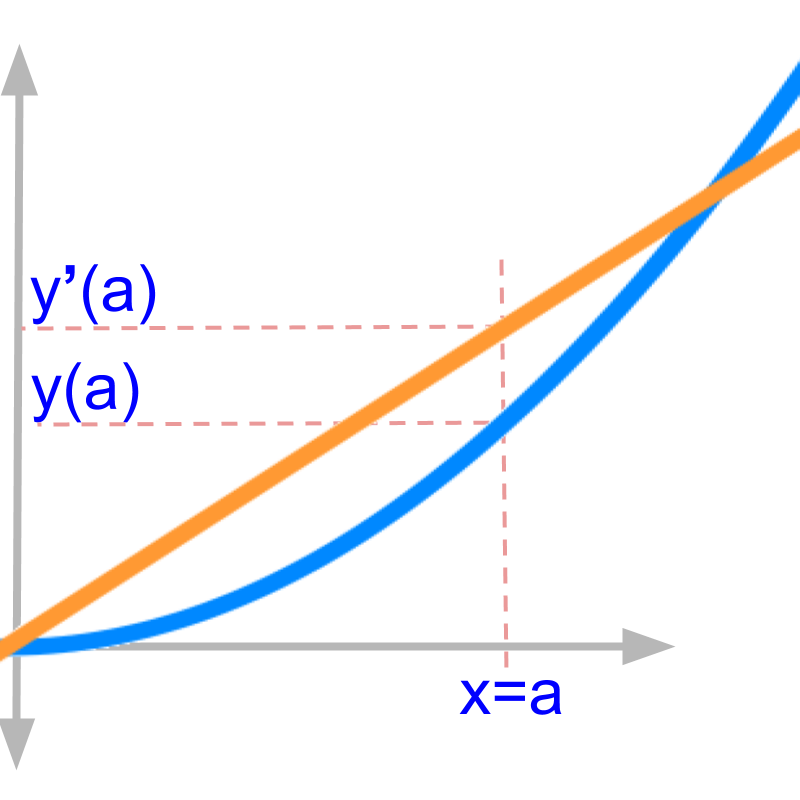
The figure zooms in a small part of the plots.

• $y (a)$ $y(a)$ is the value function evaluates to at $x = a$ $x=a$

• $y' (a)$ $y′(a)$ is the rate of change of $y$ $y$ at $x = a$ $x=a$

This result is known from the algebraic derivations. Let us see what this means in the given curve.

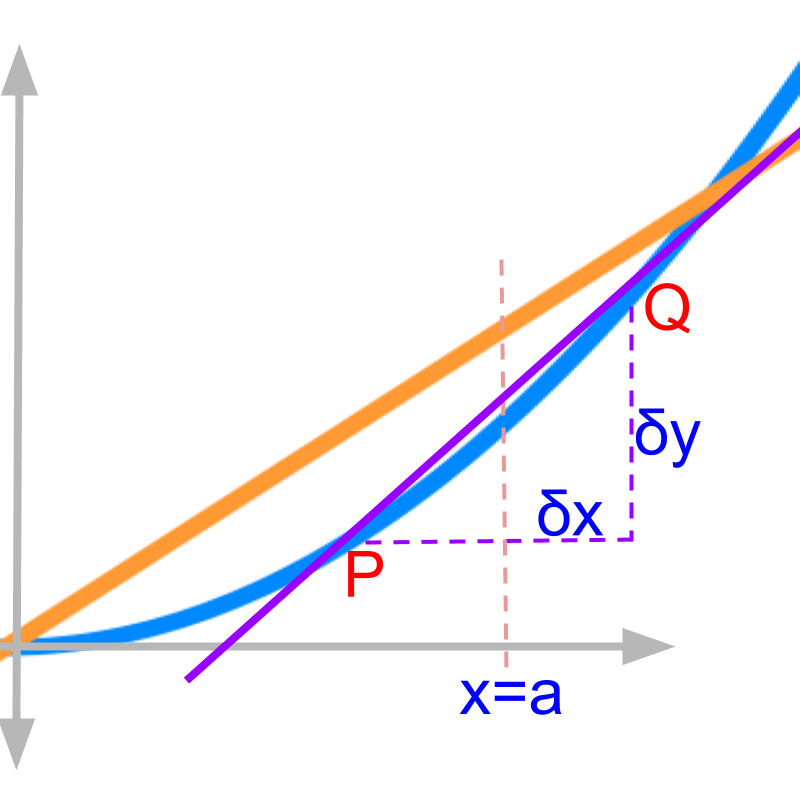
Considering $y = \frac{x^{2}}{2}$ $y=(x^2)/2$ and $\frac{d y}{d x} = x$ $(dy)/(dx) = x$ given in the figure.

The derivative in first principles is given as
$y' (x)$ $y′(x)$
$= \frac{d}{d x} y$ $= d/(dx) y$
$= lim_{δ x \to 0} \frac{δ y}{δ x}$ $= lim_(delta x->0) (delta y)/(delta x)$

$δ x$ $delta x$ at $x = a$ $x=a$ is shown in the figure.
$δ y$ $delta y$ for the $δ x$ $delta x$ is shown in the figure.

the derivative is derived using limit $δ x$ $delta x$ tending to $0$ $0$

The figure shows non-zero $δ x$ $delta x$ and corresponding $δ y$ $delta y$ before limit is applied.

The points $P$ $P$ and $Q$ $Q$ are on the curve separated by $δ x$ $delta x$ on $x = a$ $x=a$ . Consider the line passing through the points $P$ $P$ and $Q$ $Q$ . The line is a secant as the line passes through two points on the curve.

It shows non-zero $δ x$ $delta x$ and corresponding $δ y$ $delta y$ before limit is applied. The slope of the line $\bar{P Q}$ $bar(PQ)$ is " $\frac{δ y}{δ x}$ $(delta y)/(delta x)$ ". The line passing through the points $P (x_{1}, y_{1})$ $P(x_1, y_1)$ and $Q (x_{1} + δ x, y_{1} + δ y)$ $Q(x_1+delta x, y_1+delta y)$
Slope of the secant
$= \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ $=(y_2-y_1)/(x_2-x_1)$
$= \frac{δ y}{δ x}$ $=(delta y)/(delta x)$

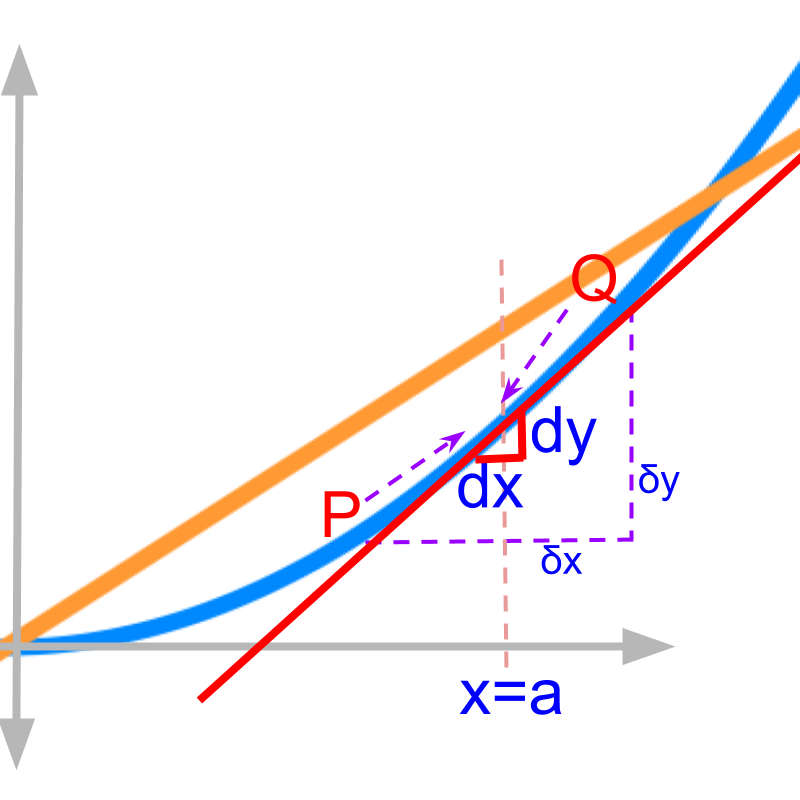
Considering $y = \frac{x^{2}}{2}$ $y=(x^2)/2$ and $\frac{d y}{d x} = x$ $(dy)/(dx) = x$ given in the figure.

The derivative in first principles is given as
$y' (x)$ $y′(x)$
$= lim_{δ x \to 0} \frac{δ y}{δ x}$ $= lim_(delta x->0) (delta y)/(delta x)$

Applying the limit, the $δ x$ $delta x$ and $δ y$ $delta y$ reduces "close to $0$ $0$ ", which is shown in red.
The points $P$ $P$ and $Q$ $Q$ at the two ends of $d x$ $dx$ moves towards each other. When limit $δ x$ $delta x$ is close to zero, the two points $P$ $P$ and $Q$ $Q$ merge to become a single point. The points $P$ $P$ and $Q$ $Q$ move towards each other and merge.

The line passing through $P$ $P$ and $Q$ $Q$ is shown in red. As the limit is applied, the line touches the curve in only one point

The line is a "tangent", as the line touches at a single point on the curve.

The slope of the tangent at $x = a$ $x=a$ is " $\frac{d y}{d x} ∣_{x = a}$ $(dy)/(dx)|_(x=a)$ ". The rate of change is the slope at that point.

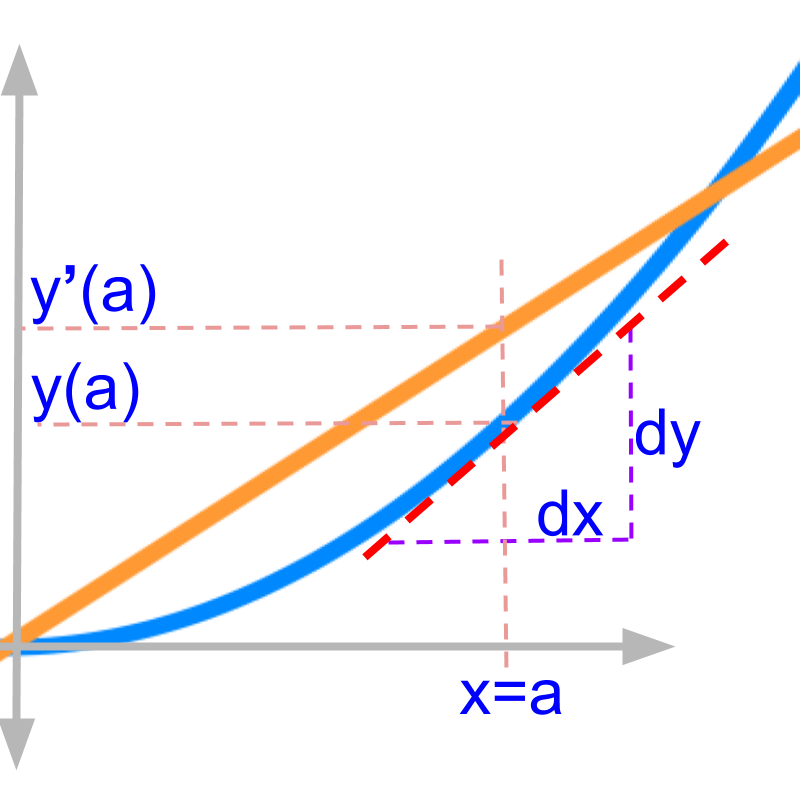
$\frac{d y}{d x} ∣_{x = a}$ $(dy)/(dx)|_(x=a)$ is the slope of the tangent on curve $y$ $y$ at position $x = a$ $x=a$ . The tangent is shown in red dotted line.

analysing the curves

For a function $f (x)$ $f(x)$ , the slope of tangent at $x = a$ $x=a$ is $\frac{d}{d x} f (x) ∣_{x = a}$ $d/(dx) f(x)|_(x=a)$ .The figure shows $f (x)$ $f(x)$ in blue and $\frac{d}{d x} f (x)$ $d/(dx) f(x)$ in orange. Three positions are identified with $3$ $3$ vertical lines.

The slope of $f (x)$ $f(x)$ at the position $P$ $P$ is negative or decreasing rate of change. This is also evident from the negative value at the same position in orange line.

The slope of $f (x)$ $f(x)$ at the position $Q$ $Q$ is "positive or increasing rate of change". This is also evident from the positive value at the same position in orange line.

The slope of $f (x)$ $f(x)$ at the position $x = 0$ $x=0$ is "zero". This is also evident from the zero value at the same position in orange line.

Figure shows $y = x + 1$ $y=x+1$ in blue and $\frac{d y}{d x} = 1$ $(dy)/(dx) = 1$ in orange. From the figure, we understand that "the function has constant rate of change". This is evident from the flat orange line.

The figure shows $y = \sin x$ $y=sin x$ in blue and $\frac{d y}{d x} = \cos x$ $(dy)/(dx) =cos x$ in orange.

• when $y$ $y$ reaches maximum, the rate of change is $0$ $0$

• when $y$ $y$ reaches minimum, the rate of change is $0$ $0$ This is evident from the values on orange line, the derivative of the function, having value 0 at the positions of maxima and minima.

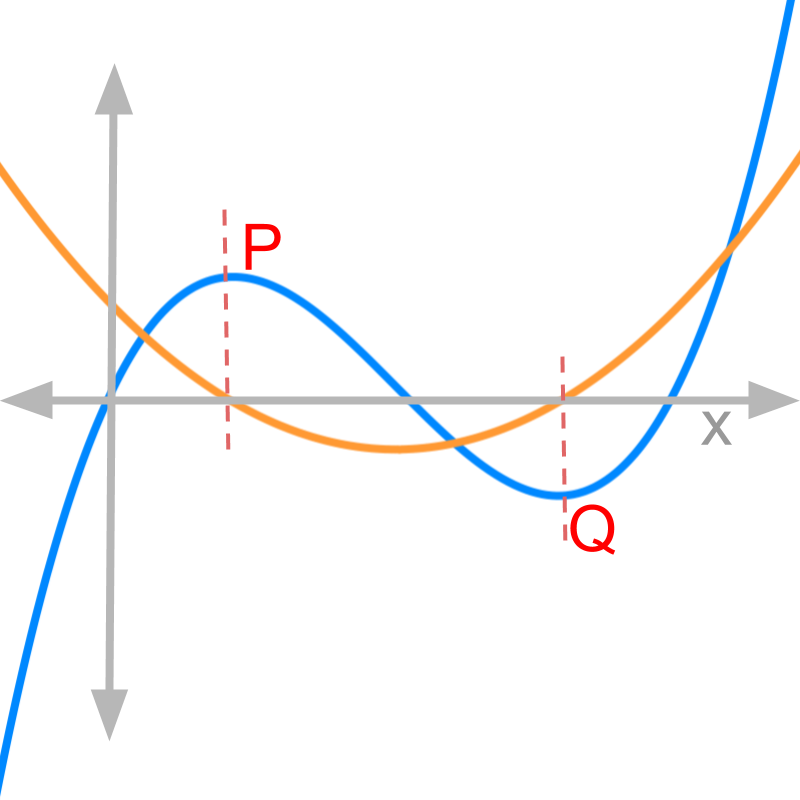
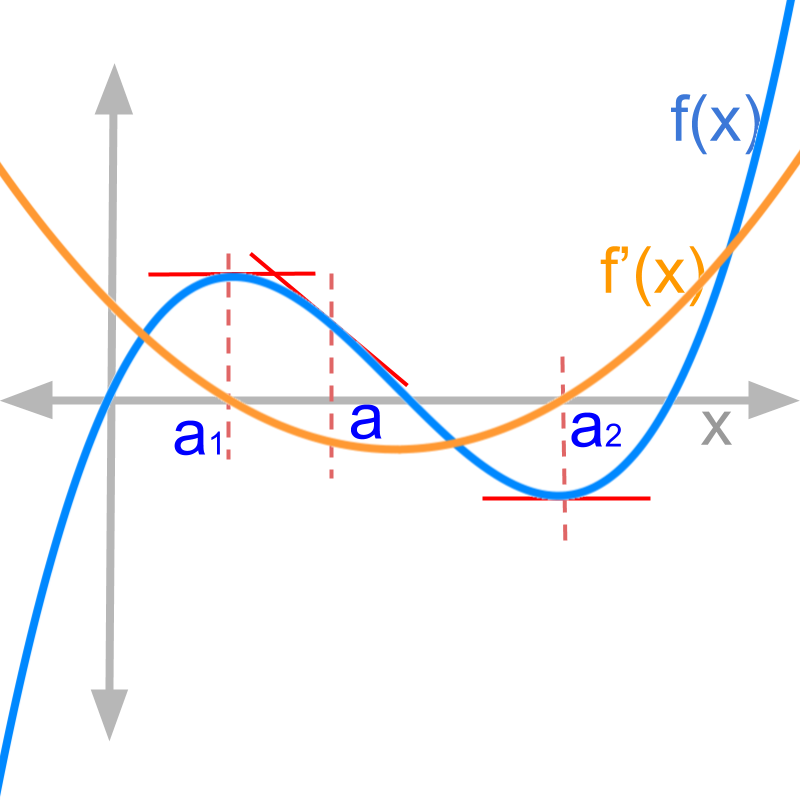
The figure shows $y$ $y$ in blue and $\frac{d y}{d x}$ $(dy)/(dx)$ in orange. Two positions are identified.

• when $y$ $y$ reaches maximum, the rate of change crosses $0$ $0$ from positive to negative

• when $y$ $y$ reaches minimum, the rate of change crosses $0$ $0$ from negative to positive

This is evident from the values on orange line, the derivative of the function, crossing the x axis at the positions of maxima and minima.

The slope of the tangent on curve is the derivative evaluated at that point.

example

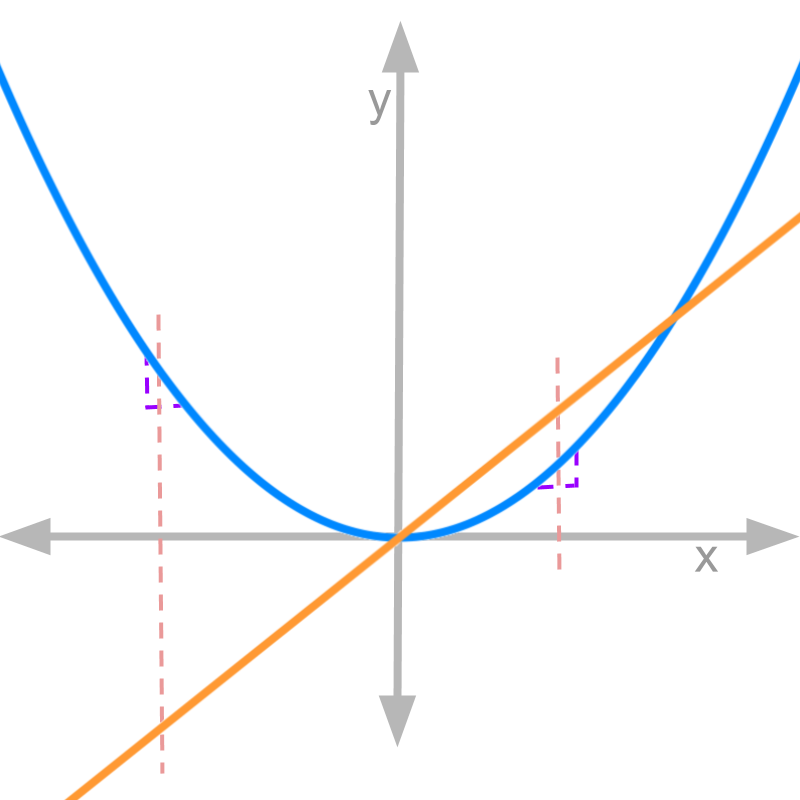
The figure shows $y$ $y$ in blue and $\frac{d y}{d x}$ $(dy)/(dx)$ in orange. The observations are

• for negative values of $x$ $x$ , the rate of change is negative

• for positive values of $x$ $x$ , the rate of change is positive

• at $x = 0$ $x=0$ , the rate of change crosses $0$ $0$ from negative to positive

summary

Graphical Meaning of Derivative: For a function $f (x)$ $f(x)$ , the derivative $f' (x)$ $f′(x)$ is another function of the variable.

• at a point $x = a$ $x=a$ , the rate of change of the curve is $f' (a)$ $f′(a)$

• at a point $x = a$ $x=a$ , the slope of the tangent is $f' (a)$ $f′(a)$ .

• at the maxima of the curve $f (a_{1})$ $f(a_1)$ , the derivative $f' (a_{1})$ $f′(a_1)$ crosses $0$ $0$ from positive rate of change to negative rate of change.

• at the minima of the curve $f (a_{2})$ $f(a_2)$ , the derivative $f' (a_{2})$ $f′(a_2)$ crosses $0$ $0$ from negative rate of change to positive rate of change.

Outline

The outline of material to learn "Differential Calculus" is as follows.

• Detailed outline of Differential Calculus

→ Application Scenario

→ Differentiation in First Principles

→ Graphical Meaning of Differentiation

→ Differntiability

→ Algebra of Derivatives

→ Standard Results