Differential Calculus : Differentiability of Functions

maths > differential-calculus

Differentiability of Functions

what you'll learn...

Overview

» A function $f (x)$ $f(x)$ is differentiable at point $x = a$ $x=a$ if the "derivative-limit" is defined at that point.

    → right-hand-limit $lim_{x \to a +} \frac{f (x) - f (a)}{x - a}$ $lim_(x->a+) (f(x)-f(a))/(x-a)$

    → left-hand-limit $lim_{x \to a -} \frac{f (x) - f (a)}{x - a}$ $lim_(x->a-) (f(x)-f(a))/(x-a)$

    → if both the limits are equal

    → and if both the limits are real numbers

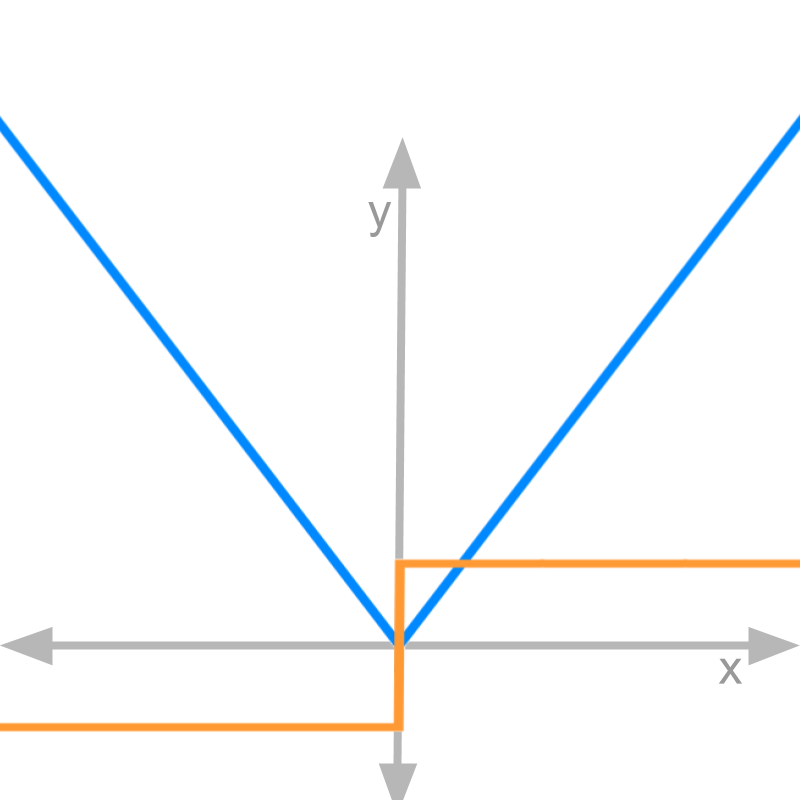derivative absolute x     → eg: $f (x) = | x |$ $f(x)=|x|$ is not differentiable at $x = 0$ $x=0$

establish the problem

Let us revise what we learned in "limits"

• when the function evaluates to indeterminate value $0 / 0$ $0//0$ , limit of the function helps to resolve its value.

• The function is defined at a point, if left-hand-limit and right-hand-limit are equal at the given point.

• The function is not defined at a point, if left-hand-limit and right-hand-limit are not equal at the given point.

• When, left-hand-limit and right-hand-limit are equal, it is commonly referred as limit of the function.

The derivative of a function $f (x)$ $f(x)$ is the instantaneous rate of change given as
$lim_{δ \to 0} \frac{f (x + δ) - f (x)}{δ}$ $lim_(delta ->0) (f(x+delta) - f(x))/(delta)$

The left-hand-limit and right-hand-limit are applicable to this expression. And fot some functions, LHL and RHL are to be computed to establish that this limit exists. The objective of this lesson is to learn when the LHL and RHL are computed.

positive side of mod x

The figure shows $y = | x |$ $y=|x|$ in blue. We need to compute $\frac{d y}{d x}$ $(dy)/(dx)$ .

$y = {\begin{cases} x & for x > 0 \\ - x & for x < 0 \\ 0 & for x = 0 \end{cases}$ $y= { (x , text( for ) x>0), (-x , text( for ) x <0), (0 , text( for ) x =0):}$

Derivative by first principles
$\frac{d y}{d x} ∣_{x = a}$ $(dy)/(dx)|_(x=a)$
for $x > 0$ $x>0$ : $| x | = x$ $|x|=x$ and $| a | = a$ $|a|=a$
right-hand-limit
$= lim_{x \to a + δ} \frac{f (x) - f (a)}{x - a}$ $= lim_(x->a+delta) (f(x)-f(a))/(x-a)$
$= lim_{x \to a + δ} \frac{| x | - | a |}{x - a}$ $= lim_(x->a+delta) (|x|-|a|)/(x-a)$

$= lim_{x \to a + δ} \frac{x - a}{x - a}$ $= lim_(x->a+delta) (x-a)/(x-a)$
$= \frac{a + δ - a}{a + δ - a}$ $= (a+delta-a)/(a+delta-a)$
$= \frac{δ}{δ}$ $= (delta)/delta$
$= 1$ $= 1$

left-hand-limit
$= lim_{x \to a - δ} \frac{f (x) - f (a)}{x - a}$ $= lim_(x->a-delta) (f(x)-f(a))/(x-a)$
$= lim_{x \to a - δ} \frac{| x | - | a |}{x - a}$ $= lim_(x->a-delta) (|x|-|a|)/(x-a)$

$= lim_{x \to a - δ} \frac{x - a}{x - a}$ $= lim_(x->a-delta) (x-a)/(x-a)$
$= \frac{a - δ - a}{a - δ - a}$ $= (a-delta-a)/(a-delta-a)$
$= \frac{- δ}{- δ}$ $= (-delta)/(-delta)$
$= 1$ $= 1$

The above implies that

• the limit exists for $x > 0$ $x>0$

• the expression under limit is continuous for $x > 0$ $x>0$

Note that, the expression under limit is $\frac{f (x + δ) - f (x)}{δ}$ $(f(x+delta) -f(x))/delta$ . This expression is continuous and defined for $x > 0$ $x>0$ .

Since the expression is the derivative of the function $f (x)$ $f(x)$ , the derivative of the function is defined for $x > 0$ $x>0$ .

negative side of mod x

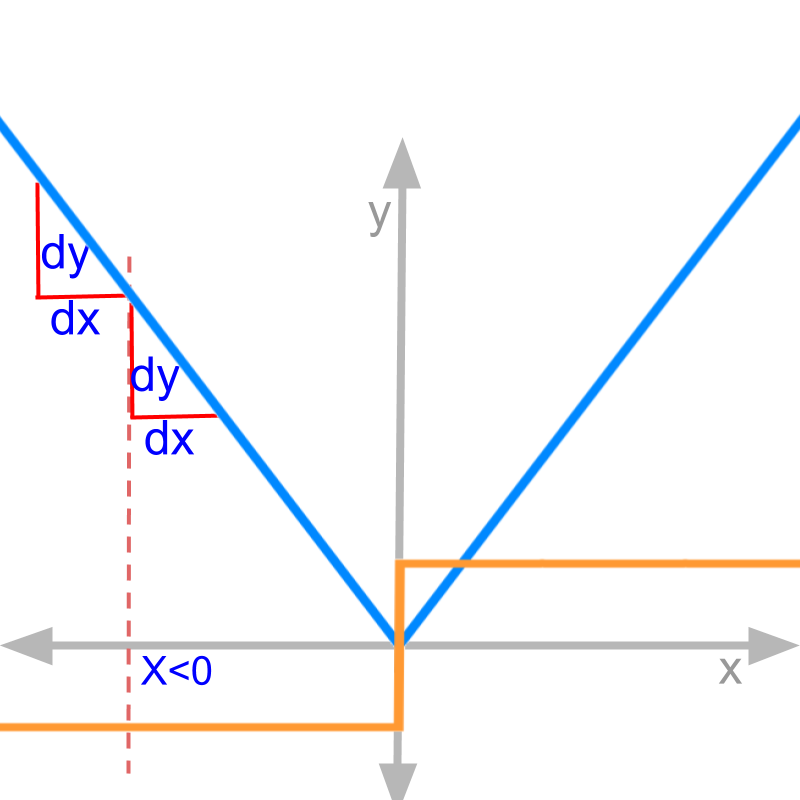
Derivative by first principles:
$\frac{d y}{d x} ∣_{x = a}$ $(dy)/(dx)|_(x=a)$
for $x < 0$ $x<0$ : $| x | = - x$ $|x|=-x$ and $| a | = - a$ $|a|=-a$
right-hand-limit
$= lim_{x \to a + δ} \frac{f (x) - f (a)}{x - a}$ $= lim_(x->a+delta) (f(x)-f(a))/(x-a)$
$= lim_{x \to a + δ} \frac{| x | - | a |}{x - a}$ $= lim_(x->a+delta) (|x|-|a|)/(x-a)$

$= lim_{x \to a + δ} \frac{- x - (- a)}{x - a}$ $= lim_(x->a+delta) (-x-(-a))/(x-a)$
$= \frac{- a - δ + a}{a + δ - a}$ $= (-a-delta+a)/(a+delta-a)$
$= \frac{- δ}{δ}$ $= (-delta)/delta$
$= - 1$ $= -1$

left-hand-limit
$= lim_{x \to a - δ} \frac{f (x) - f (a)}{x - a}$ $= lim_(x->a-delta) (f(x)-f(a))/(x-a)$
$= lim_{x \to a - δ} \frac{| x | - | a |}{x - a}$ $= lim_(x->a-delta) (|x|-|a|)/(x-a)$

$= lim_{x \to a - δ} \frac{- x - (- a)}{x - a}$ $= lim_(x->a-delta) (-x-(-a))/(x-a)$
$= \frac{- a + δ + a}{a - δ - a}$ $= (-a+delta+a)/(a-delta-a)$
$= \frac{δ}{- δ}$ $= (delta)/(-delta)$
$= - 1$ $= -1$

This implies that

• the limit exists for $x < 0$ $x<0$

• the expression under limit is continuous for $x < 0$ $x<0$

Note that, the expression under limit is $\frac{f (x + δ) - f (x)}{δ}$ $(f(x+delta) -f(x))/delta$ . This expression is continuous and defined for $x < 0$ $x<0$ .

Since the expression is the derivative of the function $f (x)$ $f(x)$ , the derivative of the function is defined for $x < 0$ $x<0$ .

mod x at 0

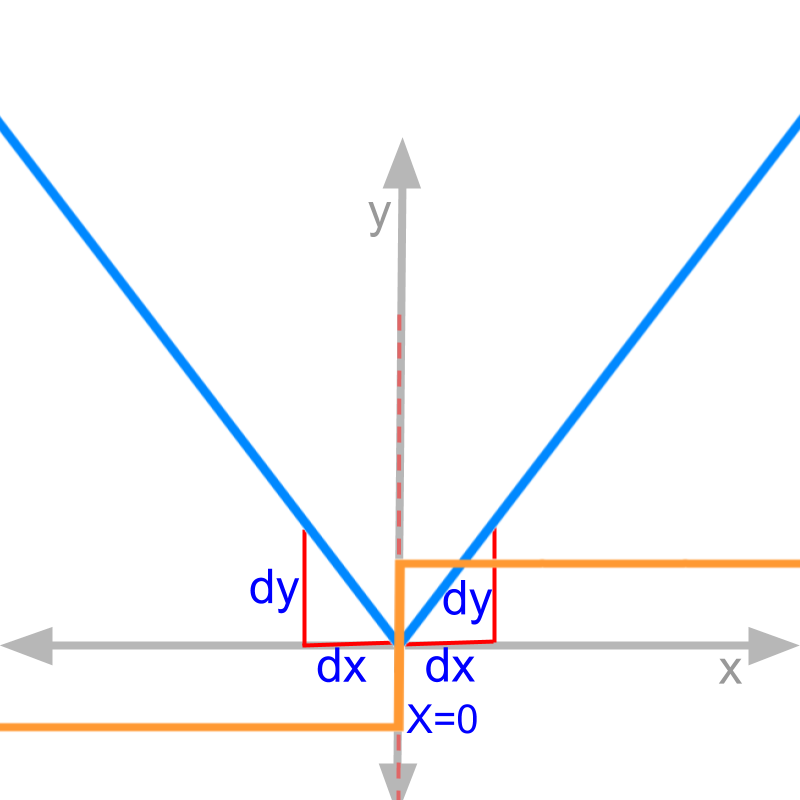
The figure shows $y = | x |$ $y=|x|$ in blue. We need to compute $\frac{d y}{d x}$ $(dy)/(dx)$ at $x = 0$ $x=0$ .

Derivative by first principles: finding limits at $x = 0$ $x=0$
$y = | \begin{matrix} x & for x > 0 \\ - x & for x < 0 \\ 0 & for x = 0 \end{matrix} |$ $y= | [x , text( for ) x>0], [-x , text ( for ) x <0], [0 , text ( for ) x =0]|$

$\frac{d y}{d x} ∣_{x = 0}$ $(dy)/(dx)|_(x=0)$

left hand limit
$= lim_{x \to 0 - δ} \frac{f (x) - f (0)}{x - 0}$ $= lim_(x->0-delta) (f(x)-f(0))/(x-0)$
$= lim_{x \to 0 - δ} \frac{| x | - | 0 |}{x - 0}$ $= lim_(x->0-delta) (|x|-|0|)/(x-0)$

for $x = 0 - δ$ $x=0-delta$ : $| x | = δ$ $|x|=delta$
$= \frac{δ - 0}{0 - δ - 0}$ $= (delta-0)/(0-delta-0)$
$= \frac{δ}{- δ}$ $= (delta)/(-delta)$
$= - 1$ $= -1$

right hand limit
$= lim_{x \to 0 + δ} \frac{f (x) - f (0)}{x - 0}$ $= lim_(x->0+delta) (f(x)-f(0))/(x-0)$
$= lim_{x \to 0 + δ} \frac{| x | - | 0 |}{x - 0}$ $= lim_(x->0+delta) (|x|-|0|)/(x-0)$

for $x = 0 + δ$ $x=0+delta$ : $| x | = δ$ $|x|=delta$
$= \frac{δ - 0}{0 + δ - 0}$ $= (delta-0)/(0+delta-0)$
$= \frac{δ}{δ}$ $= (delta)/(delta)$
$= 1$ $= 1$

At $x = 0$ $x=0$ , left-hand-limit is $- 1$ $-1$ and right-hand-limit is $1$ $1$ .

This implies that

• the limit does not exist at $x = 0$ $x=0$

• the expression under limit is not continuous at $x = 0$ $x=0$

Note that, the expression under limit is $\frac{f (x + δ) - f (x)}{δ}$ $(f(x+delta) -f(x))/delta$ . This expression is not defined at $x = 0$ $x=0$ . Since the expression is the derivative of the function $f (x)$ $f(x)$ , the derivative of the function is not defined for $x = 0$ $x=0$ .

-able suffix is can-do

The figure shows $y = | x |$ $y=|x|$ in blue.

It is proven that

• for $x < 0$ $x<0$ , the derivative is defined.

• for $x > 0$ $x>0$ , the derivative is defined.

• for $x = 0$ $x=0$ , the derivative is not defined.

This is referred as differentiability of the function.

• The function is not differentiable at $x = 0$ $x=0$ .

• The function is differentiable for $x \neq 0$ $x!=0$ .

differentiable

A function is differentiable at a point, if the instantaneous rate of change at that point is continuous.

A function is continuously differentiable, if the instantaneous rate of change is continuous for any and all points from $- \infty \to + \infty$ $-oo to +oo$

A function is continuously differentiable in a range `a
The instantaneous rate of change or the derivative-limit is given as
$lim_{δ \to 0} \frac{f (x + δ) - f (x)}{δ}$ $lim_(delta->0) (f(x+delta) - f(x))/delta$ .

tan x

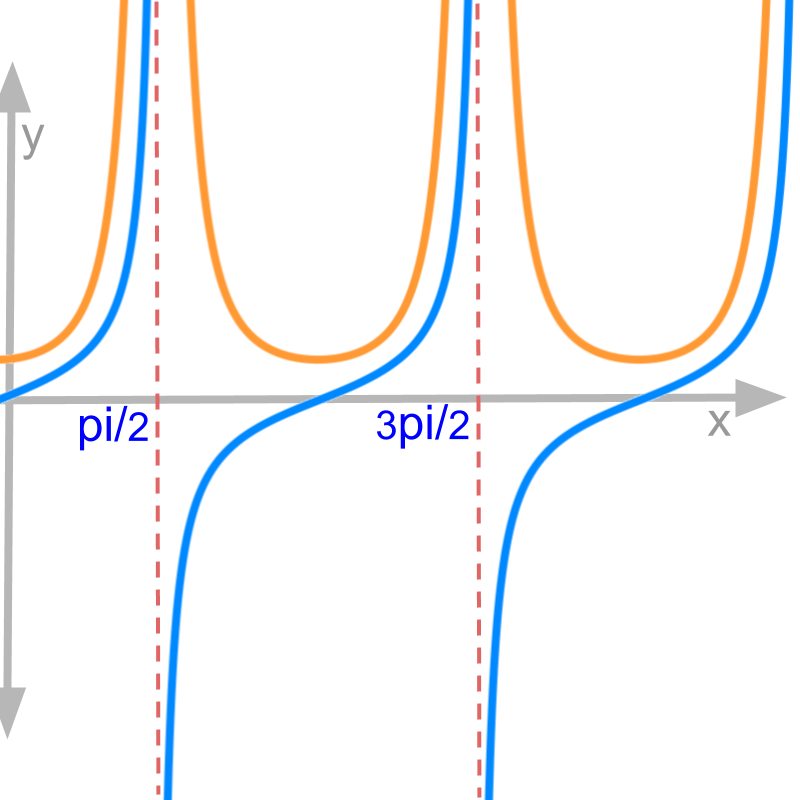
Finding differentiability of $f (x) = \tan x$ $f(x) = tan x$ .
Derivative is $\frac{d}{d x} \tan x = \sec^{2} x$ $(d)/(dx) tan x = sec^2 x$ .
the result of derivative is proven later Figure shows $\tan x$ $tan x$ in blue and $\sec^{2} x$ $sec^2 x$ in orange. From the left and right side limits of $\tan x$ $tan x$ , it is found that the function is not continuous at $x = \frac{π}{2} + n π$ $x=pi/2 + n pi$ .

At $x = \frac{π}{2} + n π$ $x=pi/2 + n pi$ where $n = 0, 1, 2, \dots$ $n=0,1,2, cdots$ ,
the derivative
$= \sec^{2} (\frac{π}{2})$ $= sec^2 (pi/2)$
$= \infty$ $= oo$
This implies that the function $\tan x$ $tan x$ is not differentiable at $x = \frac{π}{2} + n π$ $x=pi/2 + n pi$ .
It can be observed in the figure that the derivative $\sec^{2} x$ $sec^2 x$ takes very high value.

cube root x

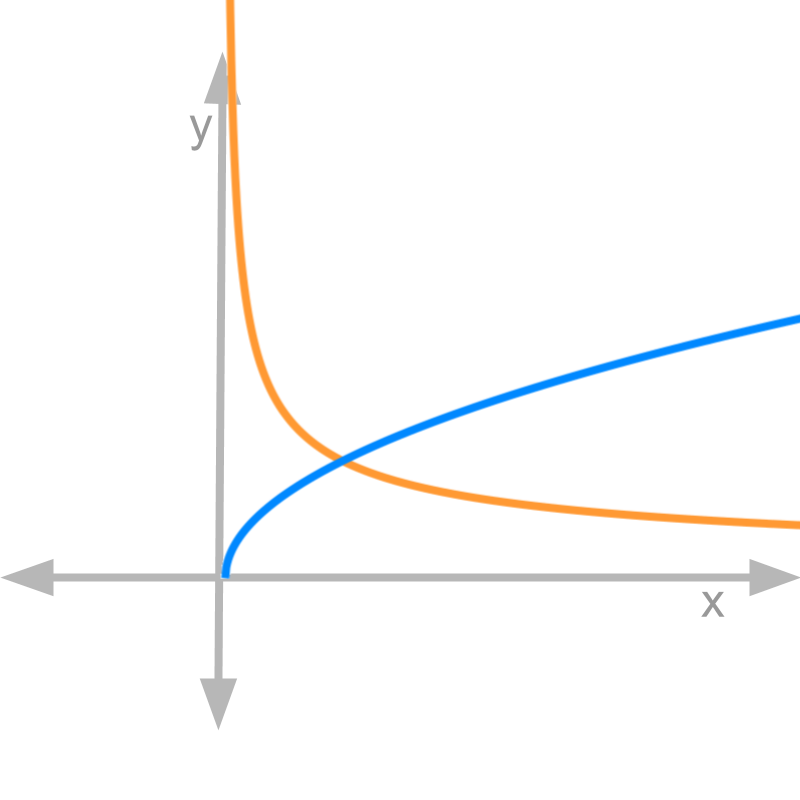
Finding differentiability of $f (x) = x^{\frac{1}{3}}$ $f(x) = x^(1/3)$ .
Derivative is $\frac{d}{d x} f (x) = x^{- \frac{2}{3}}$ $(d)/(dx) f(x) = x^(-2/3)$ .
the result of derivative is proven later Figure shows $x^{\frac{1}{3}}$ $x^(1/3)$ in blue and $x^{- \frac{2}{3}}$ $x^(-2/3)$ in orange. From the left and right side limits of $x^{\frac{1}{3}}$ $x^(1/3)$ , the function is continuous at $x = 0$ $x=0$ .
At $x = 0$ $x=0$ , the derivative
$= 0^{- \frac{2}{3}}$ $= 0^(-2/3)$
$= \infty$ $= oo$
This implies that the function is not differentiable at $x = 0$ $x=0$ .
It can be observed in the figure that the derivative $x^{- 2 / 3}$ $x^(-2//3)$ takes very high value at $x = 0$ $x=0$ .

square root

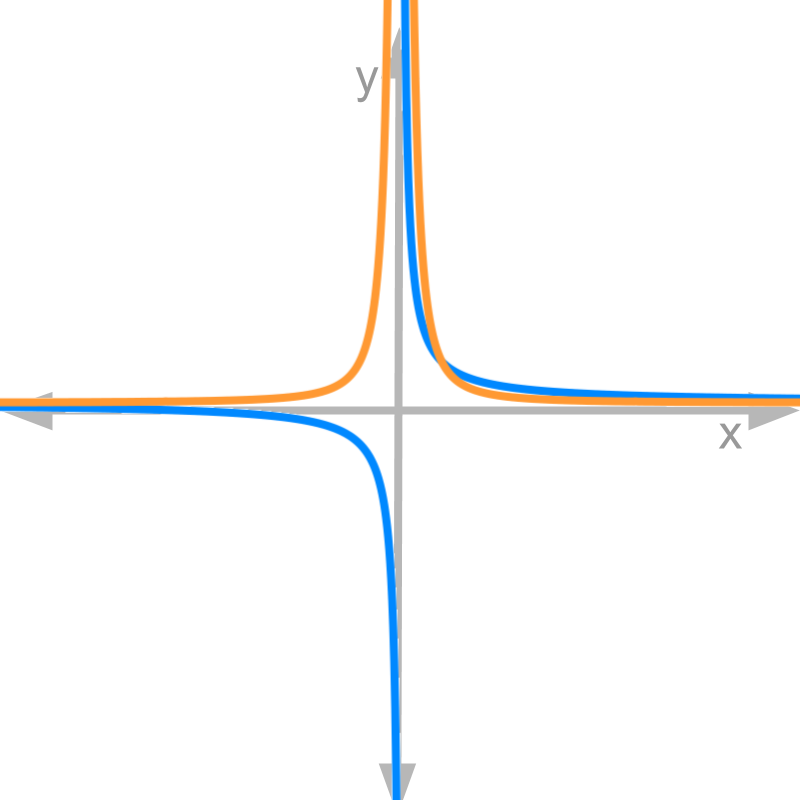
Finding differentiability of $f (x) = x^{\frac{1}{2}}$ $f(x) = x^(1/2)$ .
Derivative is $\frac{d}{d x} f (x) = x^{- \frac{1}{2}}$ $(d)/(dx) f(x) = x^(-1/2)$ .
the result of derivative is proven later Figure shows $x^{\frac{1}{2}}$ $x^(1/2)$ in blue and $x^{- \frac{1}{2}}$ $x^(-1/2)$ in orange. Note that the function is not defined for $x < 0$ $x<0$ .
This implies, the function is not differentiable for $x < 0$ $x<0$ .

reciprocal x

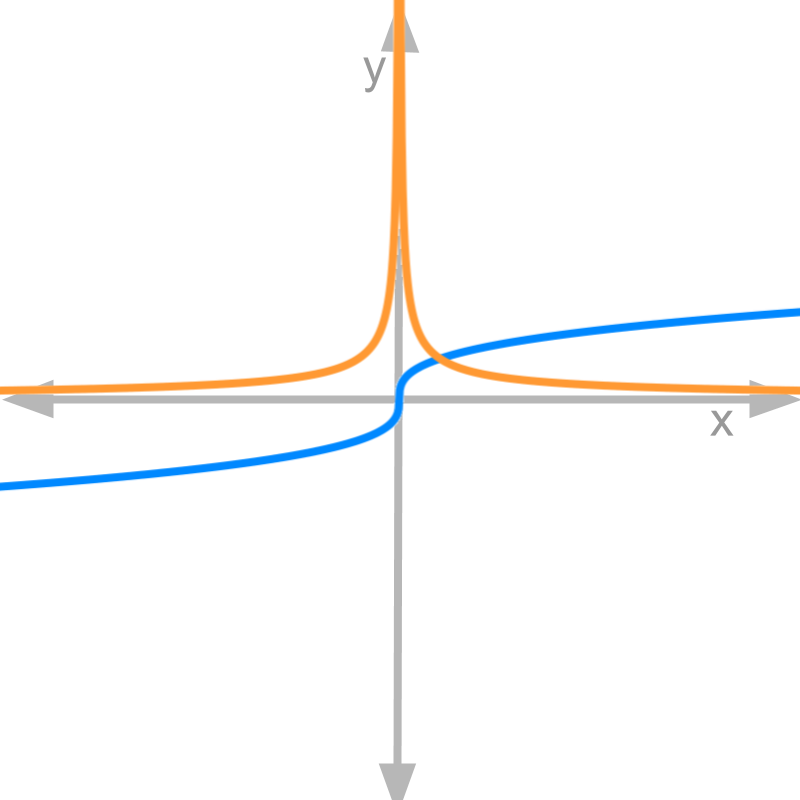
Finding differentiability of $f (x) = x^{- 1}$ $f(x) = x^(-1)$
Derivative is $\frac{d}{d x} f (x) = x^{- 2}$ $(d)/(dx) f(x) = x^(-2)$ .
the result of derivative is proven later

Figure shows $x^{- 1}$ $x^(-1)$ in blue and $x^{- 2}$ $x^(-2)$ in orange. From the left and right side limits of $x^{- 1}$ $x^(-1)$ , it is derived that the function is not continuous at $x = 0$ $x=0$ .
At $x = 0$ $x=0$ , the derivative
$= 0^{- 2}$ $= 0^(-2)$
$= \infty$ $= oo$
Is $x^{- 1}$ $x^(-1)$ a continuously differentiable function?

The answer is "No. It is not differentiable at $x = 0$ $x=0$ ". It can be observed in the figure that the derivative $x^{- 2}$ $x^(-2)$ takes very high value at $x = 0$ $x=0$ .

reciprocal x squared

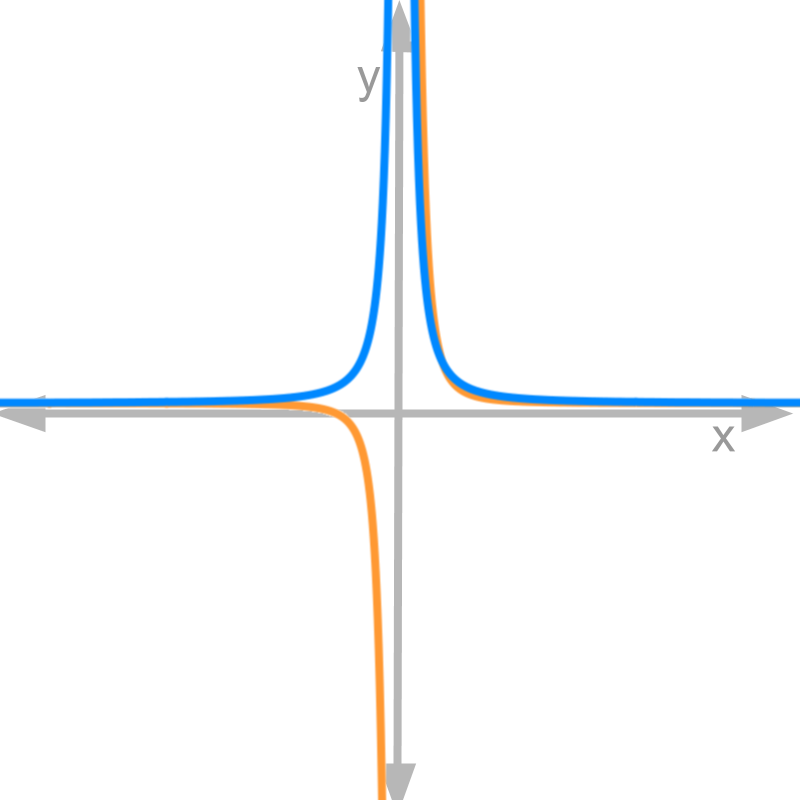
Finding differentiability of $f (x) = x^{- 2}$ $f(x) = x^(-2)$ .
Derivative is $\frac{d}{d x} f (x) = x^{- 3}$ $(d)/(dx) f(x) = x^(-3)$ .
the result of derivative is proven later

Figure shows $x^{- 2}$ $x^(-2)$ in blue and $x^{- 3}$ $x^(-3)$ in orange. From the left and right side limits of $x^{- 2}$ $x^(-2)$ , it is derived that the function is not continuous at $x = 0$ $x=0$ .
At $x = 0$ $x=0$ , the derivative
$= \frac{d}{d x} x^{- 2} ∣_{x = 0}$ $= d/(dx) x^(-2)|_(x=0)$
from right and left hand limits
$= \pm \infty$ $= +-oo$
Is $x^{- 2}$ $x^(-2)$ a continuously differentiable function?

The answer is "No. It is not differentiable at $x = 0$ $x=0$ ". It can be observed in the figure that the derivative $x^{- 3}$ $x^(-3)$ takes $\pm \infty$ $+-oo$ at $x = 0$ $x=0$ .

summary

Differentiability of a Function: A function $f (x)$ $f(x)$ is differentiable at point $x = a$ $x=a$ if the derivative-limit is defined. That is,
right-hand-limit $lim_{x \to a +} \frac{f (x) - f (a)}{x - a}$ $lim_(x->a+) (f(x)-f(a))/(x-a)$ and left hand limit $lim_{x \to a -} \frac{f (x) - f (a)}{x - a}$ $lim_(x->a-) (f(x)-f(a))/(x-a)$ are equal and evaluates to a real value.

A function is differentiable at a point, if the instantaneous rate of change at that point is continuous.

A function is continuously differentiable, if the instantaneous rate of change is continuous for any and all points from $- \infty \to + \infty$ $-oo to +oo$

A function is continuously differentiable in a range `a
The instantaneous rate of change or the derivative-limit is given as
$lim_{δ \to 0} \frac{f (x + δ) - f (x)}{δ}$ $lim_(delta->0) (f(x+delta) - f(x))/delta$ .

Outline

The outline of material to learn "Differential Calculus" is as follows.

• Detailed outline of Differential Calculus

→ Application Scenario

→ Differentiation in First Principles

→ Graphical Meaning of Differentiation

→ Differntiability

→ Algebra of Derivatives

→ Standard Results