Differential Calculus

maths

The differentiation or derivative calculus is explained in astonishingly simple and clear thought process. The differentiation is covered in the following topics.

• application scenario of differentiation

• first principles of differentiation

• graphical meaning of derivatives

• differentiability of a function

• algebra of derivatives

• standard results in derivatives

The details explained are ingenious and found nowhere else.

maths > differential-calculus > differentiation-application-scenario

Differential Calculus : Understanding Application Scenarios

In this page, the application scenario of derivatives is explained with examples. We consider pair of related quantities. One quantity is the cause and the other is the effect. These are related by a function involving instentaneous rate of change.

maths > differential-calculus > differentiation-first-principles

Differentiation: First Principles

In this page, differentiation is defined in first principles : instantaneous rate of change is the change in a quantity for a small change $δ \to 0$ $delta->0$ in the variable.

Derivative or Differentiation of a function

For a small change in variable $x$ $x$ , the rate of change in the function $f (x)$ $f(x)$ is the derivative of the function.

$\frac{d}{d x} f (x)$ $d/(dx) f(x)$

$= f' (x)$ $= f′(x)$

$= lim_{δ \to 0} \frac{f (x + δ) - f (x)}{δ}$ $= lim_(delta->0) (f(x+delta) - f(x))/delta$

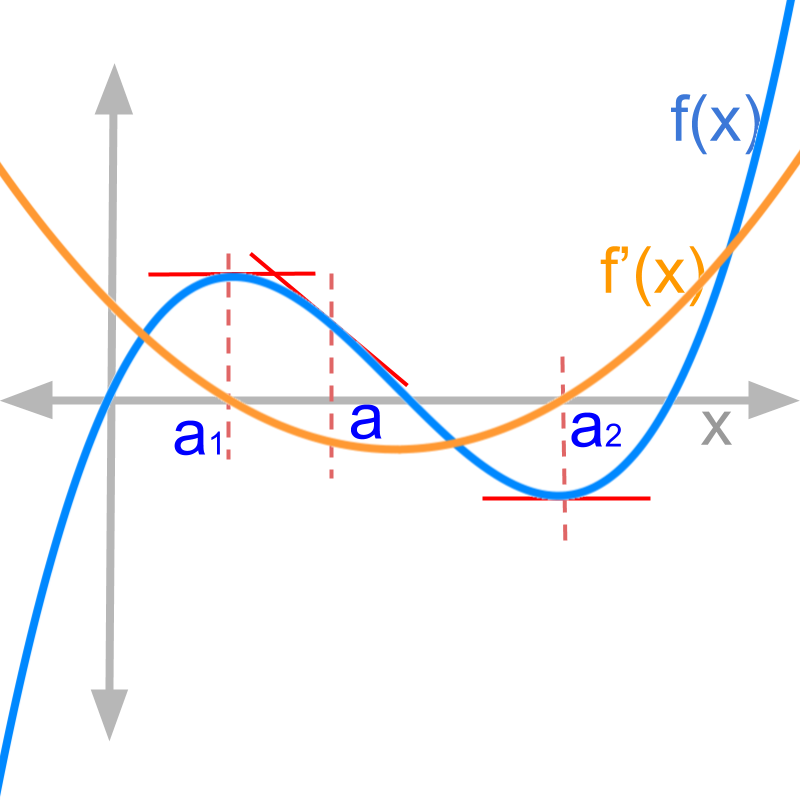
maths > differential-calculus > differentiation-graphical-meaning

Differentiation: Graphical Meaning

In this page, graphical meaning of differentiation is discussed with examples: derivative of a function at a point is the slope of tangent at that point. derivative reference

maths > differential-calculus > differentiation-differentiability

Differentiability of Functions

In this page, the conditions under which derivative is defined for functions is discussed.

A function is differentiable at a point, if the instantaneous rate of change at that point is continuous.

A function is continuously differentiable, if the instantaneous rate of change is continuous for any and all points from $- \infty \to + \infty$ $-oo to +oo$

A function is continuously differentiable in a range `a

maths > differential-calculus > differentiation-algebra-of-derivatives

Understanding Algebra of Derivatives

In this page, what is algebra of derivatives and conditions under which it is applicable are discussed. Then the derivatives of functions that are given as arithmetic operation of multiple functions is discussed. The arithmetic operations are addition, subtraction, multiplication, and division. The derivatives of functions in composite form and parametric forms are discussed.

Differentiation under Basic Arithmetic Operations

    → $(a u)' = a u'$ $(a u)′ = a u′$

    → $(u + v)' = u' + v'$ $(u+v)′ = u′ + v′$

    → $(u - v)' = u' - v'$ $(u-v)′ = u′ - v′$

    → $(u v)' = u' v + u v'$ $(uv)′=u′v+u v′$

    → $(\frac{u}{v})' = \frac{u' v - u v'}{v^{2}}$ $(u/v)′=(u′v-u v′)/(v^2)$

» Differentiation under Function Operations

    → Composite form and Chain rule: given $v (u)$ $v(u)$ and $u (x)$ $u(x)$ (i.e. $v (u (x))$ $v(u(x))$ ) then
$\frac{d v}{d x} = \frac{d v}{d u} \frac{d u}{d x}$ $(dv)/(dx) = (dv)/(du)(du)/(dx)$

    → Parametric form : given $g (x)$ $g(x)$ and $h (x)$ $h(x)$ then
$\frac{d g}{d h} = \frac{d g / d x}{d h / d x}$ $(dg)/(dh) = (dg//dx)/(dh//dx)$

maths > differential-calculus > differentiation-standard-results

Derivatives of Algebraic Expressions

In this page, Derivatives of standard functions in algebraic expressions are explained. Then the derivatives of trigonometric functions sin, cos, tan etc. are discussed. Then the derivatives of inverse trigonometric functions such as $\arcsin$ $arcsin$ , $\arccos$ $arccos$ , etc. are discussed. Then the derivatives of exponents and logarithmic functions such as $e^{x}$ $e^x$ , $a^{x}$ $a^x$ , and $\ln x$ $ln x$