Algebra : Foundation with Numerical Arithmetics : Laws and Properties of Arithmetics : Comparison

maths > algebra

Laws and Properties of Arithmetics : Comparison

what you'll learn...

Overview

Comparison

» Trichotomy Property
"tri-" means three and "-chotomy" means division-into-parts.
    → Given $a, b \in ℝ$ $a,b in RR$ one and only one of the following is true.
      $a < b$ $a<b$
      $a = b$ $a=b$
      $a > b$ $a>b$

» Transitivity
"trans-" means across and "-itivity" means to-go or to-pass
    → If $a = b$ $a=b$ and $b = c$ $b=c$ , then it implies $a = c$ $a=c$
    → If $a < b$ $a<b$ and $b < c$ $b<c$ , then it implies $a < c$ $a<c$
    → If $a > b$ $a>b$ and $b > c$ $b>c$ , then it implies $a > c$ $a>c$

three possibilities

Given two real numbers $p$ $p$ and $q$ $q$ , which of the following is correct?

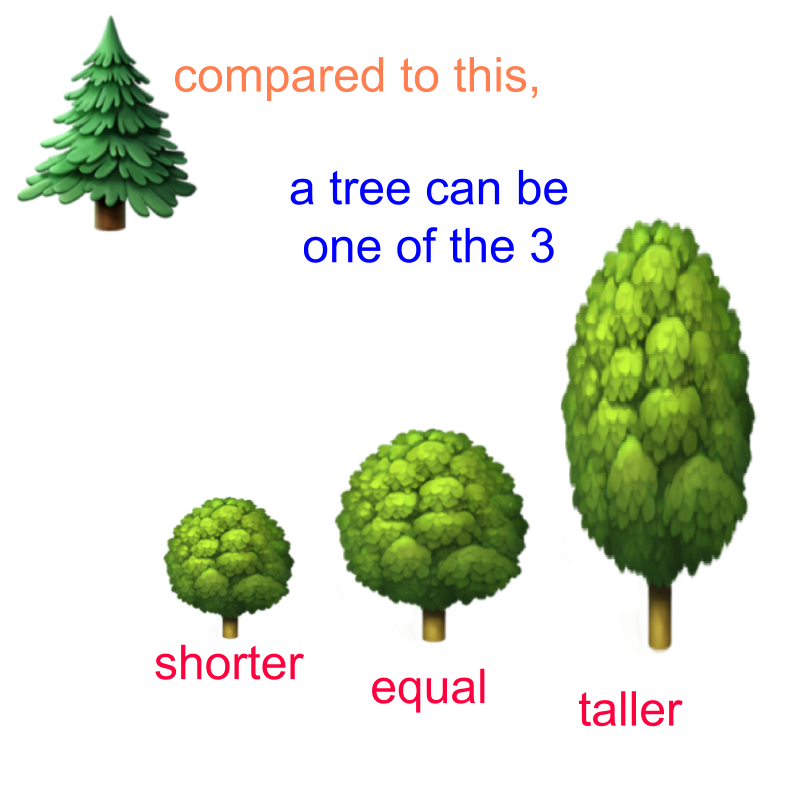
Trichotomy Property: For any numbers $p, q \in ℝ$ $p,q in RR$ , one and only one of the following is true.
$p < q$ $p<q$
$p = q$ $p=q$
$p > q$ $p>q$

Note: sometimes, $p \leq q$ $p<=q$ is considered. This specifies, consider pair of numbers $p$ $p$ and $q$ $q$ such that $p$ $p$ is less than or equal to $q$ $q$ .

It specifies which numbers to choose. That is, if $q$ $q$ is 4, then $p$ $p$ can be any negative number or $0, 1, 2, 3, 4$ $0, 1, 2, 3, 4$ . It defines a set of numbers for $p$ $p$ .

In trichotomy property, for any two numbers (for example, $4$ $4$ and $3$ $3$ ), one and only one of the three possibilities is true.

The word "trichotomy" means: Division into three parts.

tri- means three and -chotomy means division-into-parts

pass across

For three real numbers $p, q, r$ $p,q,r$ , it is given that $p < q$ $p<q$ and $q < r$ $q<r$ , then $p < r$ $p<r$

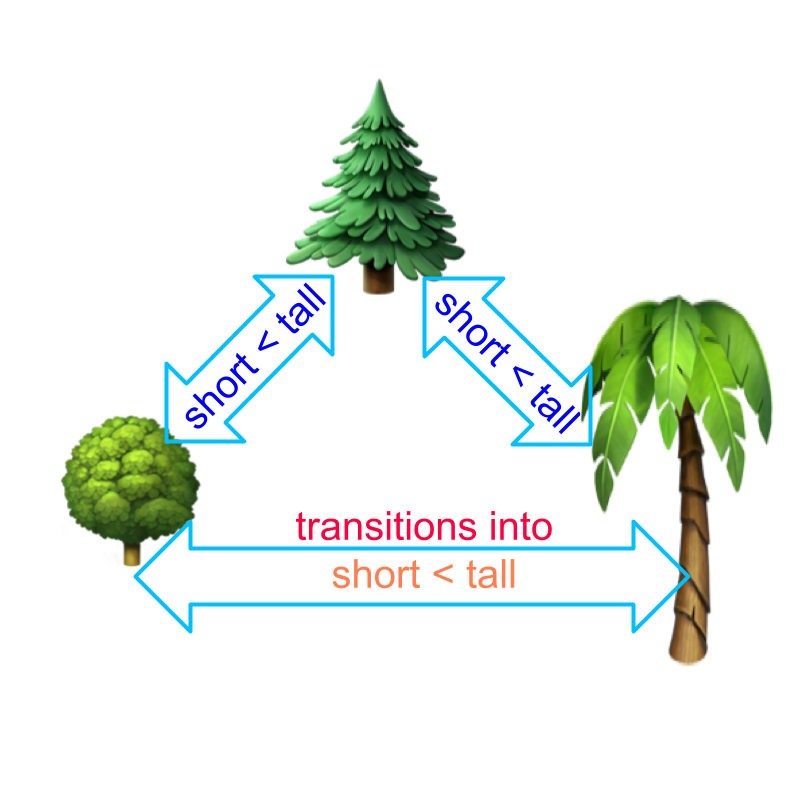
Transitivity Property: For three numbers $p, q, r \in ℝ$ $p,q,r in RR$ ,

• if $p < q$ $p<q$ and $q < r$ $q<r$ , then $p < r$ $p<r$ .

• if $p = q$ $p=q$ and $q = r$ $q=r$ , then $p = r$ $p=r$ .

• if $p > q$ $p>q$ and $q > r$ $q>r$ , then $p > r$ $p>r$ .

Note 1: If $p < q$ $p<q$ and $q > r$ $q>r$ , then the relation between $p$ $p$ and $r$ $r$ cannot be ascertained.

Note 2: If $p < q$ $p<q$ and $q = r$ $q=r$ , then $q$ $q$ can be replaced by $r$ $r$ to get $p < r$ $p<r$ .

The word "transitivity" means: some property passes across from one to another.

trans- means across and -itivity means to-go or to-pass.

summary

LPA - Comparison : Comparison of numbers has Trichotomy and Transitivity properties.

» Trichotomy Property
"tri-" means three and "-chotomy" means division-into-parts.
    → Given $a, b \in ℝ$ $a,b in RR$ one and only one of the following is true.
      $a < b$ $a<b$
      $a = b$ $a=b$
      $a > b$ $a>b$

» Transitivity Property
"trans-" means across and "-itivity" means to-go or to-pass
    → If $a = b$ $a=b$ and $b = c$ $b=c$ , then it implies $a = c$ $a=c$
    → If $a < b$ $a<b$ and $b < c$ $b<c$ , then it implies $a < c$ $a<c$
    → If $a > b$ $a>b$ and $b > c$ $b>c$ , then it implies $a > c$ $a>c$

Outline

The outline of material to learn "Algebra Foundation" is as follows.

Note: click here for detailed outline of Foundation of Algebra

→ Numerical Arithmetics

→ Arithmetic Operations and Precedence

→ Properties of Comparison

→ Properties of Addition

→ Properties of Multiplication

→ Properties of Exponents

→ Algebraic Expressions

→ Algebraic Equations

→ Algebraic Identities

→ Algebraic Inequations

→ Brief about Algebra