Algebra : Foundation with Numerical Arithmetics : Laws and Properties of Arithmetics : Addition

maths > algebra

Laws and Properties of Arithmetics : Addition

what you'll learn...

Overview

CADI Properties of Addition

» Closure Property
    → if $x, y \in ℝ$ $x,y in RR$ , then $x + y \in ℝ$ $x+y in RR$

» Commutative Property
    → $x + y = y + x$ $x+y = y+x$

» Associative Property
    → $(x + y) + z = x + (y + z)$ $(x+y)+z = x+(y+z)$

» Additive Identity Property
    → $0 \in ℝ$ $0 in RR$ , such that $x + 0 = x$ $x+0 = x$

» Additive Inverse Property
    → $- x \in ℝ$ $-x in RR$ for any $x \in ℝ$ $x in RR$ such that $x + (- x) = 0$ $x+(-x) = 0$

» Subtraction is to be handled as additive inverse for the properties
this is important as algebra extensively involves these properties
    → Commutative property involving subtraction : $x - y$ $x-y$ is given as $x + (- y) = (- y) + x$ $x+(-y) = (-y) + x$
    → Associative property involving subtraction : $(x - y) - z$ $(x-y)-z$ is given as $(x + (- y)) + (- z) = x + ((- y) + (- z))$ $(x+ (-y))+(-z) = x+ ((-y)+(-z))$

closed means within

Consider the numbers $2$ $2$ and $3$ $3$ . Is $2 + 3$ $2+3$ a real number? "yes, a real number".

That is, for any real numbers $p, q$ $p,q$ , $p + q$ $p+q$ is always a real number

"closure" means closed and not open

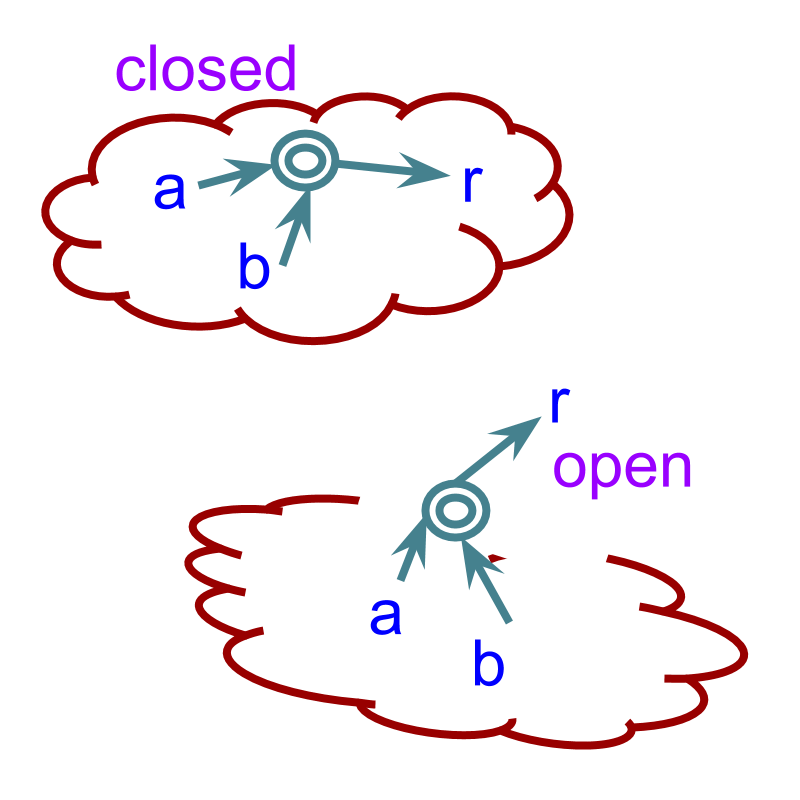
Closure Property of Addition: Given $p, q \in ℝ$ $p,q in RR$ , $p + q \in ℝ$ $p+q in RR$ .

Closure Property applied to Subtraction: Given $p, q \in ℝ$ $p,q in RR$ . $p - q \in ℝ$ $p-q in RR$ .

Proof:
Given $p, q \in ℝ$ $p,q in RR$
$- q \in ℝ$ $-q in RR$ as per Additive Inverse Property
$p + (- q) \in ℝ$ $p+(-q) in RR$ as per Closure property of Addition
$\Rightarrow p - q \in ℝ$ $=> p-q in RR$

Using Closure Property: Given $p, q, r, s \in ℝ$ $p,q,r,s in RR$ , $p + q - r + s$ $p+q-r+s$ , the subexpression $p + q - r$ $p+q-r$ is a real number and can be considered as a single number for any other property.

For example as per commutative property $p + q - r + s = s + p + q - r$ $p+q-r+s = s+p+q-r$ , in which $p + q - r$ $p+q-r$ is considered to be a single real number.

Consider the numbers $2$ $2$ and $3$ $3$ . Which of the following is true?
$2 + 3 = 3 + 2$ $2+3 = 3+2$ or
$3 + 2$ $3+2$ does not equal to $2 + 3$ $2+3$

The answer is " $2 + 3 = 3 + 2$ $2+3 = 3+2$ ".

Given $p, q \in ℝ$ $p,q in RR$ ; $p + q = q + p$ $p+q = q+p$

forward and backward

The word "commute" means "to go to and fro between two places on a regular basis".

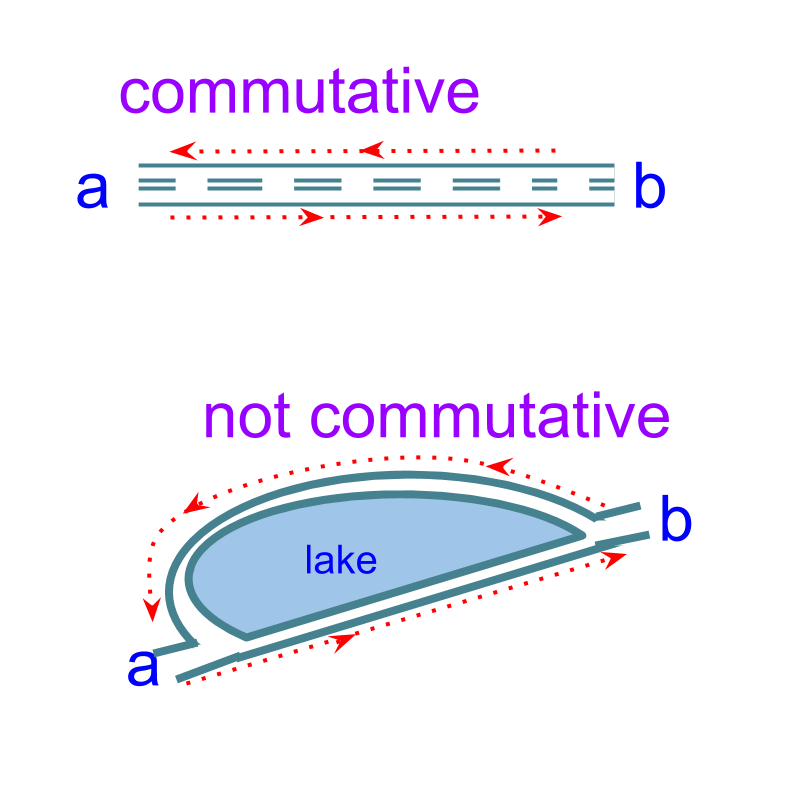
Commutative Property of Addition: Given $p, q \in ℝ$ $p,q in RR$ , $p + q = q + p$ $p+q=q+p$ .

Commutative Property applied to Subtraction: $p - q = - q + p$ $p-q=-q+p$ .
Note: Subtraction has to be handled as inverse of addition, $p - q = p + (- q)$ $p-q = p+(-q)$ and then commutative property can be used.

Using Commutative Property: Given $p, q, r \in ℝ$ $p,q,r in RR$ , the expression $p + q + p - q + r - p + 2 r$ $p+q+p-q+r-p+2r$ is simplified to $p + 3 r$ $p+3r$ . students may work this out to understand.

with this or that

Given $p, q, r \in ℝ$ $p,q,r in RR$ . The expression $(p + q) + r$ $(p+q)+r$ equals $p + (q + r)$ $p+(q+r)$

In the first expression, $q$ $q$ is added first with $p$ $p$ and then $r$ $r$ is added to the result.
In the second expression $q$ $q$ is added first with $r$ $r$ and then $p$ $p$ is added to the result.
Either way, the result is same.

For example, $(2 + 3) + 7 = 2 + (3 + 7)$ $(2+3)+7 = 2+(3+7)$

The word "associate" means 'to connect with; to join'.

Associative Property of Addition: Given $p, q, r \in ℝ$ $p,q,r in RR$ . $(p + q) + r = p + (q + r)$ $(p+q)+r = p+(q+r)$ .

Associative Property applied to subtraction: $(p - q) - r = p + (- q - r)$ $(p-q)-r = p+(-q-r)$ .
Note: Subtraction has to be handled as inverse of addition, $(p - q) - r = (p + (- q)) + (- r)$ $(p-q)-r = (p+(-q))+(-r)$ and then associative property can be used.

zero

Given $p \in ℝ$ $p in RR$ . What is $p + 0 = p$ $p+0 = p$

Additive Identity Property: For any $p \in ℝ$ $p in RR$ , there exists $0 \in ℝ$ $0 in RR$ such that $p + 0 = p$ $p+0=p$ . Additive Identity applied to Subtraction: $p - 0 = p$ $p-0 = p$

Note: $- 0 = 0$ $-0=0$ and so $p - 0 = p + (- 0) = p + 0 = p$ $p-0=p+(-0)=p+0 = p$ .

inverse

Given $p \in ℝ$ $p in RR$ . What is $p - p = 0$ $p-p = 0$

Additive Inverse Property: For any $p \in ℝ$ $p in RR$ , there exists $- p \in ℝ$ $-p in RR$ such that $p + (- p) = 0$ $p+(-p)=0$ .

summary

The properties together are named as CADI properties of addition. The abbreviation CADI is a simplified form of the first letters of Closure, Commutative, Associative, Distributive, Inverse, and Identity properties.

Note: Distributive property is shared with multiplication and is explained in the next page.

LPA: CADI properties of Addition
• Closure Property
      if $x, y \in ℝ$ $x,y in RR$ , then $x + y \in ℝ$ $x+y in RR$

• Commutative Property
      $x + y = y + x$ $x+y = y+x$

• Associative Property
      $(x + y) + z = x + (y + z)$ $(x+y)+z = x+(y+z)$

• Additive Identity Property
      $0 \in ℝ$ $0 in RR$ , such that $x + 0 = x$ $x+0 = x$

• Additive Inverse Property
      $- x \in ℝ$ $-x in RR$ for any $x \in ℝ$ $x in RR$ such that $x + (- x) = 0$ $x+(-x) = 0$

Subtraction is to be handled as additive inverse and properties of addition applies to subtraction in the form of addition.

This is important as algebra extensively uses these properties.

→ Commutative property involving subtraction : $x - y$ $x-y$ is given as $x + (- y)$ $x+(-y)$ $= (- y) + x$ $= (-y) + x$
→ Associative property involving subtraction : $(x - y) - z$ $(x-y)-z$ is given as $(x + (- y)) + (- z)$ $(x+ (-y))+(-z)$ $= x + ((- y) + (- z))$ $= x+ ((-y)+(-z))$

Outline

The outline of material to learn "Algebra Foundation" is as follows.

Note: click here for detailed outline of Foundation of Algebra

→ Numerical Arithmetics

→ Arithmetic Operations and Precedence

→ Properties of Comparison

→ Properties of Addition

→ Properties of Multiplication

→ Properties of Exponents

→ Algebraic Expressions

→ Algebraic Equations

→ Algebraic Identities

→ Algebraic Inequations

→ Brief about Algebra